Published online Apr 14, 2006. doi: 10.3748/wjg.v12.i14.2187
Revised: July 1, 2005
Accepted: August 26, 2005
Published online: April 14, 2006
AIM: To provide the accurate alternative metrical means of monitoring the effects of new antiviral drugs on the reversal of newly formed collagen.
METHODS: Digitized histological biopsy sections taken from 209 patients with chronic C virus hepatitis with different grade of fibrosis or cirrhosis, were measured by means of a new, rapid, user-friendly, fully computer-aided method based on the international system meter rectified using fractal principles.
RESULTS: The following were described: geometric perimeter, area and wrinkledness of fibrosis; the collation of the Knodell, Sheuer, Ishak and METAVIR scores with fractal-rectified metric measurements; the meaning of the physical composition of fibrosis in relation to the magnitude of collagen islets; the intra- and inter-biopsy sample variability of these parameters; the “staging” of biopsy sections indicating the pathway covered by fibrosis formation towards its maximum known value; the quantitative liver tissue architectural changes with the Hurst exponent.
CONCLUSION: Our model provides the first metrical evaluations of the geometric properties of fibrosis and the quantitative architectural changes of the liver tissue. The representativeness of histological sections of the whole liver is also discussed in the light of the results obtained with the Hurst coefficient.
- Citation: Dioguardi N, Grizzi F, Franceschini B, Bossi P, Russo C. Liver fibrosis and tissue architectural change measurement using fractal-rectified metrics and Hurst’s exponent. World J Gastroenterol 2006; 12(14): 2187-2194
- URL: https://www.wjgnet.com/1007-9327/full/v12/i14/2187.htm
- DOI: https://dx.doi.org/10.3748/wjg.v12.i14.2187
Experimental medical research based on reductionism retains in principle that the causes governing the processes and controls of the formation, growth and behavioral dynamics of living beings at macro-scalar levels can be derived from the processes and controls that take place at micro-scalar level.
This conception has led the hepatological disciplines to seek exact quantitative descriptions of the contents of liver fibrosis on the basis of the blood molecules related to the presence of the newly formed structure[1-5]. The basic idea is that the laws governing the set of processes and controls acting at the scale of the formation of septal and anular collagen structures can be translated into the set of laws that regulate the dynamics of these molecules at micro-scalar level when they enter the blood stream.
Sophisticated mathematical, physical and environmental studies suggest that these phenomena are governed by different multiple processes and controls (causality) at every larger or smaller scale rather than that of observation. The set of these multiple processes and controls is known as multiple scale causality (MSC)[6]. The macro-scalar growth of liver collagen fibres evolving into the septa and annuli of fibrosis is regulated by the physical events of diffusion, percolation, stratification and contraction of the extra-cellular matrix (ECM), and by the processes of neo-vascularisation. These physical processes are not involved in generation of microfibrils and fibrils, which is limited on ECM deposition. This phenomenon depends on the relationships between the processes of collagen synthesis and lyses, which are different from the biochemical processes that at a lower scale, regulate the quantitative and qualitative behaviors of the molecules formed during fibrogenesis and found in circulating blood. In other words, this means “what happens in the test tubes may be the same, the opposite, or bear no relationship at all to what happens in the living cells, still less the living organisms”.
In brief, the MSC-based conception rejects the idea that the laws regulating phenomena at one scale can in principle be derived from those regulating phenomena at a lower scale. In other words, every scale is characterized by different degrees of entropy[6].
As the characteristics of MSC are not universal, it is almost always impossible to establish a strict connection between the phases leading an observed object from micro- to macro-scalar positions and vice versa. Consequently, it is very difficult to identify a one-to-one relationship between the macro- and micro-scalar processes and controls of liver fibrosis production.
These considerations have convinced us to improve a direct, rapid and friendly method of measuring fibrosis using a meter that is suitable for its naturally irregular shape, provided that the biopsy procedures are performed by experts[7-12].
Liver biopsy is the only direct means of discovering the changes in liver tissue induced by chronic B or C virus-dependent inflammation and the fibrosis it causes[12-17]. Although it is the canonical point of reference for establishing the progression of the process, fibrosis has so far only been estimated on the basis of semi-quantitative evaluations[18-21] or morphometric methods[22-26] that must be considered approximate because of their use of the international system (IS) meter, which is unsuitable for measuring irregular shapes[7-11].
Like all natural objects, the collagen islets making up the fibrosis appear to be difficult to measure at all degrees of magnification because of their highly irregular shapes[7-11]. Furthermore, they do not have a single measurement because, at each enlargement (scale), their shape changes as a result of the addition of new details which are imperceptible at smaller scales. Mandelbrot have termed these irregular bodies fractal objects[27].
The studies of Perrin[28] in 1906, Hausdorff[29] in 1919, Richardson[30] in the 1950s, and Mandelbrot et al[26] in the 1970s and 1980s suggested a new geometry that has made it possible to measure such objects using a method that can be made simple with aid of computer technology.
The aim of this paper was to present the first results of the quantitative analysis of histological liver bioptical sections made using new metrics suggested by the concepts of fractal theory.
Our contribution to the quantitative evaluation of fibrosis in liver biopsies concerns: (1) the closest to real metric estimate of the surfaces covered by fibrosis and the quantitative classification of collagen islets; (2) the collation of metric and traditional semi-quantitative evaluations of collagen area; (3) considerations concerning the relationships depending on specific estimates defined by real numbers as a means of identifying the stadium of fibrosis; (4) the interior-to-edge metric relationship of the collagen islets used as an index of wrinkledness; (5) the definition of the harmonic state of the architectural structure of liver tissue, and the recognition and classification of its disharmonic states or architectural disorder using Hurst’s exponent; (6) the intra-sample variability of fibrosis (area, wrinkledness and Hurst’s exponent); and (7) the variability of the latter parameters in eight samples taken from the explanted liver of a transplant patient.
Characteristics of collagen islets The spaces occupied by the collagen islets making up fibrosis (Figure 1), and those occupied by the surviving fragments of parenchymal tissue, are both characterized by irregular shapes that exclude them from the application of Euclidean geometry[7-11]. However, their configurations make them members of the family of asymptotic statistical fractals (also called truncated fractals as they cannot be endlessly fracted)[31].
Dimension The dimension of an object indicates the Euclidean space it occupies. The fractionable “smooth” objects of classic geometry (a point, straight line, plane, and solid figure) occupy spaces whose dimensions are expressed by the whole numbers zo, 1, 2 and 3, whereas the irregular objects that are frangible into irregular pieces (sets of points, broken lines, undulating planes and irregular solids) occupy the intermediate spaces, and therefore have dimensions that cannot be expressed by whole numbers. In 1977, Mandelbrot[27] defined the objects whose dimensions are denoted by non-whole numbers as “fractals”. The fractal dimension is indicated by D, and the Euclidean (or topological) dimension by Dγ.
Harmonic state of liver tissue The use of an analytical method based on a new geometry requires a brief formal description of the natural history of chronic virus-related hepatitis starting from the axiom that is defined by the persistence of a discreet necro-inflammatory process maintaining the activity of the ECM→collagen→fibrosis production system. The growth of fibrosis interrupts the continuity of the parenchyma, dissects it into irregular pieces, and compresses and atrophies the pieces enclosed in the fibrotic mass. This has two consequences: 1) it disrupts the natural harmonic state of the metric spaces covered by both natural fibrosis and the parenchyma, and 2) it alters the typical lobular architecture of hepatic tissue.
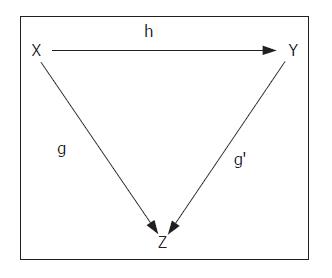
Using these axioms, the process can be represented by the first-order general equation:
z = f(x, y)1)
in which z denotes the harmony of the natural architecture of liver tissue, x the metric space covered by fibrosis, and y the metric space covered by the parenchyma. The relationship of z to x and y can be indicated by the categorial representation (Figure 2), which shows the dependence of the state of z on the extension over z of the relationships between the “objects over” indicated by x and y in f(x→y).
As the variations in x and y are interconnected by the equality (z-x)+(z-y)=1, we can consider x and y as complementary spaces, and so the expression z = f(x→y) can be simplified to the form z = f(x). The harmony of natural architecture of liver tissue is characterized by 3% fibrosis and 97% lobular parenchyma[32].
The evaluation of the metric space covered by the fibrosis induced by pathogenic agents is therefore sufficient by itself to describe the variations in the harmonic state of liver tissue architecture.
An alteration in the natural quantitative relationship between fibrosis and the parenchyma leads to the loss of the natural lobular architecture of hepatic tissue in a continuous but irregular progression that fractal geometry calls a random walk, or Brownian process[33,34].
Two hundred and seven consecutive needle biopsy specimens (≥10 mm long) were taken from 74 female and 135 male patients (mean age: 52 ± 13 years) with chronic C virus-related liver disease. To evaluate the inter-sample variability of geometric characteristics of fibrosis, a total of six biopsy specimens were sampled from a liver explanted from a patient with clinically and histologically proved cirrhosis undergoing orthotopic liver transplantation. Each biopsy specimen was taken from a single segment of the liver.
The study was performed in accordance with the guidelines of the Ethics Committee of the Istituto Clinico Humanitas, Rozzano and Ospedale Maggiore, Milan, Italy. All the patients were informed of the possible discomforts and risks of bioptic sampling. The liver specimens were fixed in 10% formalin and embedded in paraffin, and 2 μm thick sections were cut and stained with a freshly made 0.1% Sirius red staining solution[35].
At least three expert pathologists independently staged the biopsies using Knodell’s histology activity index (HAI), and the Sheuher, Ishak and METAVIR scoring systems. The number of available portal tracts in the liver fragment was assured on the basis of the indications established for the individual methods[18-21].
Our specially developed computer program could ensure: computer-driven microscopy focusing, digitation of the whole histological section and its fractal dimension and Hurst’s exponent, less-biased measurements of each collagen islet and fibrosis mass raster perimeter length and area magnitude corrected by the fractal dimension, and wrinkledness of the fibrosis[7-11]. The time required for the whole analytical operation using this software was 30 s/mm2, as determined on a standard reference needle specimen section, and was carried out at a microscopic magnification of ×200 (the measurements were valid only for that scale). The observed objects were measured using the IS meter rectified by their fractal dimension. When present, Glisson’s capsule was included in the physiological amount of ECM, which was estimated as being 3% of the true area of the section[32].
The fractal dimensions were automatically estimated using the box-counting method and the formula 2)
in which, DB is the box-counting fractal dimension of the object, ε the side length of the box, and N(ε) the smallest number of boxes of side ε required to cover the surface or the outline of the object completely[7-11,33,34]. As the zero limit could not be applied to biological objects, the dimensions were calculated as D = d, where d is the slope of the graph of log [N(ε)] against log 1/ε. The log-log graphs were plotted, and the linear segments were identified using least squares regression. Their gradients were calculated using an iterative resistant line method.
Hurst’s exponent, which gives a measure of the heterogeneous distribution of a set of irregularly-shaped objects[36-38], was obtained using the general relationship:
H = E +1 - D 3)
where E indicates the Euclidean topological dimension, and D the fractal dimension of the surface covered by the extensions of all the collagen islets making-up the fibrosis. This exponent is capable of evaluating the loss of natural order that occurs in the histological picture as a result of the disruption of the natural quantitative relationship between the metric spaces covered by fibrosis and the parenchyma[11]. This could give the alterations the significance of a physical variable, make Hurst’s exponent the descriptor of the configurational disorder of the hepatic tissue, and leave the fractal dimensions of the collagen islets and fibrosis the significance of an evaluation of how “densely” they occupy the metric space in which they lie and their spatial position.
In brief, Hurst's exponent values near to 1 quantitatively indicate a large loss of architectural harmony in the system (i.e. disordered states), whereas values near to zero indicate its preservation (i.e. states of structural order).
The reduction in Hurst’s exponent could also be interpreted as an index of the limited stability of a fractal object progressing towards more advanced states of stability.
The construction of a meter with the most favorable spatial dimension for measuring the perimeter and area of the collagen islets was based on the assumptions that broken or mixed (in any case irregular) lines could be described as a “dilatative” (expanded) state of a straight line, and that their irregularity could be measured using the fractal dimension with similar criteria to those with which the coefficient of dilatation (λ) could be used to describe the length of a linear object before (s) and after (S) its exposure to the effect of heat expressed in the following formula:
S = s (1+λt) 4)
where t is the duration of heat exposure[10].
According to this principle (which has been discussed elsewhere), the meter suitable for measuring a fractal object (mF) could be obtained using the formula:
mF = m [1 + β (DP-Dγ)] 5)
in which, mF indicates the rectified meter, m the IS meter, β the dilatation constant of the unit of measure, DP the fractal dimension of the perimeter, and Dγ the topological or Euclidean dimension[10]. The metric perimeter and area measurements were detected using the true liver biopsy area (indicated by the symbol AB), by which we meant the surface area excluding any vascular, bile channel, sinusoidal or other empty spaces created by tissue loss during specimen manipulations.
All the data were expressed as mean±SD. The linear regression analysis was made using Spearman’s correlation and Student’s t test with Statistica software (StatSoft Inc., Tulsa, OK, USA). P < 0.05 was considered statistically significant. The degree of intra- and inter-sample variability was quantitatively evaluated using the coefficient of variation (CV) given by the formula CV = SD/mean. Quantitative measures of fibrosis surfaces were compared (collated) with those of the score categories of the four currently used semi-quantitative methods.
By evaluating this parameter in our case-list of patients with chronic C virus-related hepatitis, we obtained dimensional values (D) ranging from 1.22 to 1.79. The value of this parameter increased depending on the extension of the fibrosis, with a regression curve ratio of r = 0.81.
The fibrosis perimeter (PC) defined the sum of the perimeters all of the Sirius Red-stained areas of collagen in each biopsy section measured using the IS meter. The fractal fibrosis perimeter (PCF) defined the same sum of perimeters measured using the fractal-rectified meter. The mean PC was 860.64 ± 588 μm, and the mean PCF was 2966.1 ± 2304.4 μm (P < 0.0005). The marked difference Δ was 225.21 ± 38.69% due to the rectification, which included most of the fine, irregular particulars escaping the IS meter, thus making the result very close to reality. In this study, we only used the measurements corrected using the fractal dimension. The scalars indicating the length of the perimeters of fibrosis in each of the sections of the 209 bioptic samples fell within a range that was only closed at the zero point because the maximum value was not defined and could theoretically be greater.
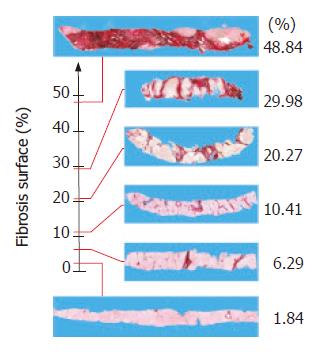
The area of fibrosis (AC) defined the sum of the areas of the Sirius Red-stained collagen islets measured using the IS meter. The fractal area of fibrosis (ACF) was the sum of the areas of Sirius Red-stained collagen islets measured using the fractal-rectified meter. Both were expressed as a percentage of the total true area. The minimum and maximum values of AC were 1.01% and 48.47% of the specimen area, the corresponding ACF values were 1.34% and 48.84%. In this case, although statistically significant (P < 0.005), the Δ(6.61%±4.79%) was small because histological sections were planar and the fractal measure of area depended only on its irregular contour. The scalars indicating the extent of the area of fibrosis in each of the sections of the 209 bioptic samples also fell within a range that was only closed at the zero point because the maximum value was not yet defined and could theoretically be greater.
We constructed a geometrical model of the set of all states of ECM deposition on the line of real numbers as their state space using the scalars obtained from the fibrosis measured in our biopsies. The α (start) of the fibrotic process was fixed at 0% and the ω (end) at 48.84% of the area of the section (Figure 3). This model could represent a conventional interpretation of the ideal path that could be covered by potential fibrosis deposition in liver tissue. The staging observed in the histological section under examination was given by the relationship between the scalar expressing the actual fibrotic state of the section and the point indicated by this geometric model.
During the course of chronic hepatitis, fibrosis appeared under the control of stellate cells in the form of thin fibers that tended to grow in width and length within the portal space, around these structures and the central veins, and along the capillarised sinusoidal network. The three-dimensional interconnections of these collagen structures led to the formation of a fibrous network in which irregular meshes appeared as a set of collagen islets on different magnitudes on planar histological sections.
The logarithmic distribution of this set of 2.8 million collagen islets from 209 cases showed that it could be divided into three classes of elements of different magnitude: the collagen islets of 10-103μm2, those of between 103 and 104μm2, and those between 104 and 106μm2. All the histological sections contained islets with these classes of metrical values. In order to clarify the meaning of their presence, we first ordered the results of the fibrosis surface areas and constructed them in function of their magnitude as a Markovian curve (Figure 4).
The values of the islets belonging to the three subclasses in each bioptic section were plotted on the basis of the order of a Markovian curve, which generated the three irregular curves formed by the sets of islets belonging to each subclass. The fractal dimension of these curves showed that the Markovian reference curve had a fractal dimension of 1.1, whereas the curves of the three subclasses of the largest, medium-sized and smallest islets were respectively 1.9, 1.99 and 1.95. Fractal geometry suggested that the high fractal dimensions of the collagen islet subclasses could describe the instability of the collagen structure as it passed towards more stable fibrotic states[33].
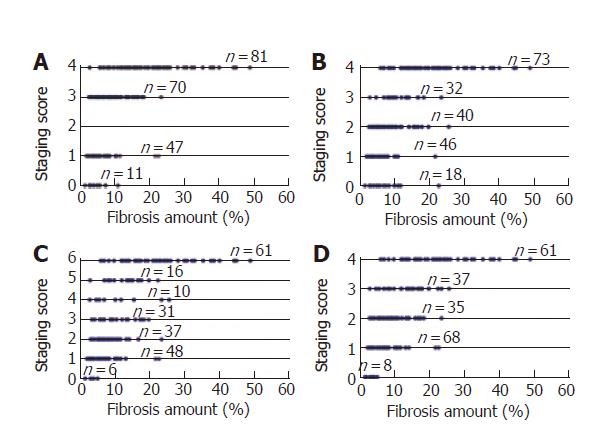
The relationships between our measurements of fibrosis, the semi-quantitative Knodell histology activity index, and Sheuer, Ishak and METAVIR scores were investigated by comparing the portraits of each category of elements obtained by labeling the different semi-quantitative values on a geometric model using the line of real numbers as state space (Figure 5). The overlapping metric measures showed that samples with very similar metric surface areas fell into different categories while specimens with different metric surface areas fell into similar categories. Incidentally, our results reinforced the criticism by Rousselet et al[39] who have recently criticized the METAVIR system for evaluating fibrosis.
Wrinkledness (W), a typical characteristic of all natural fractal objects[11], could be obtained using the formula:
W = PCF - R 6)
where R is the roundness coefficient of each islet.
The mean W value obtained by measuring the 209 biopsy sections was 731.3±298.72. As expected, this variable did not depend on the area of collagen (r = 0.14), but was highly dependent on the length of its perimeter (r = 0.80). Preliminary data showed that W was independent of the degree of necro-inflammatory activity (data not shown).
The same 209 patients provided us with H values ranging from 0.21 and 0.71. As said in the premises, we considered this index a quantitative variable of the alteration in hepatic tissue architecture. The ratio between H and the extension of the area of fibrosis indicated that the increased fibrotic area could lead to an extended loss of the natural harmony of this architecture (r = -0.81).
In order to define the usefulness of generating numbers (or other kinds of invariants) to label the investigated structures in such a way that those with the same label could be considered alike and those with different labels could be considered different, the irregular tectonics of fibrosis was investigated in 30 sections taken at equal intervals from two patients with different degrees of disease severity and one was considered normal. The data (Table 1) showed the highly multifarious areas and wrinkledness of the collagen islets in the different sections. However, the Hurst’s exponent was found less variable.
| Patient number | n | ACF(%) | CV | W | CV | H | CV |
| 1 | 30 | 5.97 ± 4.95 | 0.83 | 788.63 ± 590.48 | 0.75 | 0.51 ± 0.14 | 0.27 |
| 2 | 30 | 9.77 ± 2.64 | 0.27 | 830.52 ± 124.93 | 0.15 | 0.475 ± 0.04 | 0.08 |
| 3 | 30 | 20.15 ± 5.51 | 0.27 | 69 ± 140.88 | 0.18 | 0.38 ± 0.03 | 0.09 |
There was a high degree of inter-sample variability in the area (CV = 41%), outline perimeter (CV = 61%), and wrinkledness of fibrosis (CV = 38%). The inter-sample variability in Hurst’s exponent was less (CV = 13%).
We have described a purely quantitative method of assessing liver fibrosis based on the theory of measure, which is the point of departure of all our concrete knowledge of the physical world, and the main reference for the construction of predictive and monitoring models[40].
During this study, our first difficulty was to measure the collagen islets making up liver fibrosis using standard metrics, because their irregularity excluded them from Euclidean geometry, which was created to describe smooth objects. Collagen islets can therefore only be measured using the principles of fractal mathematics and geometry[7-11].
Unlike the regular objects of Euclidean geometry, fractal objects do not have a single measure because it changes at every scale of observation as the result of the appearance of details that are imperceptible at lower magnifications, thus measurements have to be made at a well-defined scale[41].
The second difficulty was to identify the epistemological difference between the meanings of quantitative metric measures and the definition of a diagnosis of fibrosis in chronic inflammation or its progression to cirrhosis, which could be considered a radically different clinical condition.
After making numerous experiments with our computer program, to analyze entire Sirius red-stained biopsy sections we established that the most favorable magnification was 200 ×, thus this magnification was used to digitize the microscope images.
After this methodological study, which considered the process of fibrogenesis as nothing rather than a physical phenomenon, we asked ourselves three basic questions, namely what have we learned about the meaning of liver tissue fibrosis what new knowledge have we acquired after having measured the new canons of liver tissue architecture and classified their changes with scalars and how much can these new notions be used in clinical practice to discriminate the progression or regression of fibrosis
The first new notion was to extend the concept of the fractal dimension to metric measurements that might closely approximate the real magnitude of the irregular objects under observation.
Sensu stricto, the results of the intra-sample behavior and inter-sample variability study showed the non-representativeness of the perimeter and areas of fibrosis: the former due to its dependence on the extension of the bioptic specimen, and the latter for the high variability of the distribution of the inflammation process in the organ.
We added the staging of the evolution of ECM deposition towards stages of non-tolerability using the scalars obtained from the two-dimensional measurements of the area of the fibrotic mass. Although hardly representative and no more than a resonance of the mesomorphic process taking place in the environment, this information has some clinical interest if only as a very generic quantitative portrait of the general condition of the liver.
The quantitative relationships between the edge-interior of the fibrosis mass generated the new concept of its wrinkledness.
The collagen islets were categorized into three classes on the basis of the magnitude of their areas, which provided clues to their state of instability that indicated the activity of the fibrogenetic process. High presence of islets belonging to these subclasses according to the fractal geometry, is a signal of collagen structure instability in transition towards more stable states.
The distribution of the quantitative values of the areas covered by fibrosis in each category of the four semi-quantitative methods of evaluation clearly and simply confirmed the unreliability of the semi-quantitative systems themselves. This inadequacy could also be seen even when the histological preparations were analyzed by expert hepato-pathologists whose experience encompasses a large number of observed cases.
Interest in the collagen/parenchyma ratio led us to recognize the canons (mathematical laws) governing the natural “harmonic state of liver tissue”, by which the order that characterizes its organized fibrous and parenchymal components (considered prime bodies) in such a way can provide a definition of the natural histological architecture of liver tissue. This can be defined in two dimensions on the basis of the extension of the metric spaces covered by fibrous tissue (no more than 3%) and the parenchyma (97%). It can be intuitively understood that altered proportions between these spaces disrupt the natural harmonic state by creating disorder in the natural lobular structure of the liver tissue. In this sense, the words “measure” and “architectural alteration” in Ishak’s classical semi-quantitative definition (1995) …"[Staging]… is a measure of fibrosis, and architectural alteration, i.e. structural progression of the disease…" really indicate a rigorous metric value, and the term architectural alteration of this definition acquires the consistency of a measurable, scientific variable of state.
In order to quantify the architectural alteration, we used Hurst’s exponent, and analysis of its variability gave the following promising results: the least variability in thirty sequential sections (intra-sample variability), the greatest representativeness in six samples of hepatic tissue obtained from different parts of the liver (it was not possible to speak of lobes because of the advanced structural alterations induced by cirrhosis). This last result is currently further investigated in our laboratories.
In conclusion, although a number of serum fibrosis markers have been discordantly proposed[1-5,42-46], the results of this study strongly underline the primary role of liver biopsy in the qualitative diagnosis of chronic liver disease and its usefulness in evaluating fibrosis in a metrically rigorous manner. The use of quantitative descriptors of irregularly-shaped fibrosis should shed new insights into the dynamics of viral and non-viral liver diseases. We are concentrating on the clinical use of Hurst’s exponent after antiviral drug treatment as it can quantitatively demonstrate a drug’s effect on fibrosis with a very low error.
S- Editor Wang J L- Editor Wang XL E- Editor Bi L
| 1. | Poynard T, Imbert-Bismut F, Munteanu M, Messous D, Myers RP, Thabut D, Ratziu V, Mercadier A, Benhamou Y, Hainque B. Overview of the diagnostic value of biochemical markers of liver fibrosis (FibroTest, HCV FibroSure) and necrosis (ActiTest) in patients with chronic hepatitis C. Comp Hepatol. 2004;3:8. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 250] [Cited by in RCA: 280] [Article Influence: 13.3] [Reference Citation Analysis (0)] |
| 2. | Rosenberg WM, Voelker M, Thiel R, Becka M, Burt A, Schuppan D, Hubscher S, Roskams T, Pinzani M, Arthur MJ. Serum markers detect the presence of liver fibrosis: a cohort study. Gastroenterology. 2004;127:1704-1713. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 756] [Cited by in RCA: 759] [Article Influence: 36.1] [Reference Citation Analysis (0)] |
| 3. | Patel K, Gordon SC, Jacobson I, Hézode C, Oh E, Smith KM, Pawlotsky JM, McHutchison JG. Evaluation of a panel of non-invasive serum markers to differentiate mild from moderate-to-advanced liver fibrosis in chronic hepatitis C patients. J Hepatol. 2004;41:935-942. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 242] [Cited by in RCA: 241] [Article Influence: 11.5] [Reference Citation Analysis (0)] |
| 4. | Imbert-Bismut F, Ratziu V, Pieroni L, Charlotte F, Benhamou Y, Poynard T. Biochemical markers of liver fibrosis in patients with hepatitis C virus infection: a prospective study. Lancet. 2001;357:1069-1075. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1066] [Cited by in RCA: 1037] [Article Influence: 43.2] [Reference Citation Analysis (0)] |
| 5. | Lu LG, Zeng MD, Wan MB, Li CZ, Mao YM, Li JQ, Qiu DK, Cao AP, Ye J, Cai X. Grading and staging of hepatic fibrosis, and its relationship with noninvasive diagnostic parameters. World J Gastroenterol. 2003;9:2574-2578. [PubMed] |
| 6. | Rose S. What is wrong with reductionist explanations of behaviour. Novartis Found Symp. 1998;213:176-86; discussion 186-92, 218-21. [PubMed] |
| 7. | Dioguardi N, Grizzi F, Bossi P, Roncalli M. Fractal and spectral dimension analysis of liver fibrosis in needle biopsy specimens. Anal Quant Cytol Histol. 1999;21:262-266. [PubMed] |
| 8. | Grizzi F, Dioguardi N. A fractal scoring system for quantifying active collagen synthesis during chronic liver disease. Int J Chaos Theo Appl. 1999;2-3:39-44. |
| 9. | Dioguardi N, Grizzi F. Fractal dimension exponent for quantitative evaluation of liver collagen in bioptic specimens. In "Mathematics and Biosciences in interaction", Basel, Boston, Berlin: Birkhauser Press 2001; 113-120. |
| 10. | Dioguardi N, Franceschini B, Aletti G, Russo C, Grizzi F. Fractal dimension rectified meter for quantification of liver fibrosis and other irregular microscopic objects. Anal Quant Cytol Histol. 2003;25:312-320. [PubMed] |
| 11. | Dioguardi N, Franceschini B, Russo C, Grizzi F. Computer-aided morphometry of liver inflammation in needle biopsies. World J Gastroenterol. 2005;11:6995-7000. [PubMed] |
| 12. | Kleiner DE. The liver biopsy in chronic hepatitis C: a view from the other side of the microscope. Semin Liver Dis. 2005;25:52-64. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 50] [Cited by in RCA: 45] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 13. | Desmet VJ. Liver tissue examination. J Hepatol. 2003;39 Suppl 1:S43-S49. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 25] [Cited by in RCA: 19] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 14. | Bravo AA, Sheth SG, Chopra S. Liver biopsy. N Engl J Med. 2001;344:495-500. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1843] [Cited by in RCA: 1736] [Article Influence: 72.3] [Reference Citation Analysis (0)] |
| 15. | Brunt EM. Liver biopsy interpretation for the gastroenterologist. Curr Gastroenterol Rep. 2000;2:27-32. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 20] [Cited by in RCA: 19] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 16. | Brunt EM. Grading and staging the histopathological lesions of chronic hepatitis: the Knodell histology activity index and beyond. Hepatology. 2000;31:241-246. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 324] [Cited by in RCA: 339] [Article Influence: 13.6] [Reference Citation Analysis (0)] |
| 17. | Desmet V, Fevery J. Liver biopsy. Baillieres Clin Gastroenterol. 1995;9:811-828. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 10] [Cited by in RCA: 9] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 18. | Knodell RG, Ishak KG, Black WC, Chen TS, Craig R, Kaplowitz N, Kiernan TW, Wollman J. Formulation and application of a numerical scoring system for assessing histological activity in asymptomatic chronic active hepatitis. Hepatology. 1981;1:431-435. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2558] [Cited by in RCA: 2507] [Article Influence: 57.0] [Reference Citation Analysis (0)] |
| 19. | Scheuer PJ. Classification of chronic viral hepatitis: a need for reassessment. J Hepatol. 1991;13:372-374. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1130] [Cited by in RCA: 1198] [Article Influence: 35.2] [Reference Citation Analysis (0)] |
| 20. | Ishak K, Baptista A, Bianchi L, Callea F, De Groote J, Gudat F, Denk H, Desmet V, Korb G, MacSween RN. Histological grading and staging of chronic hepatitis. J Hepatol. 1995;22:696-699. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 3521] [Cited by in RCA: 3783] [Article Influence: 126.1] [Reference Citation Analysis (1)] |
| 21. | Bedossa P, Poynard T. An algorithm for the grading of activity in chronic hepatitis C. The METAVIR Cooperative Study Group. Hepatology. 1996;24:289-293. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2860] [Cited by in RCA: 3082] [Article Influence: 106.3] [Reference Citation Analysis (0)] |
| 22. | Kage M, Shimamatu K, Nakashima E, Kojiro M, Inoue O, Yano M. Long-term evolution of fibrosis from chronic hepatitis to cirrhosis in patients with hepatitis C: morphometric analysis of repeated biopsies. Hepatology. 1997;25:1028-1031. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 86] [Cited by in RCA: 82] [Article Influence: 2.9] [Reference Citation Analysis (0)] |
| 23. | Masseroli M, Caballero T, O'Valle F, Del Moral RM, Pérez-Milena A, Del Moral RG. Automatic quantification of liver fibrosis: design and validation of a new image analysis method: comparison with semi-quantitative indexes of fibrosis. J Hepatol. 2000;32:453-464. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 99] [Cited by in RCA: 93] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 24. | Pilette C, Rousselet MC, Bedossa P, Chappard D, Oberti F, Rifflet H, Maïga MY, Gallois Y, Calès P. Histopathological evaluation of liver fibrosis: quantitative image analysis vs semi-quantitative scores. Comparison with serum markers. J Hepatol. 1998;28:439-446. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 154] [Cited by in RCA: 147] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 25. | Wright M, Thursz M, Pullen R, Thomas H, Goldin R. Quantitative versus morphological assessment of liver fibrosis: semi-quantitative scores are more robust than digital image fibrosis area estimation. Liver Int. 2003;23:28-34. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 37] [Cited by in RCA: 30] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 26. | O'Brien MJ, Keating NM, Elderiny S, Cerda S, Keaveny AP, Afdhal NH, Nunes DP. An assessment of digital image analysis to measure fibrosis in liver biopsy specimens of patients with chronic hepatitis C. Am J Clin Pathol. 2000;114:712-718. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 88] [Cited by in RCA: 83] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 28. | Perrin J. La discontinuité de la matière. Revue du Mois. 1906;1:323-344. |
| 29. | Hausdorff F. Dimension and ausseres. Mathematishe Annalen. 1919;LXXIX; 157-179. |
| 30. | Richardson L. The problem of contiguity: an appendix of statistics of deadly quarrels. General Systems Yearbook. 1961;6:139-187. |
| 31. | Rigaut JP. Schoëvaërt-Brossault D, Downs AM, Landini G. Asymptotic fractals in the context of grey-scale images. J Microsc. 1998;189:57-63. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 22] [Cited by in RCA: 20] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 32. | Ruebner BH. Collagen formation and cirrhosis. Semin Liver Dis. 1986;6:212-220. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 12] [Cited by in RCA: 13] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 33. | Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal physiology. New York: Oxford University Press 1994; . |
| 34. | Hastings HM, Sugihara G. Fractals. A User's Guide for the Natural Sciences. Oxford: Oxford Science Publications 1993; . |
| 35. | Junqueira LC, Bignolas G, Brentani RR. Picrosirius staining plus polarization microscopy, a specific method for collagen detection in tissue sections. Histochem J. 1979;11:447-455. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1745] [Cited by in RCA: 1851] [Article Influence: 40.2] [Reference Citation Analysis (0)] |
| 36. | Hurst HE. Long-term storage capacity of reservoirs. Trans Amer Soc Civ Eng. 1951;116:770-808. |
| 37. | Hurst HE, Black RP, Simaiki YM. Long-term storage: an experimental study. London: Constable 1965; . |
| 38. | Bassingthwaighte JB, Raymond GM. Evaluation of the dispersional analysis method for fractal time series. Ann Biomed Eng. 1995;23:491-505. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 108] [Cited by in RCA: 68] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 39. | Rousselet MC, Michalak S, Dupré F, Croué A, Bedossa P, Saint-André JP, Calès P. Sources of variability in histological scoring of chronic viral hepatitis. Hepatology. 2005;41:257-264. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 409] [Cited by in RCA: 411] [Article Influence: 20.6] [Reference Citation Analysis (0)] |
| 40. | Rosen R. Fundamentals of measurements and representation of natural systems. Amsterdam: North-Holland 1978; . |
| 41. | Nonnenmacher TF, Baumann G, Barth A, Losa GA. Digital image analysis of self-similar cell profiles. Int J Biomed Comput. 1994;37:131-138. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 29] [Cited by in RCA: 21] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 42. | Lu LG, Zeng MD, Mao YM, Li JQ, Qiu DK, Fang JY, Cao AP, Wan MB, Li CZ, Ye J. Relationship between clinical and pathologic findings in patients with chronic liver diseases. World J Gastroenterol. 2003;9:2796-2800. [PubMed] |
| 43. | Tao J, Peng HQ, Cai WM, Dong FQ, Weng HL, Liu RH. Influence factors of serum fibrosis markers in liver fibrosis. World J Gastroenterol. 2003;9:2497-2500. [PubMed] |
| 44. | Zheng M, Cai WM, Weng HL, Liu RH. ROC curves in evaluation of serum fibrosis indices for hepatic fibrosis. World J Gastroenterol. 2002;8:1073-1076. [PubMed] |
| 45. | Rosenthal-Allieri MA, Peritore ML, Tran A, Halfon P, Benzaken S, Bernard A. Analytical variability of the Fibrotest proteins. Clin Biochem. 2005;38:473-478. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 31] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 46. | Rossi E, Adams L, Prins A, Bulsara M, de Boer B, Garas G, MacQuillan G, Speers D, Jeffrey G. Validation of the FibroTest biochemical markers score in assessing liver fibrosis in hepatitis C patients. Clin Chem. 2003;49:450-454. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 174] [Cited by in RCA: 171] [Article Influence: 7.8] [Reference Citation Analysis (0)] |