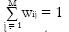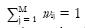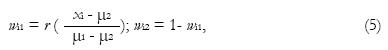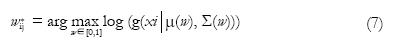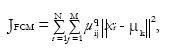Published online Nov 28, 2014. doi: 10.4329/wjr.v6.i11.855
Revised: September 3, 2014
Accepted: September 23, 2014
Published online: November 28, 2014
Processing time: 167 Days and 21.3 Hours
Quantitative analysis of magnetic resonance (MR) brain images are facilitated by the development of automated segmentation algorithms. A single image voxel may contain of several types of tissues due to the finite spatial resolution of the imaging device. This phenomenon, termed partial volume effect (PVE), complicates the segmentation process, and, due to the complexity of human brain anatomy, the PVE is an important factor for accurate brain structure quantification. Partial volume estimation refers to a generalized segmentation task where the amount of each tissue type within each voxel is solved. This review aims to provide a systematic, tutorial-like overview and categorization of methods for partial volume estimation in brain MRI. The review concentrates on the statistically based approaches for partial volume estimation and also explains differences to other, similar image segmentation approaches.
Core tip: Each voxel in a brain magnetic resonance imaging (MRI) may contain multiple types of tissue. Partial volume estimation refers to a generalized image segmentation task where the amount of each tissue type within each image voxel of brain MRI is solved. This is important for volume quantification and cortical thickness analysis due to the geometrical complexity of human brain structure. This review aims to provide a systematic, tutorial-like overview of methods for partial volume estimation in brain MRI.
- Citation: Tohka J. Partial volume effect modeling for segmentation and tissue classification of brain magnetic resonance images: A review. World J Radiol 2014; 6(11): 855-864
- URL: https://www.wjgnet.com/1949-8470/full/v6/i11/855.htm
- DOI: https://dx.doi.org/10.4329/wjr.v6.i11.855
Quantitative analysis of magnetic resonance (MR) brain images to gain knowledge about human brain structure is increasingly important. For example, various neuropsychiatric and neurodegenerative diseases, such as schizophrenia[1] and Alzheimer’s disease[2], alter the brain structure. By analyzing these alterations, a better understanding of the underlying disease mechanisms could be gained and diseases could potentially be diagnosed more rapidly and accurately[3]. This is important since brain diseases represent a major source of the overall disease burden[4] and are often associated with heavy impact to informal caregivers.
The typical quantitative analyses to detect and quantify differences in brain structure between two or more subject groups include voxel based morphometry[5] and cortical thickness analysis[6]. These analyses are facilitated by the development of automated MR image (MRI) segmentation algorithms, which are standard tools in modern neuroscience. The image processing chain leading to MRI segmentation and, finally, to statistical analyses, comprises of a long pipeline of different operations including skull stripping, intensity non-uniformity correction, tissue classification, registration to the stereotactic space and cortical surfaces extraction. The point of interest in this review is the tissue classification. This refers to assigning a tissue type label to each voxel of a brain image. Typically, the three main tissue types, white matter (WM), gray matter (GM), and cerebro-spinal fluid (CSF), are considered.
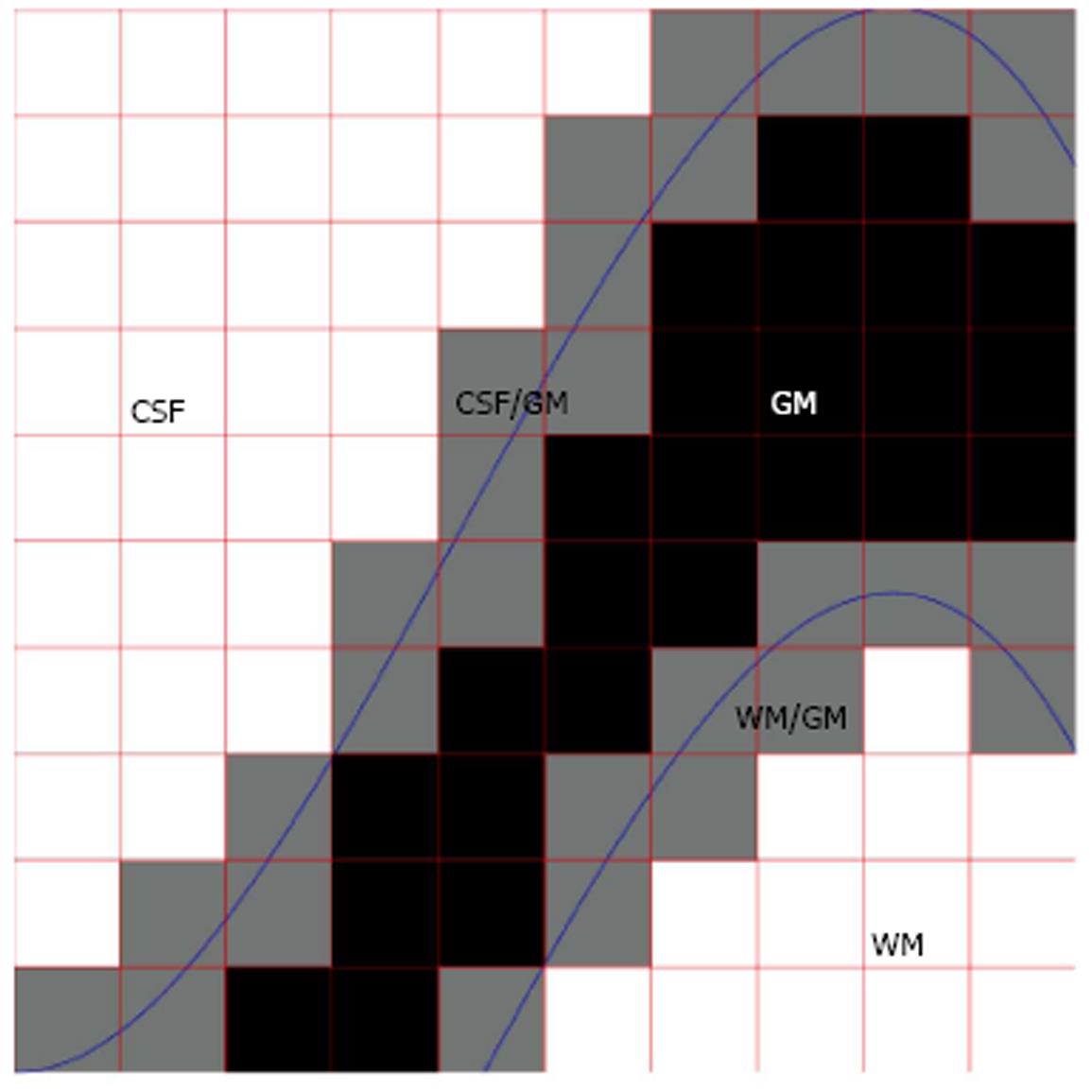
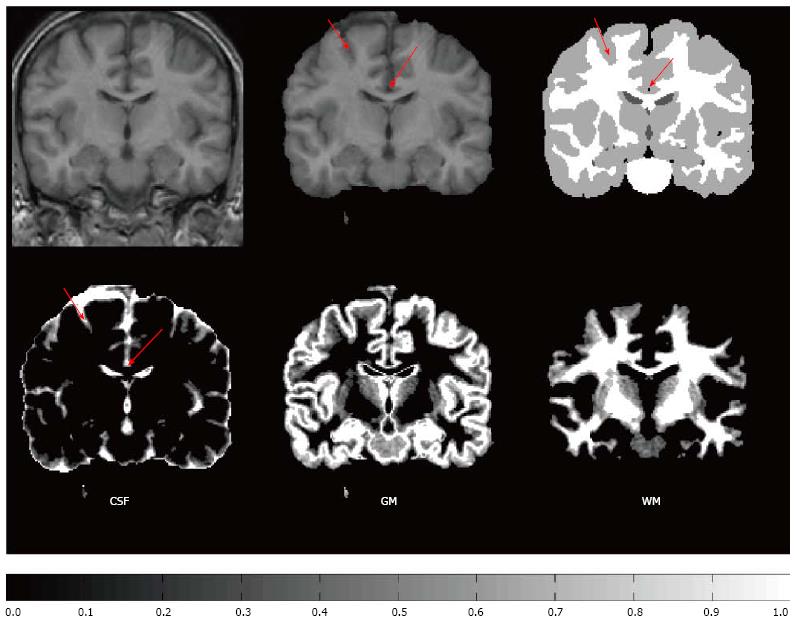
A single voxel may contain of several types of tissues due to the finite spatial resolution of the imaging device. This phenomenon, termed partial volume effect (PVE), complicates the segmentation process, and, due to the complexity of human brain anatomy, the PVE is an important factor when accurate brain structure quantification is needed; Figure 1 for a schematic explanation of the PVE in the context of brain MRI. González Ballester et al[7,8] reported that ignoring the PVE can lead to volume measurement errors in the range of 20%-60%. Most widely used MRI segmentation algorithms account for PVE, for example by incorporating extra tissue classes[9-11]. Ruan et al[12] demonstrated that the intensity distributions of the partial volume voxels can be approximated using Gaussian distributions and an early work attributed the non-normality of the intensity distributions of the tissue classes to partial volume artefact[13]. However, some algorithms take a step further and try to solve an extended version of the tissue classification problem, where the amount of each tissue type within each voxel is solved. For example, hard or crisp tissue classification provides information whether a particular voxel is WM, GM, or CSF. In the extended problem, one wants to know that a voxel contains 20% GM, 80% WM and 0% of CSF and we say that the partial volume coefficients (PVCs) are 20% for GM, 80% for WM and 0% for CSF. The extended problem has various names. It has been referred to as fuzzy segmentation, partial volume segmentation, partial volume estimation, and tissue fraction estimation. It will be referred to as partial volume estimation in the remainder of this paper. In order for the partial volume estimation problem to be solvable, the intensity of a partial volume voxel has to be expressed with a model that depends on the parameters of image intensity distributions of pure tissue classes. Figure 2 exemplifies partial volume estimation as compared to hard tissue classification and also points out a specific problem of hard tissue classification particularly important to cortical thickness computations. Namely, insufficient image resolution may lead to hard tissue classification miss sulcal CSF and this may subsequently lead to incorrect cortical thickness computation if hard tissue classification is used as a preprocessing operation to the cortical thickness computation.
This review aims to provide a systematic, tutorial-like overview and categorization for different approaches for partial volume estimation in brain MRI. In addition of the author’s knowledge about existing literature, the articles to be included in this review were searched on Pubmed: Search term: [(magnetic resonance [Title/Abstract] OR MRI [Title/Abstract]) AND brain [Title/Abstract] AND partial volume [Title/Abstract] AND (segmentation [Title/Abstract] OR tissue classification [Title/Abstract] OR partial volume coefficient estimation [Title/Abstract])] NOT (PET [Title/Abstract] OR emission tomography [Title/Abstract]). The search yielded 80 articles, majority of which were found relevant to this review.
The algorithms introduced in next sections require various image pre-processing steps to be performed before the partial volume estimation can take place. The pre-processing pipeline can include intensity non-uniformity correction, brain extraction (or skull stripping) and registration to a sterotactic space.
Intensity non-uniformity correction is required because MR images are known to contain low frequency spatial intensity variations often referred to as radio frequency inhomogeneity or shading artifact[14]. All segmentation algorithms in brain MRI must account for this artifact to produce accurate segmentations. There are several ways to correct for the shading artifact[14]. This can be assumed to be an image pre-processing step or to be performed jointly with the PV estimation, interleaving PV estimation (segmentation) and non-uniformity correction steps. In what follows, we will assume that the images have been corrected for this artifact.
Although we are interested in segmentation of the brain tissues, brain MR images contain signal from other, extracerebral tissue types, such as skull or scalp. Because these extracerebral tissue types are often irrelevant for brain image quantification, it is useful to mask out the voxels outside the brain out before the PV estimation. This is termed skull stripping or brain extraction and the reference[15] provides a comparison of skull stripping algorithms.
The registration to stereotactic space is usually carried out to be able to utilize information of the tissue type probability maps, which, for each voxel, give a prior probability that the voxel is of certain issue type[16]. It should be noted that this is not as useful for partial volume estimation as it can be for hard segmentation, because tissue probability maps provide no information on tissue fractions[17]. Moreover, if the registered images are resampled to the stereotactic space, this amplifies the partial volume effect and may not be a recommended action.
The most commonly used model of PVE in brain MRI is the mixel model[18]. The mixel model assumes that each intensity value in the image is a realization of a weighted sum of random variables (RVs), each of which characterizes a pure tissue type. The original formulation[18] requires images to be multispectral, i.e., that image data from multiple pulse sequences are available (for example, T1, T2,and proton density weighted images). However, there are approaches to overcome this problem by utilizing clever approximations as we shall see in Section 3.2.
We now proceed to a more formal description of the mixel model. For this, we need to establish some notation. The observed image is X = {xi: i = 1,…,N}, with the voxel intensity xi∈ RK, and K the number of data channels in the multispectral case. For example, if we have T1-, T2-, and proton density-weighted images, then K = 3. N denotes the number of brain voxels in the image and i is the voxel index. The voxel index has three components that correspond to the position of the voxel in the left-right, anterior-posterior, and inferior-superior axes. There are M tissue types in the image. Typically, M is equal to 3, and the tissue types are WM, GM, and CSF. The mixel model is statistically based. Thus, a voxel intensity xi is considered to be a realization of random variable xi. (We use bold-face symbols to refer to random variables and the corresponding normal-face symbols denote their realizations.) Similarly, each tissue type j is described by a random variable lj , which is assumed to be distributed according to the multivariate normal distribution with the mean μj and covariance Σj. Random variable xi is written as a weighted sum
Math 1
where n represents measurement noise, typically assumed to be Gaussian (with a covariance matrix Σ*) and partial volume coefficients (PVCs) wij∈ [0, 1] for all i,j and
Math 2
for all i. The PVCs model the fraction of each tissue type in the voxel, for example, if wiGM has a value of 0.8 then the voxel contains 80% of the GM tissue type. This is similar to the fuzzy classification/segmentation problem, but in the mixel model the coefficients wij specifically model the fraction of tissue type j present in the voxel i. We will return to connections of the mixel model and the Fuzzy C-means algorithm in Section 5.
In practice, the mixel model has to be simplified because it is impossible to distinguish between measurement noise and variability within tissue types. Various simplifications have been studied by Santago et al[19,20]. They identified two possible types of simplification, namely, the sampling noise model and material dependent noise model as depicted in Figure 3. The sampling noise model assumes that all the randomness in the model is due to measurement noise. This leads to a model, where the tissue types are described by mean intensities of tissue types:
Math 3
The material dependent noise model is obtained by embedding the measurement noise into material noise components, i.e., n is dropped from Eq. (1)
Math 4
This model is more complex than the sampling noise model, but it is probably more realistic.
Direct solutionviapenalized least squares: Assuming the sampling noise model, the PVCs can be solved directly from Eq. (2) if enough data channels are available[18]. Denoting a matrix of all PVCs by w, the least squares criterion to minimize for solving Eq. (2) is written as
Math 5
with constraints that
Math 6
and 0 ≤wij≤ 1. Note that this equation can be solved individually for each voxel. In the case of single image channel and two tissue types, the solution is particularly simple:
Math 7
and the function r limits the solution to the interval from 0 to 1, i.e., r (y) = 0 when y < 0, r(y) = y when 0 ≤y≤ 1, and r (y) = 1 when y > 1. This solution is also the maximum likelihood solution and it accounts to a simple scaling of the image intensities to the interval from 0 to 1. For this reason, the solution is also very noisy and Choi et al[18] suggested to regularize it with a Markov Random Field (MRF) prior (see also Li et al[21]). The idea is that PVCs of neighboring voxels should have similar values. This leads to a modified criterion to minimize, with the same constraints as above,
Math 8
where the term P(w) penalizes differences between wi = [wi1,…,wiM] and wk = [wk1,…,wkM] if the voxels i and k are neighbours. Unfortunately, this objective cannot be anymore minimized separately for each voxel, but all the voxels must be taken into account. Besag et al[22] used Iterative Conditional Modes algorithm to minimize the penalized least squares criterion in Eq.(6).
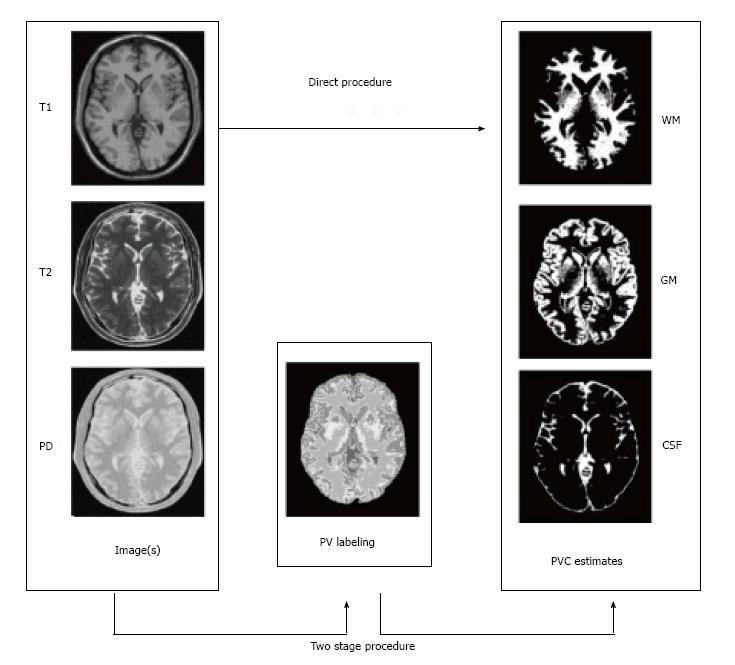
Two step algorithms: The simple two-class, one-channel solution above motivates a set of techniques allowing the standard PVC estimation for three tissue types even if just data from just a single image (usually T1-weighted) is available. The idea is that since the combination of more than two tissue types in a voxel is very rare, we can estimate which two tissue types are present in a voxel before the PVC estimation; Alike idea was already mentioned for multichannel data in[18,23]. The steps of the two step algorithm can be given as follows, and they are schematically represented in Figure 4: (1) Partial volume classification: Estimate which is most likely tissue type configuration containing at most two tissue types in each voxel; and (2) PVC estimation: Solve the partial volume estimation problem limited to tissue types found in Step 1 for all the voxels.
There are at least three different approaches to solve the task in the step 1. In the simplest approach, used for example in the reference[24], the tissue classes are ordered based on their mean values so that μ1< μ2< ..... < μM. Then, if the intensity value xi lies in the interval [μk,μk+1], it is assumed that the voxel i is a mixture of tissue types k and k + 1. This simple model does not account for the noise in the images and is not applicable for multichannel data because it assumes that the mean intensity values of tissue types can be ordered. The second approach is to detect most likely pure tissue types within the voxel based on the Bayes classifier[18,23]. This is done computing the two most probable tissue types within a voxel. However, this approach, as the first one, ignores the possibility that voxels may be composed of a single tissue type. The third and preferred approach, which is we term as probabilistic partial volume classification, fixes the just mentioned problem. The probabilistic partial volume classification approach is to compute the probability of each possible tissue type mixture appearing in the voxel[19,20,25-27]. For example, if the tissue types of interest are WM, GM, and CSF, the following 6 probabilities are computed: (1) Voxel is solely CSF; (2) Voxel is solely GM; (3) Voxel is solely WM; (4) voxel is a mixture of background and CSF; (5) voxel is a mixture of CSF and GM; and (6) voxel is a mixture of GM and WM. (Some tissue type combinations are not considered due to their rarity in the brain.) The technical problem in the probabilistic partial volume classification approach is the construction of the probability models for mixed tissue classes; the class conditional densities for pure tissue classes are modelled by the normal density. The probability densities for the mixed tissue types can be constructed based on a marginalization technique developed originally in references[19,20] and further applied in references[25-28]. The idea is to integrate out the variable wi1describing the percentage of tissue type 1 in a voxel by numerical integration. Note that with current computers the numerical integration does not present computational problem and can be solved very fast[28]. Advantages of this more complicated probabilistic approach over the two simple approaches include possibility to include spatial regularization in the form of MRFs to the step 1[25,26] and the applicability to multispectral images[26]. Additionally, it is often expected that the number of the pure tissue voxels should be greater than the number of mixed tissue voxels. The probabilistic partial volume classification includes automatic and elegant control for this issue that has been solved elsewhere by using Bayesian methods at the expense of introducing extra user-defined parameters[24,29].
Once the tissue types that are probable to appear in a voxel are determined, then the PVCs can be estimated using Eq. (5) if the sampling noise model is assumed. Note that if voxel i is determined to be a voxel of pure tissue type k, then wik = 1 and wij = 0 for other tissue types j ≠ k. One can also adopt the material dependent noise model leading to a maximum likelihood criterion. If i is a mixed voxel of tissue types j and k, the maximum-likelihood solution is
Math 9
where μ(w) = wμj + (1-w)μk; Σ(w) = w2Σj + (1-w)2Σk or Σ(w) = wΣj + (1-w)Σk. Furthermore, wik* = 1 - wij* and all the other PVCs are zero. The correct model for Σ(w) has caused some controversy (see the references[30,31] for details). The difference in the two models is that the first one (Σ(w) = w2Σj + (1 - w)2Σk) results in a more regularized solution of Eq. (7) while the second one (Σ(w) = wΣj + (1 - w)Σk ) is conceptually more pleasing. The maximum-likelihood PVC-estimate in Eq. (7) is solved by a simple grid search. Extensions to the maximum likelihood principle of Eq. (7) include Bayesian methods[24].
As mentioned above, the two-step algorithms can use the MRF prior to regularize the partial volume classification and this has been demonstrated to lead to more accurate partial volume estimates when the images are noisy[25]. The use of the MRF requires the user to set a proper weighting parameter for the prior which may be considered as a disadvantage[8]. However, often quoted disadvantage of the added computational cost (e.g., the reference[8]) of the MRF, can be overcome by new rapid algorithms capable of performing MRF based segmentation of the typical 3-D MR images within few seconds[28]. While the two-step algorithms often use spatial MRF prior during the partial volume classification step, they typically do not utilize spatial information during the second, PVC estimation, step. Manjón et al[27] introduced an MRF for modelling of the spatial information during the PVC estimation step and compared it to the usage of prefiltering the images with a non-local means filter. The results suggested that using spatial information improved the PVC estimates and non-local means filtering performed better than the MRF-based approach.
Discretization approaches: An alternative to try to find real-valued PVC estimates is to discretize the PVC estimation problem[32-34]. This means that instead of letting each PVC wij lie freely in the interval from zero to one, the discretization-based methods restrict the PVCs to have only a discrete set of values. For example, wij can be 0, 0.1, 0.2,…,1.0. The discretization-based methods then try to solve maximally probable PVCs from this discretized set resorting MRF approaches to model spatial interaction between adjacent voxels[32-34]. While the restriction to a discrete set of PVC values is perfectly reasonable given the noisiness of the images, the discretization approaches are usually very time consuming, especially when compared to fast two step approaches[25,28].
The necessary model parameters μj,j = 1,…,M and Σ* or Σj,j = 1,…,M must be estimated before or during the solution of the mixel model. Correct estimation of these parameters is essential for partial volume estimation[35]. Tohka et al[26] identified three potential approaches to the parameter estimation problem: (1) histogram analysis; (2) simultaneous parameter, and partial volume estimation by expectation maximization (EM)-like algorithms; and (3) the estimation based on a hard segmentation of the image.
The conceptually simplest alternative is to fit a parametric model (a mixture model of pure and mixed tissue intensity densities) to an image histogram. The objective function can be based on the maximum likelihood or least squares criterion. The disadvantage of parametric model fitting is that the formulated minimization problem is complex and non-convex rendering the standard optimization algorithms useless. Various global optimization algorithms, including genetic algorithms and tree annealing, have been used for the task[19,36]. The EM-like algorithms start from an initial rough parameter estimates and refine the estimates jointly with the partial volume estimation[32,34] or classification[37] through alternating expectation and maximization steps. This can guarantee accurate parameter estimates, but the estimates depend strongly on the initial guess and the convergence of the process can be slow. The third alternative is to generate an initial rough segmentation of the image, and thereafter use outlier detection techniques based on the mathematical morphology, robust point estimates, or image gradient values to prune the set of voxels belonging to a certain tissue class[25,26,35,38,39]. Comparisons of these three techniques have been reported in the references[26,35]. The main result of these comparisons has been that the parameter estimation based on the hard segmentation of the image is fast and usually, but not always, works as well or better than the other two approaches.
The standard Fuzzy C-means (FCM) algorithm optimizes a cost function
Math 10
where uij are the fuzzy membership values μk are the class centroids, and q is the fuzzification parameter. This objective function and its modifications have been widely and successfully used for brain MRI tissue classification[40-43]. As shown in the reference[29], if q = 3, M = 2, and K = 1, optimizing the objective JFCM for fixed centroids leads to the identical PVCs as PVCs derived based on Eq. (5). However, with more than two tissue types or multispectral data, fuzzy segmentations by FCM and mixel model are different.
Often the tissue classification is casted as the Bayesian decision problem[9,16,17,44,45]. In that, one tries to estimate the posterior probability map that the tissue type is c given the image intensities. Often approaches use prior information from tissue probability maps[9,16] or MRFs[44,45] or both[17]. It should be noted that the tissue type probabilities are different from the partial volume coefficients. The exact difference of the segmentation results depends on the probability model selected, but usually these Bayesian tissue classifiers produce more crisp tissue type maps than the partial volume estimation algorithms. This issue and its ramifications are considered in a more detail by Manjón et al[27].
Voxel-based morphometry (VBM) involves a voxel-wise comparison of the local concentration of gray matter between two groups of subjects. The procedure consists of segmenting the gray matter from the MR images and spatially normalizing these gray matter images from all the subjects in the study into the same stereotactic space[5]. These gray matter images can either represent GM tissue probabilities, for example, as in the reference[46] or GM tissue fractions resulting partial volume estimation, for example, as in the reference[47]. While it seems clear that the PVCs are better representations of gray matter density than gray matter probabilities, it is not clear whether this particular modelling choice has a major effect on the accuracy of the results. To author’s knowledge, gray matter probability and gray matter PV-coefficient based VBM methods have not been directly compared. Tardif et al[48] examined two pipelines resulting in GM probability based VBM and PVC based VBM but the main focus of the work was on a comparison of 1.5T and 3T imaging protocols. The VBM8 software package (http://dbm.neuro.uni-_jena.de/vbm/) offers possibility to VBM using PVCs[49].
Cortical thickness is a quantitative measure describing the combined thickness of the layers of the cerebral cortex that can be measured using MRI either using mesh based[6,50,51] or voxel based techniques[52]. The thickness of the cortex, and its local variations, are of great interest in both normal development as well as a wide variety of neurodegenerative and psychiatric disorders[6]. Cortex is a highly folded structure with an approximate average thickness of 2.5 mm[53] and hence it is not difficult to appreciate that the partial volume effect has been an important consideration when measuring cortical thickness. Both surface mesh based[54] and voxel based[55-57] cortical thickness measures can be shown to be improved if the partial volume effect is taken into account. Especially, as demonstrated in Figure 2 and discussed further in the references[26,54], hard tissue classifications may miss some of the sulcal CSF because of an insufficient image resolution. This causes incorrect reconstruction of the GM/CSF boundary, which, in turn, leads to errors in the cortical thickness computation.
Other applications of segmentation with the PVE modeling identified during the literature review were segmentation of the brain images of the neonates[58-61], hemisphere segmentation and related shape analysis[62,63], EEG source localization[64], and lesion load computations based on MRI[65-68]. Especially, in the case of the Multiple Sclerosis (MS) lesion volumetry, the correction for the partial volume effects has a large positive effect on the reproducibility and accuracy of the analysis[69]. In particular, it was found to be important in avoiding of misclassification of some non-lesion voxels (between CSF and brain tissue) into lesion voxels[69].
An interesting recent development in MRI segmentation and partial volume estimation is the use of quantitative tissue type maps for the purpose[70-72]. For example, Ahlgren et al[70] utilized the signal of a spoiled gradient-recalled echo (SPGR) sequence acquired with multiple flip angles to map T1, and subsequently to fit of a multi-compartment model yielding parametric maps of partial volume estimates of the different compartments. West et al[71] used quantitative MRI values of the longitudinal relaxation rate, the transverse relaxation rate and the proton density to define tissues (WM,GM,CSF) and constructed a lookup table for partial volume estimation. These quantitative approaches show good potential to improve the partial volume estimation accuracy. Another recent development is the use of high-field MRI to map smaller and smaller brain structures[73], such cortical layers or hippocampal subfields[74]. These efforts will benefit from automated segmentation. Despite of improved image resolution provided by higher field strengths the problems related to partial volume effect will remain as the structures of interest will become smaller at the same time. For example, while the improved image resolution will diminish (but not completely erase) the challenges related to partial volume effect in the cortical thickness computation, it will also possibly allow studies concerning individual cortical layers requiring a higher image resolution, where partial volume effect is again an important consideration.
P- Reviewer: Logeswaran R, Sheehan JR, Walter M S- Editor: Ji FF L- Editor: A E- Editor: Lu YJ
| 1. | Shenton ME, Dickey CC, Frumin M, McCarley RW. A review of MRI findings in schizophrenia. Schizophr Res. 2001;49:1-52. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1677] [Cited by in RCA: 1610] [Article Influence: 67.1] [Reference Citation Analysis (0)] |
| 2. | Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Liu E. The Alzheimer’s Disease Neuroimaging Initiative: a review of papers published since its inception. Alzheimers Dement. 2013;9:e111-e194. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 307] [Cited by in RCA: 342] [Article Influence: 28.5] [Reference Citation Analysis (0)] |
| 3. | Frisoni GB, Fox NC, Jack CR, Scheltens P, Thompson PM. The clinical use of structural MRI in Alzheimer disease. Nat Rev Neurol. 2010;6:67-77. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 1557] [Cited by in RCA: 1248] [Article Influence: 83.2] [Reference Citation Analysis (0)] |
| 4. | Olesen J, Leonardi M. The burden of brain diseases in Europe. Eur J Neurol. 2003;10:471-477. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 161] [Cited by in RCA: 143] [Article Influence: 6.5] [Reference Citation Analysis (0)] |
| 5. | Ashburner J, Friston KJ. Voxel-based morphometry--the methods. Neuroimage. 2000;11:805-821. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 6199] [Cited by in RCA: 6204] [Article Influence: 248.2] [Reference Citation Analysis (0)] |
| 6. | Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA. 2000;97:11050-11055. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 4495] [Cited by in RCA: 4533] [Article Influence: 181.3] [Reference Citation Analysis (0)] |
| 7. | González Ballester MA, Zisserman A, Brady M. Segmentation and measurement of brain structures in MRI including confidence bounds. Med Image Anal. 2000;4:189-200. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 31] [Cited by in RCA: 24] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 8. | González Ballester MA, Zisserman AP, Brady M. Estimation of the partial volume effect in MRI. Med Image Anal. 2002;6:389-405. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 109] [Cited by in RCA: 111] [Article Influence: 4.8] [Reference Citation Analysis (0)] |
| 9. | Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839-851. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 5524] [Cited by in RCA: 6152] [Article Influence: 307.6] [Reference Citation Analysis (0)] |
| 10. | Reddick WE, Glass JO, Cook EN, Elkin TD, Deaton RJ. Automated segmentation and classification of multispectral magnetic resonance images of brain using artificial neural networks. IEEE Trans Med Imaging. 1997;16:911-918. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 217] [Cited by in RCA: 95] [Article Influence: 5.3] [Reference Citation Analysis (0)] |
| 11. | Cuadra MB, Cammoun L, Butz T, Cuisenaire O, Thiran JP. Comparison and validation of tissue modelization and statistical classification methods in T1-weighted MR brain images. IEEE Trans Med Imaging. 2005;24:1548-1565. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 290] [Cited by in RCA: 289] [Article Influence: 14.5] [Reference Citation Analysis (0)] |
| 12. | Ruan S, Jaggi C, Xue J, Fadili J, Bloyet D. Brain tissue classification of magnetic resonance images using partial volume modeling. IEEE Trans Med Imaging. 2000;19:1179-1187. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 104] [Cited by in RCA: 63] [Article Influence: 2.5] [Reference Citation Analysis (0)] |
| 13. | Bullmore E, Brammer M, Rouleau G, Everitt B, Simmons A, Sharma T, Frangou S, Murray R, Dunn G. Computerized brain tissue classification of magnetic resonance images: a new approach to the problem of partial volume artifact. Neuroimage. 1995;2:133-147. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 35] [Cited by in RCA: 27] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 14. | Vovk U, Pernus F, Likar B. A review of methods for correction of intensity inhomogeneity in MRI. IEEE Trans Med Imaging. 2007;26:405-421. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 636] [Cited by in RCA: 370] [Article Influence: 20.6] [Reference Citation Analysis (0)] |
| 15. | Shattuck DW, Prasad G, Mirza M, Narr KL, Toga AW. Online resource for validation of brain segmentation methods. Neuroimage. 2009;45:431-439. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 126] [Cited by in RCA: 88] [Article Influence: 5.5] [Reference Citation Analysis (0)] |
| 16. | Ashburner J, Friston K. Multimodal image coregistration and partitioning--a unified framework. Neuroimage. 1997;6:209-217. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 685] [Cited by in RCA: 664] [Article Influence: 23.7] [Reference Citation Analysis (0)] |
| 17. | Tohka J, Dinov ID, Shattuck DW, Toga AW. Brain MRI tissue classification based on local Markov random fields. Magn Reson Imaging. 2010;28:557-573. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 50] [Cited by in RCA: 33] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 18. | Choi HS, Haynor DR, Kim Y. Partial volume tissue classification of multichannel magnetic resonance images-a mixel model. IEEE Trans Med Imaging. 1991;10:395-407. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 206] [Cited by in RCA: 121] [Article Influence: 3.6] [Reference Citation Analysis (0)] |
| 19. | Santago P, Gage HD. Quantification of MR brain images by mixture density and partial volume modeling. IEEE Trans Med Imaging. 1993;12:566-574. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 105] [Cited by in RCA: 57] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 20. | Santago P, Gage HD. Statistical models of partial volume effect. IEEE Trans Image Process. 1995;4:1531-1540. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 70] [Cited by in RCA: 46] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 21. | Li X, Li L, Lu H, Liang Z. Partial volume segmentation of brain magnetic resonance images based on maximum a posteriori probability. Med Phys. 2005;32:2337-2345. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 46] [Cited by in RCA: 45] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 22. | Besag J. On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society, Series B. 1986;48:259-302 Available from: http: //www.jstor.org/stable/2345426. |
| 23. | Choi H, Haynor D, Kim Y. Multivariate tissue classification of mri images for 3-d volume reconstruction-a statistical approach. SPIE vol. 1092, Medical Imaging III: Image Processing 1989; 183-193. |
| 24. | Brouwer RM, Hulshoff Pol HE, Schnack HG. Segmentation of MRI brain scans using non-uniform partial volume densities. Neuroimage. 2010;49:467-477. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 40] [Cited by in RCA: 36] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 25. | Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using a partial volume model. Neuroimage. 2001;13:856-876. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 733] [Cited by in RCA: 539] [Article Influence: 22.5] [Reference Citation Analysis (0)] |
| 26. | Tohka J, Zijdenbos A, Evans A. Fast and robust parameter estimation for statistical partial volume models in brain MRI. Neuroimage. 2004;23:84-97. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 503] [Cited by in RCA: 526] [Article Influence: 25.0] [Reference Citation Analysis (0)] |
| 27. | Manjón JV, Tohka J, Robles M. Improved estimates of partial volume coefficients from noisy brain MRI using spatial context. Neuroimage. 2010;53:480-490. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 40] [Cited by in RCA: 41] [Article Influence: 2.7] [Reference Citation Analysis (0)] |
| 28. | Tohka J. FAST-PVE: Extremely fast markov random field based brain MRI tissue classification. 7944. SCIA: Springer 2013; 266-276. [RCA] [DOI] [Full Text] [Cited by in Crossref: 4] [Cited by in RCA: 4] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 29. | Pham DL, Prince J. Partial volume estimation and the fuzzy c-means algorithm. ICIP 98. Proceedings. 1998;819-822. [DOI] [Full Text] |
| 30. | Bromiley P, Thacker N. Multi-dimensional medical image segmentation with partial volume and gradient modelling. Annals of the BMVA. 2008;1-22 Available from: http: //www.bmva.org/annals/2008/2008-0002.pdf. |
| 31. | Bromiley P, Thacker N. Multi-dimensional medical image segmentation with partial volume and gradient modelling. Mathematical derivations and proofs. Annals of the BMVA. 2008;1-11 Available from: http: //www.bmva.org/annals/2008/2008-0002-supplement.pdf. |
| 32. | Bricq S, Collet Ch, Armspach JP. Unifying framework for multimodal brain MRI segmentation based on Hidden Markov Chains. Med Image Anal. 2008;12:639-652. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 59] [Cited by in RCA: 32] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 33. | Ruan S, Moretti B, Fadili J, Bloyet D. Fuzzy markovian segmentation in application of magnetic resonance images. Comput Vis Image Und. 2002;85:54-69. [DOI] [Full Text] |
| 34. | Van Leemput K, Maes F, Vandermeulen D, Suetens P. A unifying framework for partial volume segmentation of brain MR images. IEEE Trans Med Imaging. 2003;22:105-119. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 207] [Cited by in RCA: 126] [Article Influence: 5.7] [Reference Citation Analysis (0)] |
| 35. | Manjón JV, Tohka J, García-Martí G, Carbonell-Caballero J, Lull JJ, Martí-Bonmatí L, Robles M. Robust MRI brain tissue parameter estimation by multistage outlier rejection. Magn Reson Med. 2008;59:866-873. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 51] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 36. | Tohka J, Krestyannikov E, Dinov ID, Graham AM, Shattuck DW, Ruotsalainen U, Toga AW. Genetic algorithms for finite mixture model based voxel classification in neuroimaging. IEEE Trans Med Imaging. 2007;26:696-711. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 78] [Cited by in RCA: 48] [Article Influence: 2.7] [Reference Citation Analysis (0)] |
| 37. | Noe A, Gee J. Partial volume segmentation of cerebral MRI scans with mixture model clustering. of Information Processing in Medical Imaging. IPMI: 17th International Conference 2001; 423-430. [RCA] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 13] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 38. | Wang D, Doddrell DM. A segmentation-based and partial-volume-compensated method for an accurate measurement of lateral ventricular volumes on T(1)-weighted magnetic resonance images. Magn Reson Imaging. 2001;19:267-273. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 18] [Cited by in RCA: 18] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 39. | Wang D, Doddrell DM. MR image-based measurement of rates of change in volumes of brain structures. Part I: method and validation. Magn Reson Imaging. 2002;20:27-40. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 15] [Cited by in RCA: 16] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 40. | Suckling J, Sigmundsson T, Greenwood K, Bullmore ET. A modified fuzzy clustering algorithm for operator independent brain tissue classification of dual echo MR images. Magn Reson Imaging. 1999;17:1065-1076. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 122] [Cited by in RCA: 97] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 41. | Ortiz A, Palacio AA, Górriz JM, Ramírez J, Salas-González D. Segmentation of brain MRI using SOM-FCM-based method and 3D statistical descriptors. Comput Math Methods Med. 2013;2013:638563. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 41] [Cited by in RCA: 43] [Article Influence: 3.6] [Reference Citation Analysis (0)] |
| 42. | Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans Med Imaging. 1999;18:737-752. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 602] [Cited by in RCA: 347] [Article Influence: 13.3] [Reference Citation Analysis (0)] |
| 43. | Yoon UC, Kim JS, Kim JS, Kim IY, Kim SI. Adaptable fuzzy C-Means for improved classification as a preprocessing procedure of brain parcellation. J Digit Imaging. 2001;14:238-240. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 13] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 44. | Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE Trans Med Imaging. 1999;18:897-908. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 753] [Cited by in RCA: 558] [Article Influence: 21.5] [Reference Citation Analysis (0)] |
| 45. | Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20:45-57. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 4952] [Cited by in RCA: 4500] [Article Influence: 187.5] [Reference Citation Analysis (0)] |
| 46. | Good CD, Johnsrude I, Ashburner J, Henson RN, Friston KJ, Frackowiak RS. Cerebral asymmetry and the effects of sex and handedness on brain structure: a voxel-based morphometric analysis of 465 normal adult human brains. Neuroimage. 2001;14:685-700. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 894] [Cited by in RCA: 880] [Article Influence: 36.7] [Reference Citation Analysis (0)] |
| 47. | Nagano-Saito A, Washimi Y, Arahata Y, Kachi T, Lerch JP, Evans AC, Dagher A, Ito K. Cerebral atrophy and its relation to cognitive impairment in Parkinson disease. Neurology. 2005;64:224-229. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 211] [Cited by in RCA: 225] [Article Influence: 11.3] [Reference Citation Analysis (0)] |
| 48. | Tardif CL, Collins DL, Pike GB. Regional impact of field strength on voxel-based morphometry results. Hum Brain Mapp. 2010;31:943-957. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 29] [Cited by in RCA: 37] [Article Influence: 2.5] [Reference Citation Analysis (0)] |
| 49. | Gaser C. Partial volume segmentation with adaptive maximum a posteriori (MAP) approach. NeuroImage. 2009;47: S121. [RCA] [DOI] [Full Text] [Cited by in Crossref: 27] [Cited by in RCA: 36] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 50. | MacDonald D, Kabani N, Avis D, Evans AC. Automated 3-D extraction of inner and outer surfaces of cerebral cortex from MRI. Neuroimage. 2000;12:340-356. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 626] [Cited by in RCA: 586] [Article Influence: 23.4] [Reference Citation Analysis (0)] |
| 51. | Lerch JP, Evans AC. Cortical thickness analysis examined through power analysis and a population simulation. Neuroimage. 2005;24:163-173. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 530] [Cited by in RCA: 570] [Article Influence: 28.5] [Reference Citation Analysis (0)] |
| 52. | Hutton C, De Vita E, Ashburner J, Deichmann R, Turner R. Voxel-based cortical thickness measurements in MRI. Neuroimage. 2008;40:1701-1710. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 151] [Cited by in RCA: 162] [Article Influence: 9.5] [Reference Citation Analysis (0)] |
| 53. | Zilles K. Architecture of the Human Cerebral Cortex. In Paxinos G, Mai JK, The human nervous system. 2nd ed. San Diego: Elsevier 2004; 997-1060. |
| 54. | Kim JS, Singh V, Lee JK, Lerch J, Ad-Dab’bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC. Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. Neuroimage. 2005;27:210-221. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 651] [Cited by in RCA: 652] [Article Influence: 32.6] [Reference Citation Analysis (0)] |
| 55. | Rueda A, Acosta O, Couprie M, Bourgeat P, Fripp J, Dowson N, Romero E, Salvado O. Topology-corrected segmentation and local intensity estimates for improved partial volume classification of brain cortex in MRI. J Neurosci Methods. 2010;188:305-315. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 22] [Cited by in RCA: 18] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 56. | Acosta O, Bourgeat P, Zuluaga MA, Fripp J, Salvado O, Ourselin S. Automated voxel-based 3D cortical thickness measurement in a combined Lagrangian-Eulerian PDE approach using partial volume maps. Med Image Anal. 2009;13:730-743. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 79] [Cited by in RCA: 62] [Article Influence: 3.9] [Reference Citation Analysis (0)] |
| 57. | Aganj I, Sapiro G, Parikshak N, Madsen SK, Thompson PM. Measurement of cortical thickness from MRI by minimum line integrals on soft-classified tissue. Hum Brain Mapp. 2009;30:3188-3199. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 39] [Cited by in RCA: 33] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 58. | Cardoso MJ, Melbourne A, Kendall GS, Modat M, Hagmann CF, Robertson NJ, Marlow N, Ourselin S. Adaptive neonate brain segmentation. Med Image Comput Comput Assist Interv. 2011;14:378-386. [PubMed] |
| 59. | Leroy F, Mangin JF, Rousseau F, Glasel H, Hertz-Pannier L, Dubois J, Dehaene-Lambertz G. Atlas-free surface reconstruction of the cortical grey-white interface in infants. PLoS One. 2011;6:e27128. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 47] [Cited by in RCA: 48] [Article Influence: 3.4] [Reference Citation Analysis (0)] |
| 60. | Song T, Jamshidi MM, Lee RR, Huang M. A modified probabilistic neural network for partial volume segmentation in brain MR image. IEEE Trans Neural Netw. 2007;18:1424-1432. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 73] [Cited by in RCA: 73] [Article Influence: 4.3] [Reference Citation Analysis (0)] |
| 61. | Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, Rueckert D, Hajnal JV. Automatic segmentation and reconstruction of the cortex from neonatal MRI. Neuroimage. 2007;38:461-477. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 175] [Cited by in RCA: 127] [Article Influence: 7.1] [Reference Citation Analysis (0)] |
| 62. | Zhao L, Ruotsalainen U, Hirvonen J, Hietala J, Tohka J. Automatic cerebral and cerebellar hemisphere segmentation in 3D MRI: adaptive disconnection algorithm. Med Image Anal. 2010;14:360-372. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 24] [Cited by in RCA: 23] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 63. | Pepe A, Zhao L, Koikkalainen J, Hietala J, Ruotsalainen U, Tohka J. Automatic statistical shape analysis of cerebral asymmetry in 3D T1-weighted magnetic resonance images at vertex-level: application to neuroleptic-naïve schizophrenia. Magn Reson Imaging. 2013;31:676-687. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 19] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 64. | Hyde DE, Duffy FH, Warfield SK. Anisotropic partial volume CSF modeling for EEG source localization. Neuroimage. 2012;62:2161-2170. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 19] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 65. | Wu Y, Warfield SK, Tan IL, Wells WM, Meier DS, van Schijndel RA, Barkhof F, Guttmann CR. Automated segmentation of multiple sclerosis lesion subtypes with multichannel MRI. Neuroimage. 2006;32:1205-1215. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 101] [Cited by in RCA: 83] [Article Influence: 4.4] [Reference Citation Analysis (0)] |
| 66. | Li W, Tian J, Li E, Dai J. Robust unsupervised segmentation of infarct lesion from diffusion tensor MR images using multiscale statistical classification and partial volume voxel reclassification. Neuroimage. 2004;23:1507-1518. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 26] [Cited by in RCA: 23] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 67. | Meier DS, Guttmann CRG. Time-series analysis of mri intensity patterns in multiple sclerosis. Neuroimage. 2003;20:1193-1209. [RCA] [DOI] [Full Text] [Cited by in Crossref: 72] [Cited by in RCA: 63] [Article Influence: 2.9] [Reference Citation Analysis (0)] |
| 68. | Khademi A, Venetsanopoulos A, Moody AR. Robust white matter lesion segmentation in FLAIR MRI. IEEE Trans Biomed Eng. 2012;59:860-871. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 39] [Cited by in RCA: 30] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 69. | Wei X, Warfield SK, Zou KH, Wu Y, Li X, Guimond A, Mugler JP, Benson RR, Wolfson L, Weiner HL. Quantitative analysis of MRI signal abnormalities of brain white matter with high reproducibility and accuracy. J Magn Reson Imaging. 2002;15:203-209. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 98] [Cited by in RCA: 91] [Article Influence: 4.0] [Reference Citation Analysis (0)] |
| 70. | Ahlgren A, Wirestam R, Sthlberg F, Knutsson L. Automatic brain segmentation using fractional signal modeling of a multiple flip angle, spoiled gradient-recalled echo acquisition. MAGMA. 2014;In press. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 8] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 71. | West J, Warntjes JB, Lundberg P. Novel whole brain segmentation and volume estimation using quantitative MRI. Eur Radiol. 2012;22:998-1007. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 82] [Cited by in RCA: 83] [Article Influence: 5.9] [Reference Citation Analysis (0)] |
| 72. | West J, Blystad I, Engström M, Warntjes JB, Lundberg P. Application of quantitative MRI for brain tissue segmentation at 1.5 T and 3.0 T field strengths. PLoS One. 2013;8:e74795. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 44] [Cited by in RCA: 46] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 73. | Duyn JH. The future of ultra-high field MRI and fMRI for study of the human brain. Neuroimage. 2012;62:1241-1248. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 176] [Cited by in RCA: 178] [Article Influence: 12.7] [Reference Citation Analysis (0)] |
| 74. | Van Leemput K, Bakkour A, Benner T, Wiggins G, Wald LL, Augustinack J, Dickerson BC, Golland P, Fischl B. Automated segmentation of hippocampal subfields from ultra-high resolution in vivo MRI. Hippocampus. 2009;19:549-557. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 350] [Cited by in RCA: 335] [Article Influence: 20.9] [Reference Citation Analysis (0)] |