Published online Oct 18, 2013. doi: 10.5312/wjo.v4.i4.241
Revised: July 28, 2013
Accepted: August 17, 2013
Published online: October 18, 2013
Processing time: 145 Days and 17.6 Hours
Lumbar vertebral body (VB) fractures are increasingly common in an ageing population that is at greater risk of osteoporosis and metastasis. This review aims to identify different models, as alternatives to bone mineral density (BMD), which may be applied in order to predict VB failure load and fracture risk. The most representative models are those that take account of normal spinal kinetics and assess the contribution of the cortical shell to vertebral strength. Overall, predictive models for VB fracture risk should encompass a range of important parameters including BMD, geometric measures and patient-specific factors. As interventions like vertebroplasty increase in popularity for VB fracture treatment and prevention, such models are likely to play a significant role in the clinical decision-making process. More biomechanical research is required, however, to reduce the risks of post-operative adjacent VB fractures.
Core tip: Lumbar vertebral body (VB) fractures are increasingly common in an ageing population that is at greater risk of osteoporosis and metastasis. This review aims to identify different models, as alternatives to bone mineral density (BMD), which may be applied in order to predict VB failure load and fracture risk. The most representative models are those that take account of normal spinal kinetics and assess the contribution of the cortical shell to vertebral strength. Overall, predictive models for VB fracture risk should encompass a range of important parameters including BMD, geometric measures and patient-specific factors.
- Citation: Sisodia GB. Methods of predicting vertebral body fractures of the lumbar spine. World J Orthop 2013; 4(4): 241-247
- URL: https://www.wjgnet.com/2218-5836/full/v4/i4/241.htm
- DOI: https://dx.doi.org/10.5312/wjo.v4.i4.241
Lumbar vertebral body (VB) fractures, particularly in the osteoporotic or otherwise diseased spine, are a frequent cause of pain and reduced function amongst an ever-aging population. The treatment and prevention of such fractures has therefore gained increasing importance in recent years given the potential impact on healthcare and quality-of-life amongst the elderly.
Despite their prevalence, the aetiology of VB fractures remains relatively poorly understood; partly because only a relative minority have radiographically evident vertebral deformity and fail to gain medical attention; and partly because of the protracted onset of such fractures compared to limb injuries[1]. By far the most widespread cause is regarded to be osteoporosis-a skeletal disorder characterised by a generalised reduction in bone mass and deterioration of bone microarchitecture[2]-with VB compression fractures accounting for more than 45% of all osteoporotic fractures[3]. Consequently, the measure of bone mineral density (BMD) by techniques such as dual X-ray absorptiometry (DXA) and-to a lesser extent-quantitative computed tomography (QCT), has become the mainstay of clinical practice with regard to the diagnosis of osteoporosis and the prediction subsequent of VB fracture[4,5].
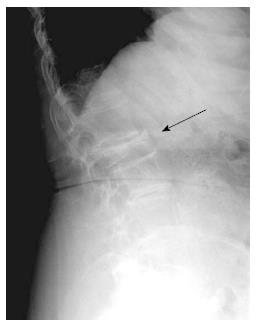
Fractures occur when the force applied to bone exceeds its load-bearing capacity. Hence, by causing a reduction in compressive strength of bone, osteoporosis typically increases the risk of VB fracture by way of either endplate failure and burst fracture, or more commonly by wedge compression fracture-as shown in Figure 1[1,6].
Forces acting on the lumbar spine can be substantial under physiological conditions with loads between 800 and 1200 N of axial compression being applied at L1 vertebra during upright standing[7]. Such compressive loads have been shown to increase vastly with forward bending particularly when combined with lifting-a5-fold increase has been observed with 45° of forward flexion whilst lifting 10 kg[1]. With their six degrees of freedom, functional spinal units (FSU) undergo motion other than just flexion under the action of a range of internal and external forces. However, as indicated, compressive forces associated with flexion and extension are the most important when considering the kinetics of the lumbar vertebrae. This arises from the observation that at static equilibrium the centre of mass of the upper torso, arms and head lies anterior to the axis of rotation found at L4/L5 or L5/S1 in the upright posture. The forward flexion moment generated is countered by the paraspinal muscles and subsequently the resultant vector acts to confer axial compression. Most biomechanical models, including both experimental and computational research, therefore aim to predict VB fracture by focussing on compressive forces.
Clearly, osteoporosis is not the only risk factor for VB failure. Pathological lesions produce discrete areas of vertebral weakness and subsequent fracture. In particular, the spine is the most frequent site of metastasis-such pathology has been reported in up to 80% of all cancer patients after death[7,8]. As is the case with osteoporosis, VB fractures associated with metastasis frequently produce vertebral collapse, deformity and subsequent pain. Deformity, be it within the (FSU) or the whole spinal segment, is believed to contribute to deleterious loading changes in the thoraco-lumbar spine. In the presence of VB wedge fracture(s) the loss of anterior vertebral height results in an increase in the flexion moment arm generated by the upper body, thereby increasing compressive loads and the propensity for further fracture[9]. More numerous fractures that produce a kyphotic segment of the spine can hasten abnormal biomechanics leading to a ‘‘vertebral fracture cascade’’[9]. In recent years, there has been an increase in the rates of surgical intervention for such patients, both as preventative and therapeutic measures[3]. The injection of bone cement into the VB-known as vertebroplasty-to restore strength and reduce pain is the foremost treatment currently, in terms of popularity and cost-effectiveness[3]. In spite of its advantages, however, vertebroplasty has been linked with several drawbacks based on both clinical and biomechanical grounds-most notably, an increased risk of adjacent VB fracture.
This review article focuses on biomechanical models that aim to predict the risk of failure load and fracture in the VBs of healthy spines and in those that harbour disease. The challenges that exist in the implementation of such risk models and in the use of vertebroplasty, are also described.
In principle, excessive loading and/or a reduction in VB strength result in fracture. Given that spinal loading is essentially an external driver and varies with different activities, it is necessary to determine VB strength in order that fracture risk can be assessed[10]. Although BMD has widespread clinical use and has been shown to predict vertebral fractures with a relative risk of 2.3 per standard deviation change[5], there exists much literature that expounds only a partial role of BMD in determining VB strength[10-12]. In engineering terms, the prediction of fracture risk is also dependent on vertebrae’s complex geometry, their elastoplasticity and structural heterogeneity[10]. As BMD can vary widely between those with and without VB fractures, it is a test that may be regarded as having poor sensitivity with respect to fracture thresholds[6,11]. Additionally, the interpretation of scans used to determine BMD clinically can be distorted by aortic calcification along with other artefacts[5]. Perhaps the most compelling limitation of BMD measurement as the sole predictor of fracture risk, is the fact that imaging techniques such as QCT generally fail to take into account the cortical shell of VBs, analysing only the spongy bone portion[2]. This is in spite of evidence suggesting that the best predictor of distal radius and proximal femur failure load is cortical bone geometry at the respective sites[4]. Hence, BMD estimation of both the spongiosa and the cortical shell is advocated, in addition to consideration of the cortical geometry when predicting VB strength[2,4].
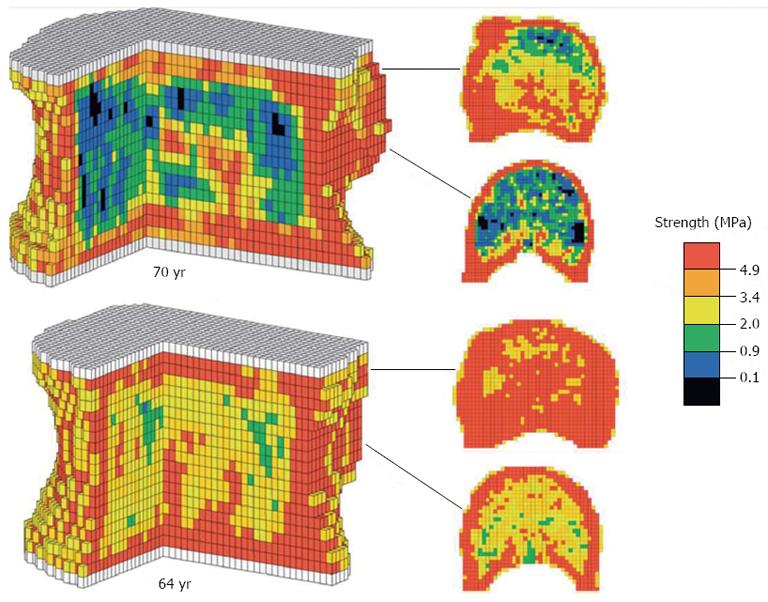
The contribution of cortical bone to the overall mechanical properties of vertebrae is gaining increasing attention, as variation in cortical BMD has been seen to follow patterns according to age and sex-related differences. Relative reductions in cortical BMD have been associated with increasing age and with women, highlighting at least two areas of concern[2]. Firstly, the BMD, structure and therefore the contribution to overall VB strength of the spongiosa and cortical shell are distinct. Hence, those QCT-based models that assume uniformity between the two constituents of the VB may be underestimating vertebral strength and overestimating fracture risk. Secondly, the age and sex-related differences in cortical BMD and structure, suggest that cortical bone goes through a process of change during which heterogeneity within the shell may be exhibited. Models using computer tomography (CT) systems of lower resolutions may fail to identify areas of demineralisation and in doing so misrepresent failure load. In contrast, however, it is also argued that unlike the thick cortices of long bones in the body, the VB cortical bone is much too thin for significant load-bearing-a view supported by studies demonstrating that VB failure loads were the same as the mean crushing strength of decorticated specimens of VB spongiosa[2].
In noting some of the shortcomings in the use of BMD as a predictor of VB fracture risk, it is necessary to consider alternative methods by which this might be achieved with greater reliability. QCT imaging of cadaveric spines has been widely employed as a basis of computational modelling techniques of analysing VB structure-e.g., finite element (FE) modelling which employs computer software programs to generate 3D representations of the VB, constituted from minute geometric shapes (Figures 2 and 3). In spite of such techniques, however, there is relatively little research predicting absolute VB failure loads. That which does exist has shown very strong correlations between predicted and observed yield loads (stress at which the bone begins to deform plastically) and fracture loads[10]. By evaluating more than just failure loads such analyses can be said to be more accurate, and findings suggest that QCT in this respect is a reliable technique of obtaining a geometric and architectural survey of VBs in order for fracture risk prediction. However, an important limitation of QCT is that it fails to take account of the material properties, e.g., elastic modulus, of VB bone, which means that such a system would fail to incorporate variability in bone stiffness in its fracture risk prediction. Additionally, most QCT systems lack the relatively higher resolution needed to decipher the heterogeneous properties of the VB’s cortical bone[10]. This potential source of error may underestimate cortical shell density and thus predicted VB strength values, particularly since it has been demonstrated that as the BMD of VB spongiosa reduces, load is increasingly transferred to the cortex[2].
A further noteworthy limitation of QCT-based VB fracture prediction arises from removal of the posterior elements of the vertebrae during loading tests. The ligaments, laminae and facet joints that make up the posterior elements are known to be load sharing structures and therefore their exclusion, in an attempt to reduce interference during VB CT imaging, can introduce inaccuracies when predicting in vivo VB fracture risk[10]. This may account for its relative lack of popularity in clinical practice as compared to its use in research and modelling. Despite the limitations of using QCT-based analytical models, their use does still demonstrate very strong correlations between predicted and measured VB strength[1].
The measurement of anterior vertebral height (AVH) is another parameter that offers potential as an independent predictor of VB failure and the use of lateral spinal radiographs is the gold standard method by which this is achieved. AVH evaluation has been shown to be significantly more accurate in diagnosing and predicting VB fractures than DXA-based BMD values for the lumbar vertebrae and indeed for the femoral neck[11]. A much greater risk (95.2%) of VB fracture is observed when the AVH is ≤ -2.5 SD amongst female patients. Such research has further made the case against BMD as a valid predictor of VB fracture risk, given that a third of women presenting with VB fracture possess normal BMD values, whilst a substantial group of patients free of fracture demonstrate BMD values ≤ -2.5 SD. Though the use of AVH in this way does not employ numerical or experimental methods to calculate VB failure loads or strength values, it clearly demonstrates the relevance of VB geometry to vertebral strength and the prediction of fracture risk.
Reductions in AVH can generally be regarded as a representation of VB wedging frequently observed in osteoporotic patients. Such deformity even with single fractures has been linked to deterioration in the physiologic kinetics of the spine-significantly greater flexion moments (> 15%) and shear forces (> 250%) have been noted[9]. The increased forces result from the tilting of VB endplates, increased Cobb angle and subsequent anterior translation of the upper body centre of mass. Spinal curvature, as a form of pathology in its own right and not just a consequence of osteoporosis, has been intimately linked to loading in static conditions and therefore even subtle, yet clinically insignificant deformity, can give rise to adverse loading and increased fracture risk[9]. For instance, when baseline and follow-up lateral patient radiographs are prospectively evaluated for any prevalent vertebral deformities or incident VB fractures, those with a single vertebra deformity are six times more likely to suffer an incident VB fracture than those without deformity[12]. This figure rises to a greater than 20-fold increase in fracture risk for those with three or more deformed vertebrae.
Fractures can also be classified according to the McCloskey-Kanis algorithm-which describes deformity as either ‘‘biconcave’’, ‘‘wedged’’ or ‘‘crushed’’ -and then further subdivided with regard to detailed height measurements. Models that include such information acknowledge shape and severity of deformity as independent (of BMD) predictors of VB fracture-the former being of greater importance (Table 1)[12]. In addition, they also predict that the highest risk of fracture is present amongst individuals in whom the prevalent deformities occur at T5-T7 and L1-L3. Notably, the use of such predictive models serves to highlight several additional issues of relevance: firstly, that not all types of deformity confer the same risk; secondly that global factors, e.g., age, and propensity to fall, must play a role as fracture determinants given that the whole spine is deemed to be at risk despite localized deformity; and lastly the importance of multi-level spinal segment studies which are more representative of in vivo conditions[13].
A widely used method of evaluating VB fracture risk in the clinical trial setting is that developed by Genant et al[14]. Like AVH, spinal deformity index (SDI) is a system that also involves a visual assessment of lateral spine radiographs but instead grades each vertebra between T4 and L4 as either normal, mild, moderate or severe depending on the percentage compression. This semi-quantitative index represents both the severity of VB compression and the number of levels affected. SDI has been shown to be significantly correlated with vertebral fracture risk in validation studies, which is in keeping with the widely-held view that previous VB fracture is one of the most important predictors of subsequent VB fracture[15]. An important issue that such systems do not address, however, is the risk of fracture in patients known to have osteoporosis but without a pre-existing fracture or associated deformity.
The key to reliable predictions of VB fracture load, it has been suggested, is in the combination of BMD and geometric parameters of the VB[6] -in particular vertebral strength being dependent on the product of bone density x endplate area. Thus, strength reduces with a decrease in either BMD or vertebral dimensions. Since vertebral geometry is known to vary between individuals, within an individual’s spine and indeed with time-an age-related 14% increase in vertebral cross-sectional area has been observed in women[5] -vertebral failure load may too vary widely and less predictably than some models might suggest. For instance, a large VB endplate may compensate for a relatively low BMD and vice versa, which in turn suggests that the use of BMD to exclusively characterise vertebral strength may be somewhat inaccurate.
Vertebral fracture assessment (VFA) has in recent years gained recognition as a method of estimating fracture risk, particularly in the elderly female population[16]. Dual-energy X-ray absorptiometry is employed to provide low dose radiation imaging of the lateral spine which in turn allows for vertebral fracture(s) and associated deformity to be identified along with BMD measurements. The combined information generated from VFA has been shown to be comparable to spinal radiographs with regard to its ability to predict incident vertebral fractures in elderly women, but with the advantages of lower radiation exposure and less expense[16]. An important area of concern for VFA, however, is the adequacy of upper thoracic spine imaging[17].
QCT is an alternative investigation that can also exploit data pertaining to both BMD and the geometry of VBs. The authors of one particular study took measurements of both BMD and endplate area of the L3 vertebra of 75 patients and subsequently applied regression formulae to calculate compressive strength[6]. The presence or absence of VB insufficiency fractures amongst the same patients was determined by conventional radiographs from T10 to L5. By relating fracture prevalence to compressive strength, the researchers identified three stratified risk groups. Most notably, strength values of less than 3 kN were linked to a fracture risk of virtually 100%, whilst for values above 5 kN the risk was practically zero. Such data and others like it, demonstrate that compressive strength or failure loads of VB are better parameters by which to define fracture risk thresholds, than is BMD alone[6,18].
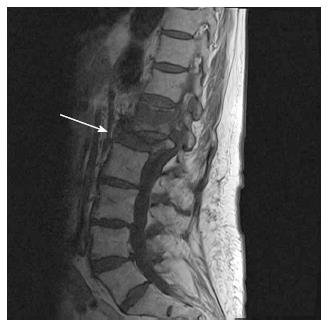
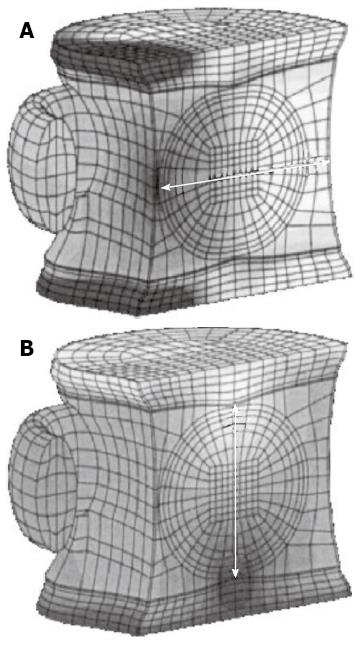
Metastasis arising from malignancy is another pathological process that afflicts the spine and impacts fracture risk. Fracture types frequently associated with such pathology are ‘‘burst’’ as well as wedge fractures and can occur under normal loading conditions[8]. Figure 3 demonstrates a lumbar burst fracture secondary to metastatic deposits. The proposed mechanism of burst fracture is believed to occur just prior or just subsequent to vertebral endplate failure. Experimentally validated FE modelling of metastatically involved motion segments (including the posterior arch) has suggested that patient-specific burst fracture risk is higher for those with increased tumour size, lower BMD, increased loads, and pedicle involvement[7]. Two further ‘biomechanical parameters have also been put forward-namely ‘‘vertebral bulge’’ and ‘‘vertebral displacement’’, which refer to compression-induced changes in VB width and height, respectively (Figure 4). Both measures have been shown to linearly correlate with cortical fracture strain threshold values, when under compressive loading conditions-although, the vertebral bulge equation has performed as the most accurate predictor (predictive power 100%), producing a clear threshold value for burst fractures[7,8].
In addition to the positive determinants of fracture risk prediction as seen in metastasis, degenerative disc disease has been identified as a factor that acts to reduce the risk of VB burst fracture[7]. Analytical and experimental models have demonstrated potential for their applicability in VB fracture risk prediction in the diseased spine. However, limitations and challenges to the widespread implementation of such models exist such as their lack of clinical validation. Also, like most others, these models fail to predict neurological injury-a tangible risk associated with burst fractures-which may consequently influence clinical decision-making. Finally, further assessment of multi-level spinal segments is required in order to provide a more representative prediction for fracture risk.
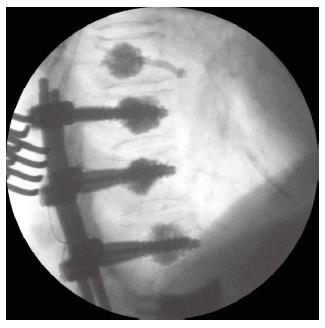
The ultimate purpose of models that predict vertebral fracture risk is to provide a rationale on which clinicians may base their decisions for intervention. Traditional conservative therapies have included bed rest, analgesia and bracing, whilst instrumented spinal stabilization was, until recently, the mainstay of surgical intervention[3]. Vertebroplasty, however, has gained increasing popularity over the last two decades acting in both preventative and therapeutic capacities. Vertebral augmentation with bone cement-most commonly polymethylmethacrylate (PMMA)-has provided early clinical improvement in regard to pain relief in more than 90% of cases[13] (Figure 5). Biomechanically, it serves to retain the normal vertebral and spinal geometry by increasing the VB stiffness and strength. But the procedure is not without risk. PMMA goes through an exothermic reaction which can cause neurological damage, localized inflammation and osteonecrosis[13]. There are also concerns regarding cement leakage, which can encroach into the spinal canal with disastrous consequences[3]. From a biomechanical standpoint the most significant complication is that of subsequent fracture in adjacent VBs. Some studies have noted a significant increase in the odds ratio of adjacent vertebral fractures before (1.44) and after (2.27) vertebroplasty, whilst others report that two thirds of new VB fractures occurred within the first 30 days of surgery[3].
Several potential mechanisms, by which adjacent fractures might occur following vertebroplasty, have been acknowledged. The rapid pain relief afforded by the procedure can allow for higher levels of physical activities, which are associated with greater risks of VB fracture. Alternatively, the fractures may occur merely as a consequence of the normal progression of osteoporosis and the fracture cascade that has been observed after the initial VB fracture[3]. Vertebroplasty (unlike kyphoplasty) does not restore normal geometry, namely vertebral height, after fracture and therefore the risks of subsequent fracture still exist due to suboptimal spinal kinetics, including the increased flexion moment arm.
Based on both experimental and computational studies, the ‘‘pillar’’ effect has been hypothesized to play an important role, whereby the relatively stiff augmented VB reduces and resists endplate bulge into it during axial compressive loading. The resultant increase in adjacent intradiscal pressure is transferred to the adjacent vertebra, thereby raising the risk of fracture here[3]. Despite conferring increased VB strength, vertebroplasty appears to reduce the overall strength of the FSU. Further biomechanical modeling and data is needed which may allow for modification of the material properties of cement.
Lumbar VB fractures are occurring with increasing frequency amongst an ageing population that is at greater risk of osteoporosis and metastasis. This article has served to demonstrate a number of models, as alternatives to BMD, which may be applied in order to predict VB failure load and subsequent risk of fracture. The conventional use of BMD and QCT has its limitations, such as the failure to incorporate the contribution of the cortex to overall VB strength and not only that of the spongiosa. Overall, predictive models for VB fracture risk should encompass a range of important parameters including BMD, geometric measures and patient-specific factors. As interventions like vertebroplasty increase in popularity, such models are likely to play a significant role in the clinical decision-making process.
P- Reviewers Abdellah El M, Benjamin G, Marco C S- Editor Zhai HH L- Editor A E- Editor Liu XM
| 1. | Bouxsein ML, Melton LJ, Riggs BL, Muller J, Atkinson EJ, Oberg AL, Robb RA, Camp JJ, Rouleau PA, McCollough CH. Age- and sex-specific differences in the factor of risk for vertebral fracture: a population-based study using QCT. J Bone Miner Res. 2006;21:1475-1482. [PubMed] |
| 2. | Andresen R, Werner HJ, Schober HC. Contribution of the cortical shell of vertebrae to mechanical behaviour of the lumbar vertebrae with implications for predicting fracture risk. Br J Radiol. 1998;71:759-765. [PubMed] |
| 3. | Baroud G, Vant C, Wilcox R. Long-term effects of vertebroplasty: adjacent vertebral fractures. J Long Term Eff Med Implants. 2006;16:265-280. [PubMed] |
| 4. | Augat P, Reeb H, Claes LE. Prediction of fracture load at different skeletal sites by geometric properties of the cortical shell. J Bone Miner Res. 1996;11:1356-1363. [PubMed] |
| 5. | Melton LJ, Riggs BL, Keaveny TM, Achenbach SJ, Hoffmann PF, Camp JJ, Rouleau PA, Bouxsein ML, Amin S, Atkinson EJ. Structural determinants of vertebral fracture risk. J Bone Miner Res. 2007;22:1885-1892. [PubMed] |
| 6. | Biggemann M, Hilweg D, Seidel S, Horst M, Brinckmann P. Risk of vertebral insufficiency fractures in relation to compressive strength predicted by quantitative computed tomography. Eur J Radiol. 1991;13:6-10. [PubMed] |
| 7. | Whyne CM, Hu SS, Lotz JC. Biomechanically derived guideline equations for burst fracture risk prediction in the metastatically involved spine. J Spinal Disord Tech. 2003;16:180-185. [PubMed] |
| 8. | Roth SE, Mousavi P, Finkelstein J, Chow E, Kreder H, Whyne CM. Metastatic burst fracture risk prediction using biomechanically based equations. Clin Orthop Relat Res. 2004;83-90. [PubMed] |
| 9. | Briggs AM, Wrigley TV, van Dieën JH, Phillips B, Lo SK, Greig AM, Bennell KL. The effect of osteoporotic vertebral fracture on predicted spinal loads in vivo. Eur Spine J. 2006;15:1785-1795. [PubMed] |
| 10. | Imai K, Ohnishi I, Bessho M, Nakamura K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine (Phila Pa 1976). 2006;31:1789-1794. [PubMed] |
| 11. | Diacinti D, Pisani D, Barone-Adesi F, Del Fiacco R, Minisola S, David V, Aliberti G, Mazzuoli GF. A new predictive index for vertebral fractures: the sum of the anterior vertebral body heights. Bone. 2010;46:768-773. [PubMed] |
| 12. | Lunt M, O’Neill TW, Felsenberg D, Reeve J, Kanis JA, Cooper C, Silman AJ. Characteristics of a prevalent vertebral deformity predict subsequent vertebral fracture: results from the European Prospective Osteoporosis Study (EPOS). Bone. 2003;33:505-513. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 4] [Reference Citation Analysis (0)] |
| 13. | Nouda S, Tomita S, Kin A, Kawahara K, Kinoshita M. Adjacent vertebral body fracture following vertebroplasty with polymethylmethacrylate or calcium phosphate cement: biomechanical evaluation of the cadaveric spine. Spine (Phila Pa 1976). 2009;34:2613-2618. [PubMed] |
| 14. | Genant HK, Wu CY, van Kuijk C, Nevitt MC. Vertebral fracture assessment using a semiquantitative technique. J Bone Miner Res. 1993;8:1137-1148. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2293] [Cited by in RCA: 2527] [Article Influence: 79.0] [Reference Citation Analysis (0)] |
| 15. | Crans GG, Genant HK, Krege JH. Prognostic utility of a semiquantitative spinal deformity index. Bone. 2005;37:175-179. [PubMed] |
| 16. | McCloskey EV, Vasireddy S, Threlkeld J, Eastaugh J, Parry A, Bonnet N, Beneton M, Kanis JA, Charlesworth D. Vertebral fracture assessment (VFA) with a densitometer predicts future fractures in elderly women unselected for osteoporosis. J Bone Miner Res. 2008;23:1561-1568. [PubMed] |
| 17. | Rea JA, Li J, Blake GM, Steiger P, Genant HK, Fogelman I. Visual assessment of vertebral deformity by X-ray absorptiometry: a highly predictive method to exclude vertebral deformity. Osteoporos Int. 2000;11:660-668. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 118] [Cited by in RCA: 103] [Article Influence: 4.1] [Reference Citation Analysis (0)] |
| 18. | Silva MJ, Keaveny TM, Hayes WC. Computed tomography-based finite element analysis predicts failure loads and fracture patterns for vertebral sections. J Orthop Res. 1998;16:300-308. [PubMed] |