Computer simulation of flow and mixing at the duodenal stump after gastric resection

Abstract

AIM: To investigate the flow and mixing at the duodenal stump after gastric resection, a computer simulation was implemented.

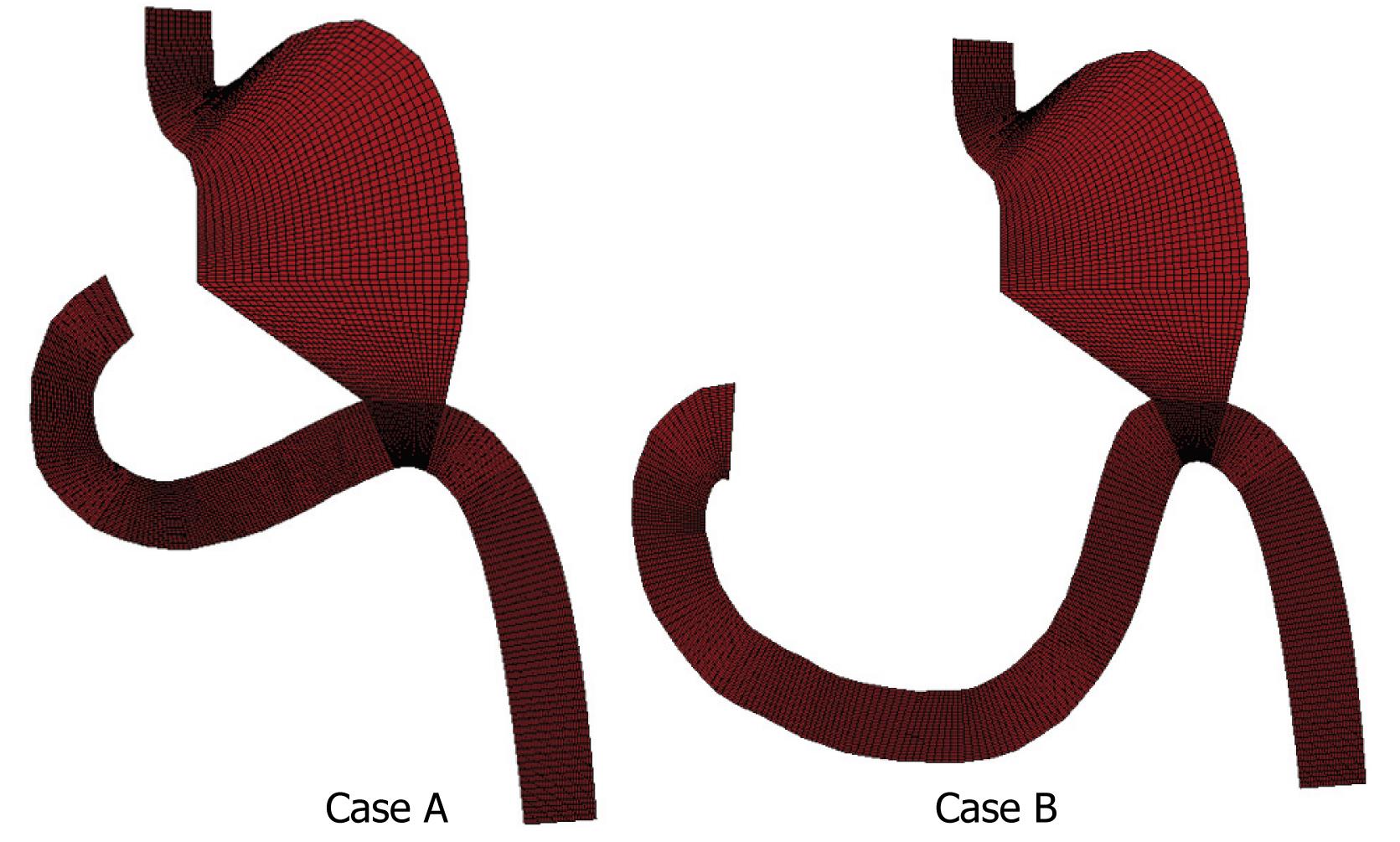
METHODS: Using the finite element method, two different Billroth II procedure cases (A and B) were modeled. Case A was defined with a shorter and almost straight duodenal section, while case B has a much longer and curved duodenal section. Velocity, pressure and food concentration distribution were determined and the numerical results were compared with experimental observations.

RESULTS: The pressure distribution obtained by numerical simulation was in the range of the recorded experimental results. Case A had a more favorable pressure distribution in comparison with case B. However, case B had better performance in terms of food transport because of more continual food distribution, as well as better emptying of the duodenal section.

CONCLUSION: This study offers insight into the transport process within the duodenal stump section after surgical intervention, which can be useful for future patient-specific predictions of a surgical outcome.

Key Words: Computer simulation; Gastric resection; Duodenal stump; Billroth II; Pressure distribution

INTRODUCTION

The duodenum is a short, complex and functionally highly specialized part of the small intestine. It has many motor, sensitive and secretory functions. Transit of chyme through the duodenum is a very complicated process (which includes intestinal peristalsis, gastric emptying, and pyloric sphincter tone) and is regulated by many neurological and hormone-dependent feedback mechanisms[1–6].

Two layers of smooth muscle cells (inner-longitudinal and internal-circumferential), as well as two neurological intramural networks (Auerbach’s and Meisner’s complexes), are responsible for gastroduodenal peristalsis. Electrical activity of the smooth muscle cell syncytium of the duodenum and in other parts of the gastrointestinal tract is represented by two basic types of electrical waves: slow waves and the spikes. Slow waves represent basic electrical activity and they are caused by activity of the Na-K pump. When the resting membrane potential become less negative than -40 mV, the spikes appear on the top of slow waves with a frequency of 1-10 Hz, and cause smooth muscle contraction. The number of duodenal contractions is about 12/min[7]. Several new investigations suggest that slow waves and spikes are regulated and spread through different cell networks[8].

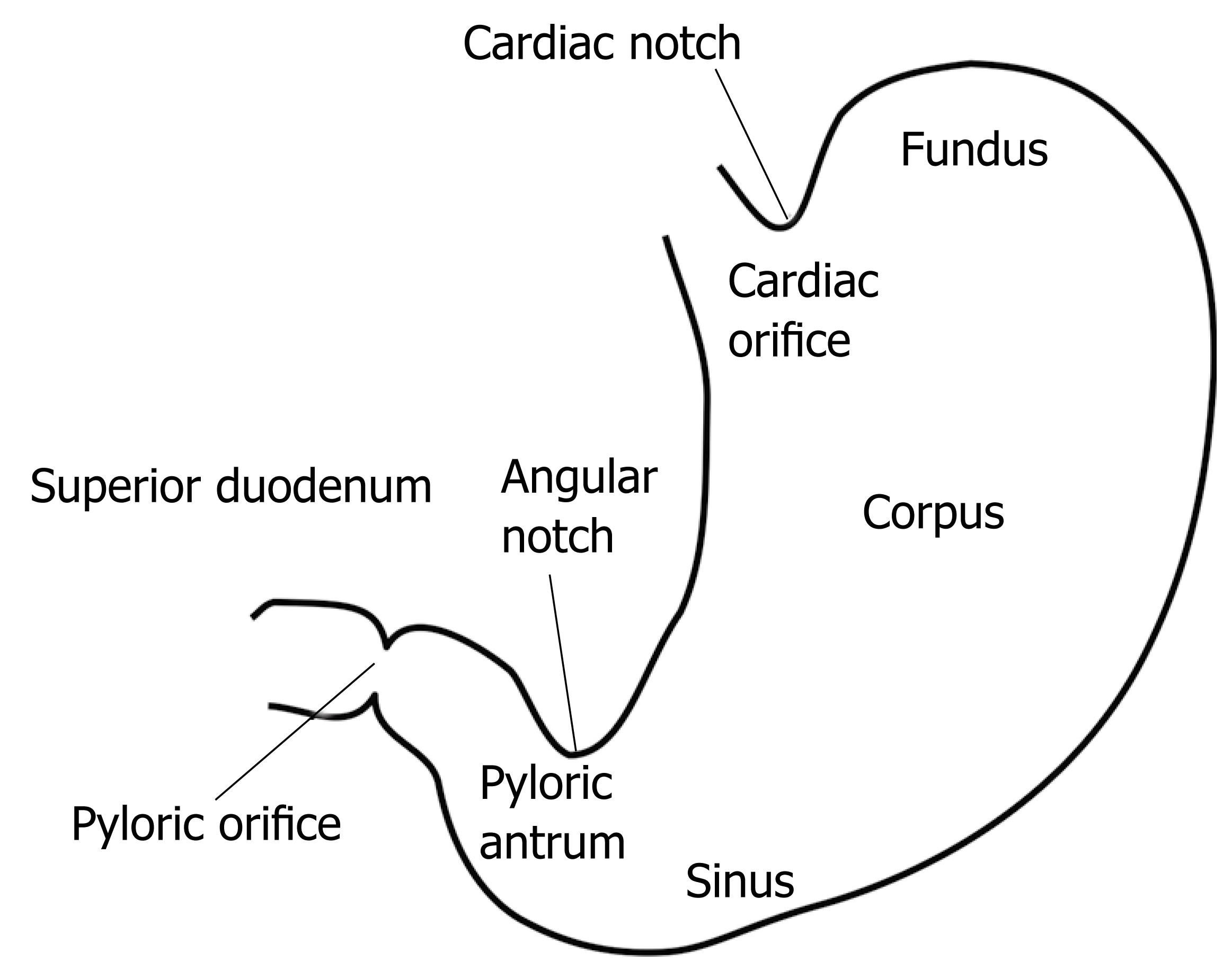
The pylorus shown in Figure 1 comprises a collection of tissue structures that connect the antrum to the duodenum. Its luminal diameter is controlled by a sphincter muscle complex that sets resistance to the bulk gastric effluent, through regulation of the pyloric orifice tone. During gastric digestion, the proximal and distal pyloric muscle loops occlude the pyloric lumen, preventing premature discharge of unprocessed material into the duodenum. Once the stomach has completed its task of breaking down large solid agglomerates into smaller particles, the pylorus relaxes and peristaltic contractions in the antrum begin to force chyme distally. At this point, antral contraction waves approach the pyloric orifice and, along with the sphincter complex and mucosal folds, cause steady constriction of the pyloric lumen. Chyme continues to be forcibly transported through this lumen until it is fully occluded, a process thought to induce an effluent jet into the superior duodenum[9]. Dysfunction of the duodenum can occur as a result of many disorders of gastric emptying and dyspeptic complaints, which demonstrates the vital role of the duodenum[10]. This role becomes especially apparent in surgical interventions on the gastroduodenum[11].

Figure 1 Normal physiological gastric outlet, pylorus, and superior duodenum.

A large number of studies have investigated the intact gastrointestinal tract anatomically[12–14], but there have been relatively few studies on the consequences of cutting muscles, nerves and other important anatomical structures of the gastroduodenum. These are unavoidable during surgical interventions, with disturbance of many fine, highly sophisticated feedback systems. These undesirable conditions lead to negative feedback mechanisms[1516] that cause changes in physiological processes with respect to the preoperative state[1718].

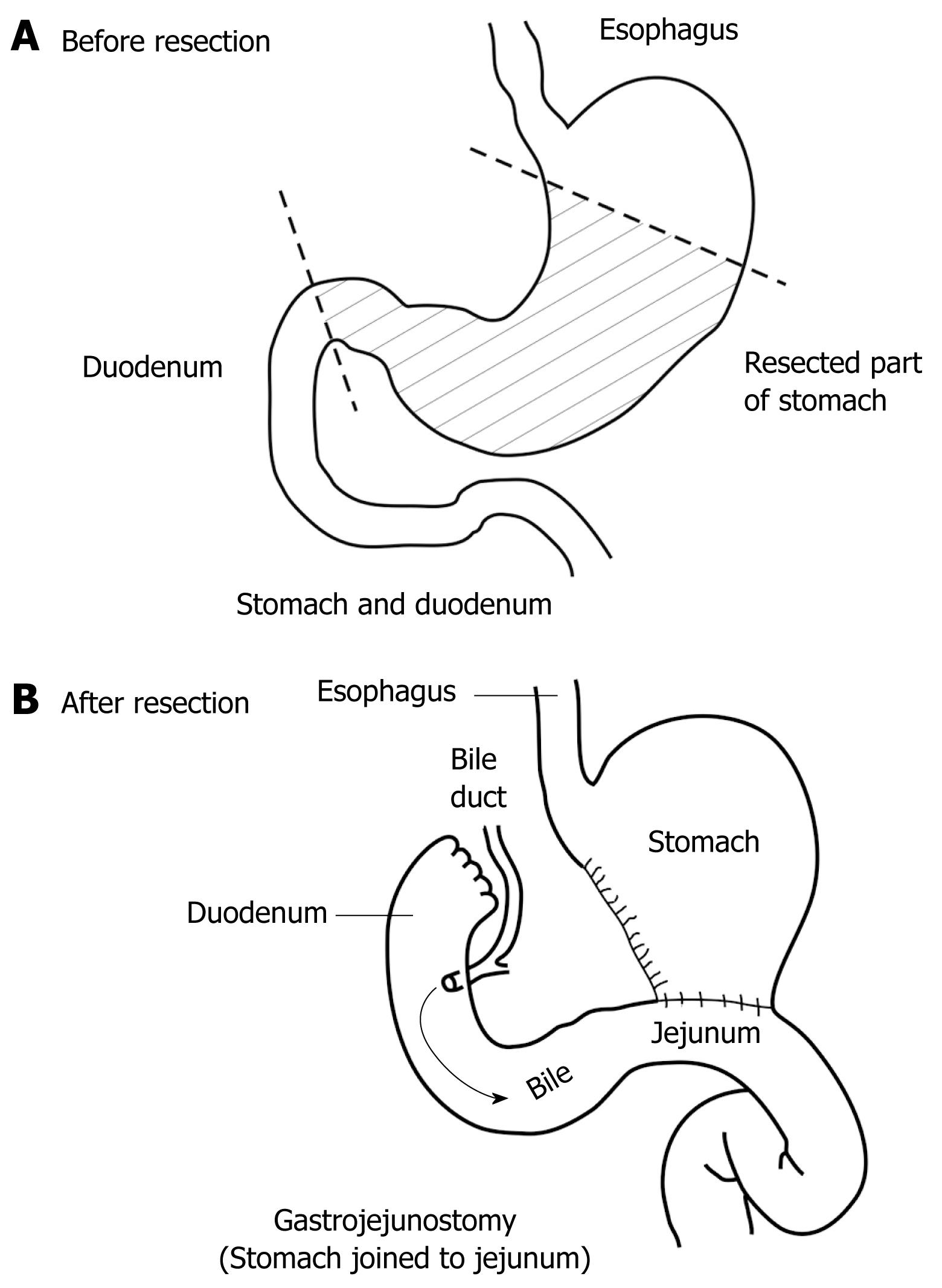
To date, it seems that insufficient attention has been paid to how the geometry and flow conditions affect the gastroduodenal system after distal gastric resection. There are various types of reconstruction of gastrointestinal continuity after gastric resection. In studying the treatment of gastric cancer, Devin reported in 1968 about 300 types of reconstruction after surgery of the gastroduodenal region[19]. During recent years, a few types have become more frequent. The first and most physiological variant is a state in which continuity of the gastrointestinal tract is reconstructed with anastomosis between the gastric stump and the duodenum; this procedure is called Billroth I gastric resection (gastroduodenal anastomosis). The other type of reconstruction is the Billroth II operation, which is shown in Figure 2, in which the anastomosis is located between the gastric stump and a loop of jejunum (gastrojejunal anastomosis, gut to side), and this type of intervention is the subject of our study. Anastomosis may include the entire circumference of the gastric stump (today it is a rarely used technique because of many unwanted consequences) or just a part of the circumference when a smaller diameter anastomosis is created. This is a better method of adaptation of the gastric stump and jejunal loop-the Hoffmeister-Finsterer modification. The length of the proximal jejunal loop is variable and depends on anatomical variations (e.g. length of the mesenterium of the small intestine, and adhesions), as well as surgeons’ ability. The jejunal loop conducts duodenal juice toward the gastric stump and the rest of the intestine. There is a hypothesis that increased intraluminal pressure in the afferent loop is the dominant cause of duodenal suture dehiscence (caused by the length of afferent jejunal loop, narrow gastrojejunoanastomosis, etc [20–22]). The distal or efferent loop is the part of the duodenum that is downstream of the anastomosis, and it conducts duodenal and gastric stump content distally to the small intestine. The anastomosis is antecolic when the jejeunal loop is positioned in front of the transverse colon, or the jejunal loop may be brought up posteriorly through an opening made in the transverse mesocolon (retrocolic anastomosis). Adequate position, shape and diameter of the anastomosis facilitate gastric emptying. The orientation of the jejunal loop may be two-fold, isoperistaltic, when the stomach and jejunum have the same peristalsis direction, and antiperistaltic, when the stomach and afferent loop of the jejunum have the opposite direction of peristalsis.

Figure 2 Schematic representation of reconstruction of gastrointestinal continuity after gastric resection. A: Normal anatomy of gastroduodenal region with resection lines; B: Billroth II antiperistaltic anastomosis.

There are other methods of gastrointestinal tract reconstruction after gastric resection, and one of these is called Roux en Y gastrojejunoanastomosis, in which the small bowel is cut distal to the ligament of Treitz, and the anastomosis is created between the distal limb of the jejunum and remaining gastric tissue (or esophagus in cases of total gastrectomy). The proximal limb of the jejunum is positioned downstream to the jejunum at a distance of about 45 cm, where a termino-lateral end-to-side anastomosis is created[2324].

In gastrointestinal tract reconstruction, the small bowel is not prepared to receive acidic content from the stomach, especially when duodenal juice is not present to neutralize it[25]. Suture dehiscence with postoperative peritonitis can occur as a complication after surgical intervention. Duodenal stump blowout is considered to be a serious postoperative complication, because of its high mortality rate[2627]. Suture dehiscence after surgical intervention in the gastroduodenal region has been the subject of many investigations, but still many pathological mechanisms involved in this surgical problem remain unclear[28].

This study offers a new approach to this problem. Using finite element analysis with computer modeling and clinical experiments, we attempted to determine physiological constants relevant to the above-mentioned surgical complication. In order to achieve this goal, we computed flow and mixing in the duodenal junction after distal gastric surgical resection and a Billroth II procedure.

MATERIALS AND METHODS

A prospective, randomized, placebo-controlled, multicenter study was performed on patients treated with Billroth II Hofmeister-Finsterer subtotal gastrectomy. Our task was to investigate and quantify the effects of increased intraluminal pressure in the duodenal stump on disruption of the duodenal suture.

Subjects

Measurements were performed on five patients after Billroth II Hofmeister-Finsterer surgical intervention. The indication for surgery was a malignant gastric process in three cases and ulcer disease in two. Patients with no significant co-morbidity were chosen for the study. Each patient gave written consent to our investigation. No complications were observed, and no complaints were made by these patients in relation to our actions for the purpose of this study.

Manometry equipment

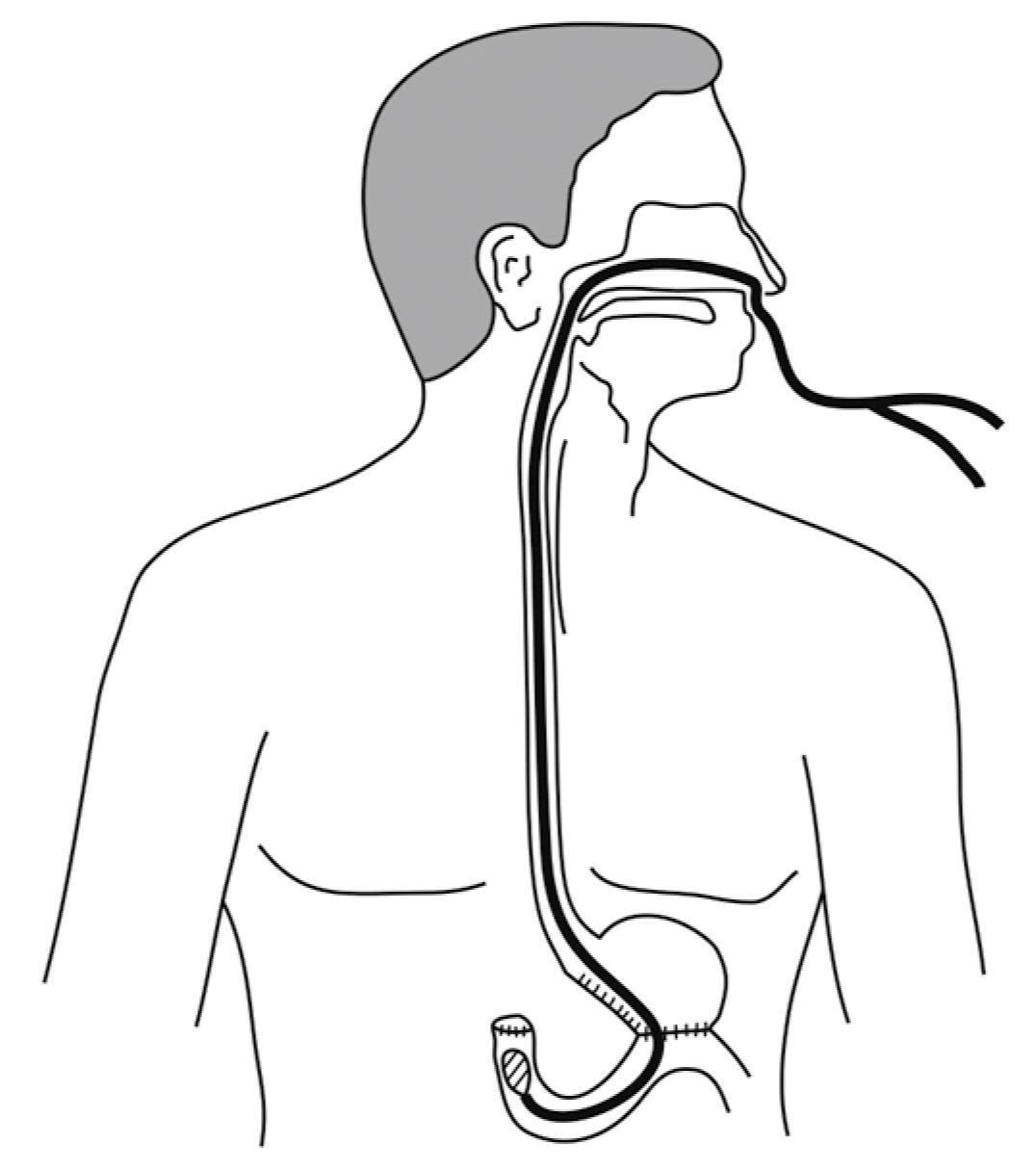
We created hardware and software equipment for measurement of pressure in the duodenal stump after distal gastric resection. The manometry assembly consisted of a Miller-Abbott tube, connecting catheters with control valves, transducers, analog-to-digital (AD) converter, and a computer with appropriate software. A Miller-Abbott tube 3.7 m in length, with an outer diameter of 5 mm, was placed in the duodenum after the operation (Figure 3). The volume of the balloon on top of the Miller-Abbott tube was 30 mL and the balloon expanded under pressure. The length of the balloon was 7 cm. The proximal end of the two-lumen tube was divided in two channels: one that connected the balloon with the measurement assembly of catheters, transducers, AD converter and personal computer; and the other used for aspiration of the duodenal stump. Distilled water was injected manually through the first channel into the balloon positioned in the duodenal stump. Data were recorded by an in-house developed software and stored to disk for later analysis. The measuring system was mobile and could be used outside the laboratory.

Figure 3 Schematic representation of the manometry equipment positioned in a patient during pressure measurement.

Protocol

The balloon of the Miller-Abbott tube was positioned at the duodenal bulb with minimum air insufflation, followed by direct visual control. The duodenum and anterior wall of the gastrojejunal anastomosis were sutured after appropriate placing of the balloon. The entire procedure lasted 3-5 min and did not have any influence on the operative procedure itself. The final location of the catheter was documented by checking X-rays before starting measurements and again before removal. Catheter migration from the duodenum was not observed. However, duodenal motility activity was noticed in two cases.

After the catheter was positioned and each subject was at rest for at least 24 h, all measurements were performed on patients in the supine position. Data files were recorded for each patient during seven postoperative days, starting 24 h after intervention. Data files consisted of pressure measurements over time. Prostigmine was used to stimulate bowel peristaltic movements. Every measurement lasted about 30 min. All external impacts that could cause some changes in duodenal intraluminal pressure were recorded in diagram form, as contractions of the anterior abdominal wall, cough, patient movements and administration of prostigmine.

Patients were discharged from the clinic after 10 d. They continue to be under observation and come to follow-up clinical examinations.

Details about the calculation of pressure inside the duodenal bulb using finite element fluid-solid analysis are as follows.

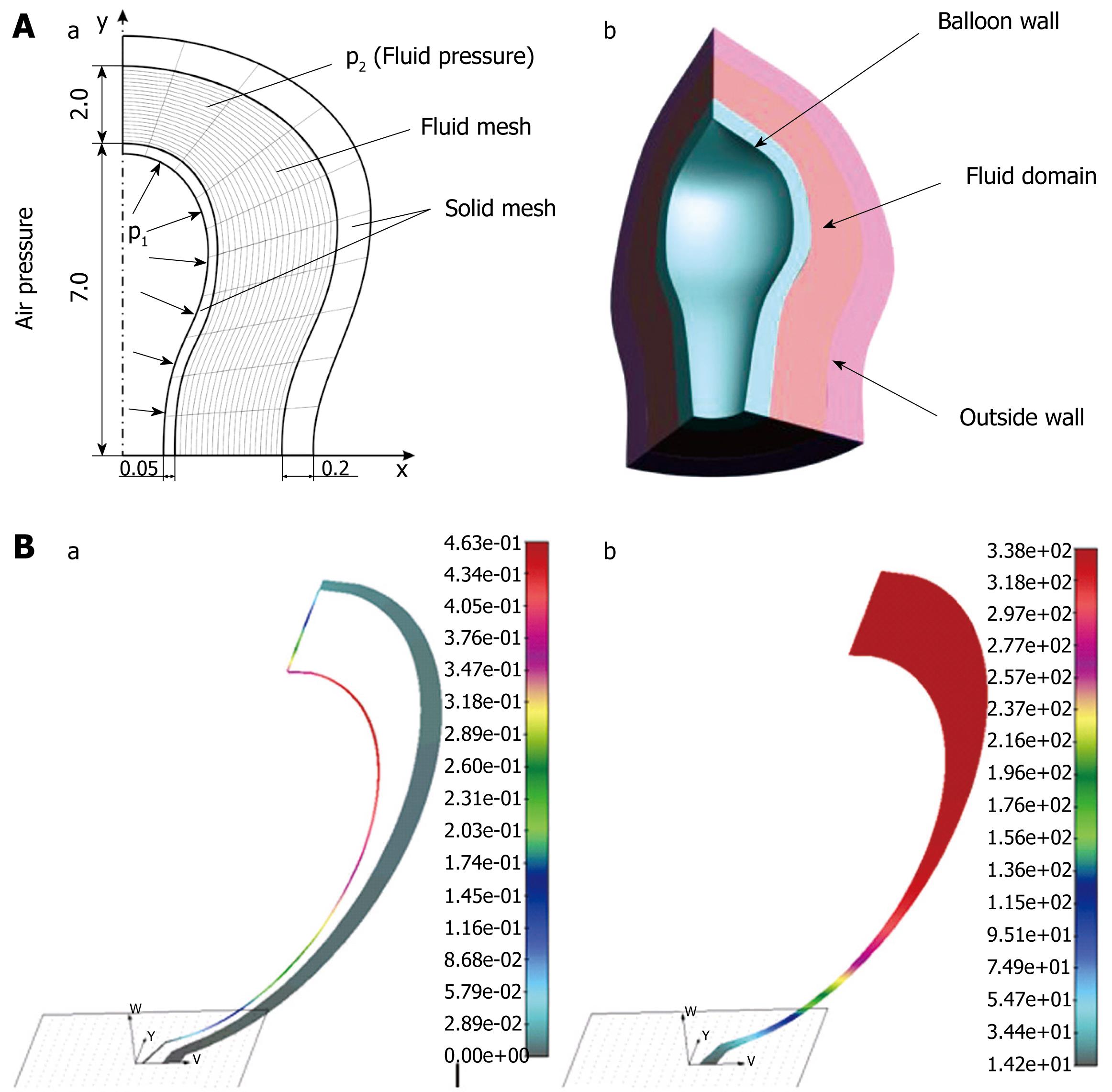
Computer simulation of pressure measurement inside duodenum bulb: We modeled balloon measurement of duodenal intraluminal pressure by using a finite element method[2930]. The balloon and the duodenal walls were discretized by 2D solid finite elements, while 2D fluid elements were used for the fluid domain (Figure 4A). A simplified axi-symmetric model was adopted. The thickness of the balloon wall was 0.05 cm and the outer wall was 0.2 cm. The length of the balloon was 7.0 cm, with a distance from the outer wall of 2.0 cm. Fluid density was taken as 1 g/cm³, dynamic viscosity &mgr; was 1000 cP, Young’s elasticity modulus E was 1 MPa. Fluid and solid domains had common boundaries at the interfaces on the balloon wall and duodenal wall. Air pressure was applied to the balloon wall, which caused flow of the fluid surrounding the balloon. The air pressure p₁ inside the balloon was measured, and the fluid pressure p₂ between the balloon and duodenal wall was calculated. The balloon deformed as a result of the difference between the air and fluid pressures. The deformed walls and fluid pressure distribution inside the duodenum are shown in Figure 4B. They corresponded to a maximum inlet balloon pressure of 2000 Pa (15 mmHg). The maximum balloon displacement was 0.4 cm, and the maximum fluid pressure within the duodenum was around 338 Pa (2.54 mmHg), which was in the physiological range.

Figure 4 Computer simulation of pressure measurement inside duodenum bulb. A: Schematic representation of the computational model of balloon pressure measurement inside the duodenum. Geometry of the model (a); 3D model view (b); B: Distribution of solid deformation (wall displacement) at the maximum pressure measurement (a); Fluid pressure distribution inside the duodenum (b).

Computational analysis

Computational analysis aimed to examine two different Billroth II antiperistaltic anastomosis cases. Case A represents gastric resection with a shorter and straight part of the duodenum, while case B, has a much longer and curved duodenal section. The geometry with finite element mesh for both cases is shown in Figure 5.

Figure 5 Geometry and finite element mesh of two selected cases. Case A showed a straight duodenal part with shorter length. Case B had a much longer and curved duodenal section.

A viscous incompressible fluid flow was considered here as the model for the transit of chyme. This flow is governed by the Navier-Stokes equations and continuity equation that can be written as[30]: (1) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \rho \left( {\frac{{\partial v_i }} {{\partial t}} + v_j \frac{{\partial v_i }} {{\partial x_j }}} \right) = - \frac{{\partial p}} {{\partial x_i }} + \mu \left( {\frac{{\partial ^2 v_i }} {{\partial x_j \partial x_j }} + \frac{{\partial ^2 v_j }} {{\partial x_j \partial x_i }}} \right) \] \end{document}

(2) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \frac{{\partial v_i }} {{\partial x_i }} = 0 \] \end{document}

where v_i is the chyme velocity in direction x_i (the coordinate axes are and ), ρ is the fluid density, p is pressure, &mgr; is the dynamic viscosity; and summation is implied on the repeated (dummy) indices, i,j = 1.2. The first equation represents balance of linear momentum, while equation (2) expresses incompressibility condition.

To take into account mass transport of food, we used the additional transport equation. The assumption is that the concentration of food does not affect the gastric fluid flow (i.e. a diluted mixture is considered). The food mass transport process is governed by the convection-diffusion equation, (3) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \frac{{\partial c}} {{\partial t}} + v_x \frac{{\partial c}} {{\partial x}} + v_y \frac{{\partial c}} {{\partial y}} = D\left( {\frac{{\partial ^2 c}} {{\partial x^2 }} + \frac{{\partial ^2 c}} {{\partial y^2 }}} \right) \] \end{document}

where c denotes the food concentration; v_x, v_y are the gastric velocity components in the coordinate system x, y; and D is the diffusion coefficient, assumed constant, of the transported food.

The code was validated using the analytical solution for shear stress and velocities through a straight tube[2930]. The finite element equations were solved with respect to velocities after the pressure was eliminated by a so-called penalty procedure. The solution was obtained by use of an incremental-iterative approach and implicit integration scheme over time. The system of algebraic equations of balance for a finite element, and for a time step and equilibrium iteration “m”, can be written as: (4) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \left[ {\begin{array}{*{20}c} {\frac{1} {{\Delta t}}{\mathbf{M}}_{\mathbf{v}} + {}^{t + \Delta t}{\mathbf{K}}_{{\mathbf{vv}}}^{\left( {m - 1} \right)} + {}^{t + \Delta t}{\mathbf{K}}_{\mu {\mathbf{v}}}^{\left( {m - 1} \right)} + {}^{t + \Delta t}{\mathbf{\hat K}}_{\mu {\mathbf{v}}}^{\left( {m - 1} \right)} + {}^{t + \Delta t}{\mathbf{J}}_{{\mathbf{vv}}}^{\left( {m - 1} \right)} + {\mathbf{K}}_{\lambda {\mathbf{v}}} } & {\mathbf{0}} \\ {{}^{t + \Delta t}{\mathbf{K}}_{cv}^{\left( {m - 1} \right)} } & {\frac{1} {{\Delta t}}{\mathbf{M}}_c + {}^{t + \Delta t}{\mathbf{K}}_{cc}^{\left( {m - 1} \right)} + {}^{t + \Delta t} {\mathbf{J}}_{cc}^{\left( {m - 1} \right)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\Delta {\mathbf{v}}^{\left( m \right)} } \\ {\Delta c^{\left( m \right)} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{}^{t + \Delta t}{\mathbf{\hat F}}_{\mathbf{v}}^{\left( {m - 1} \right)} } \\ {{}^{t + \Delta t}{\mathbf{F}}_c^{\left( {m - 1} \right)} } \\ \end{array} } \right\} \] \end{document}

where the detailed expressions for the matrices and vectors can be found elsewhere (e.g.[29–31]).

RESULTS

We here present typical results obtained by computer modeling and by our experimental investigation.

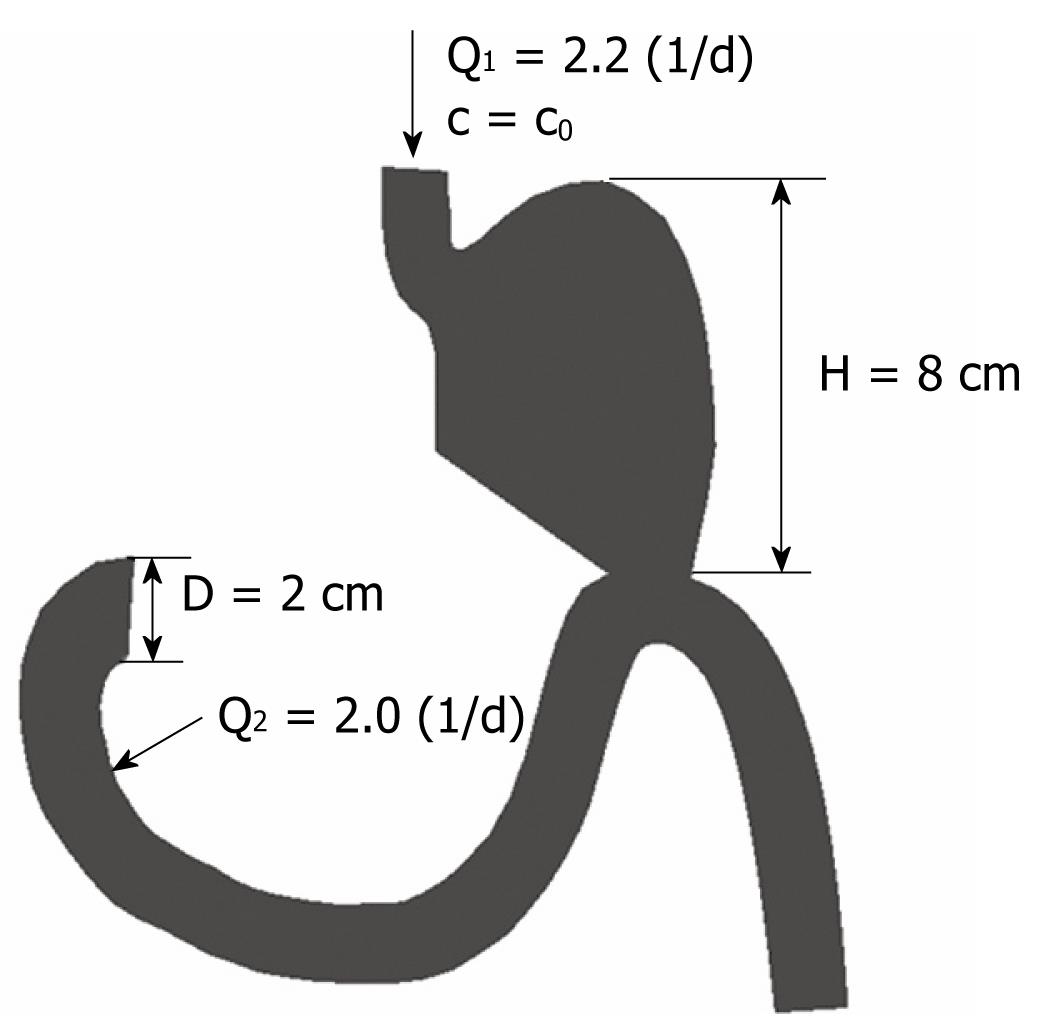
To examine different flow conditions, a few cases were considered within a simple 2D model. The steady state inflow conditions were imposed by specifying inlet fluxes at two different locations: gastric inlet with Q₁ = 2.2 (l/d) and duodenum inlet with Q₂ = 2.0 (l/d), as shown in Figure 6. These two flow conditions corresponded to a postoperative period of 3-4 d after distal gastric resection. Fluid density was taken as 1 g/cm³ and dynamic viscosity &mgr; was 1000 cP. For the convective-diffusion equation (3), boundary conditions were prescribed by the inlet food concentration c₀ = 1.0 (g/cm³).

Figure 6 Geometry and boundary conditions for a Billroth II Hoffmeister-Finsterer operation.

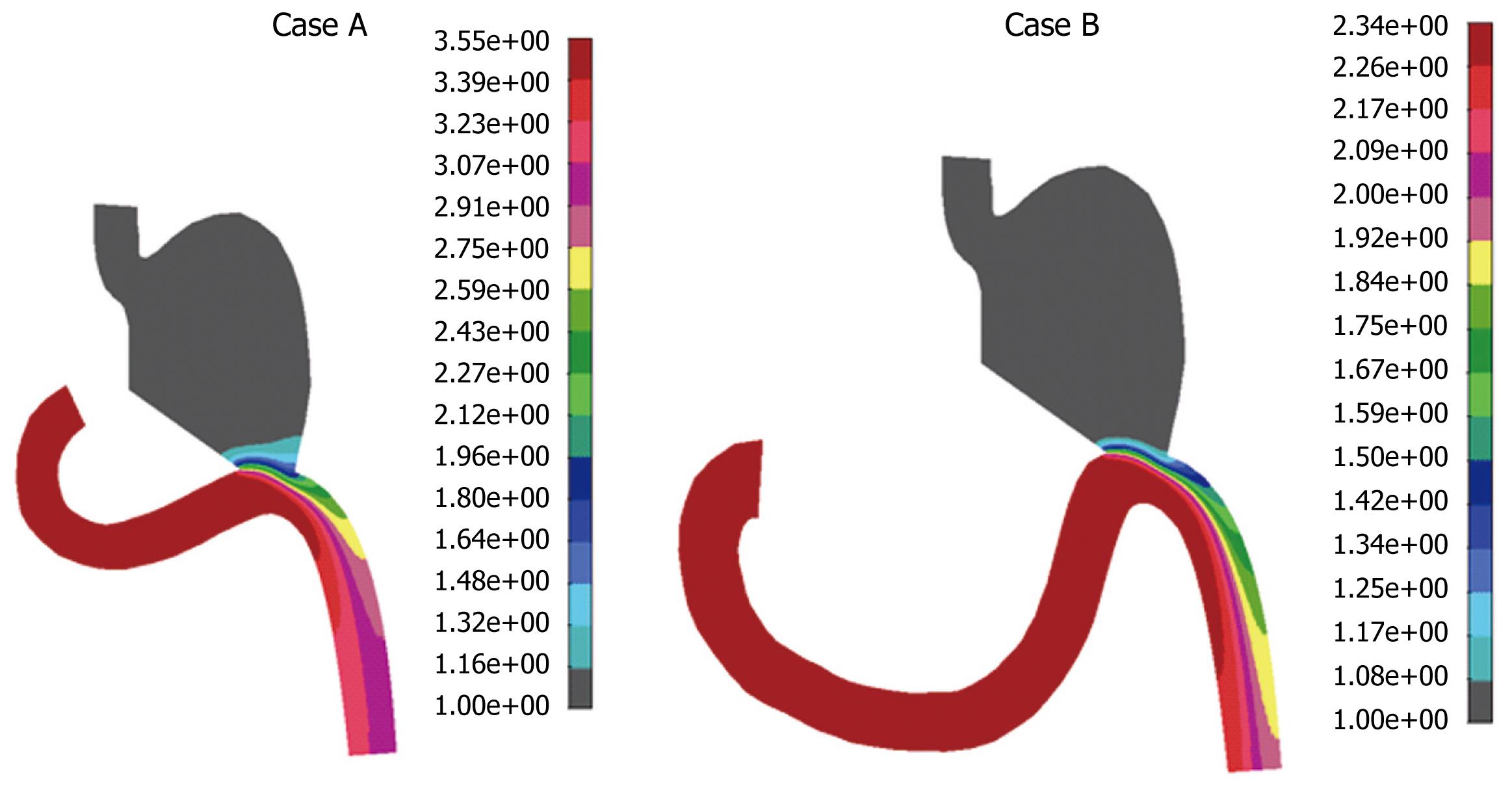
For the prescribed flow conditions at the inlets, steady state velocity distributions for both cases are shown in Figure 7. It can be seen that maximum velocity occurred at the inlet duodenal section, which was dominant during steady state flow conditions, such that fluid was moving distal to the remainder of the small intestine. Also, a maximum pressure (shown in Figure 8) was found near the pyloric section in the duodenal zone where the gastric resection was performed. Case B showed a higher pressure in comparison to case A, which was expected because of the longer section of duodenum in case B. This directly implies possible complications for case B because the risk of undesirable duodenal stump blowout was higher.

Figure 7 Velocity distribution for the steady state flow conditions [in (cm/s)].

Figure 8 Pressure distribution for the steady state flow conditions [in (mmHg)].

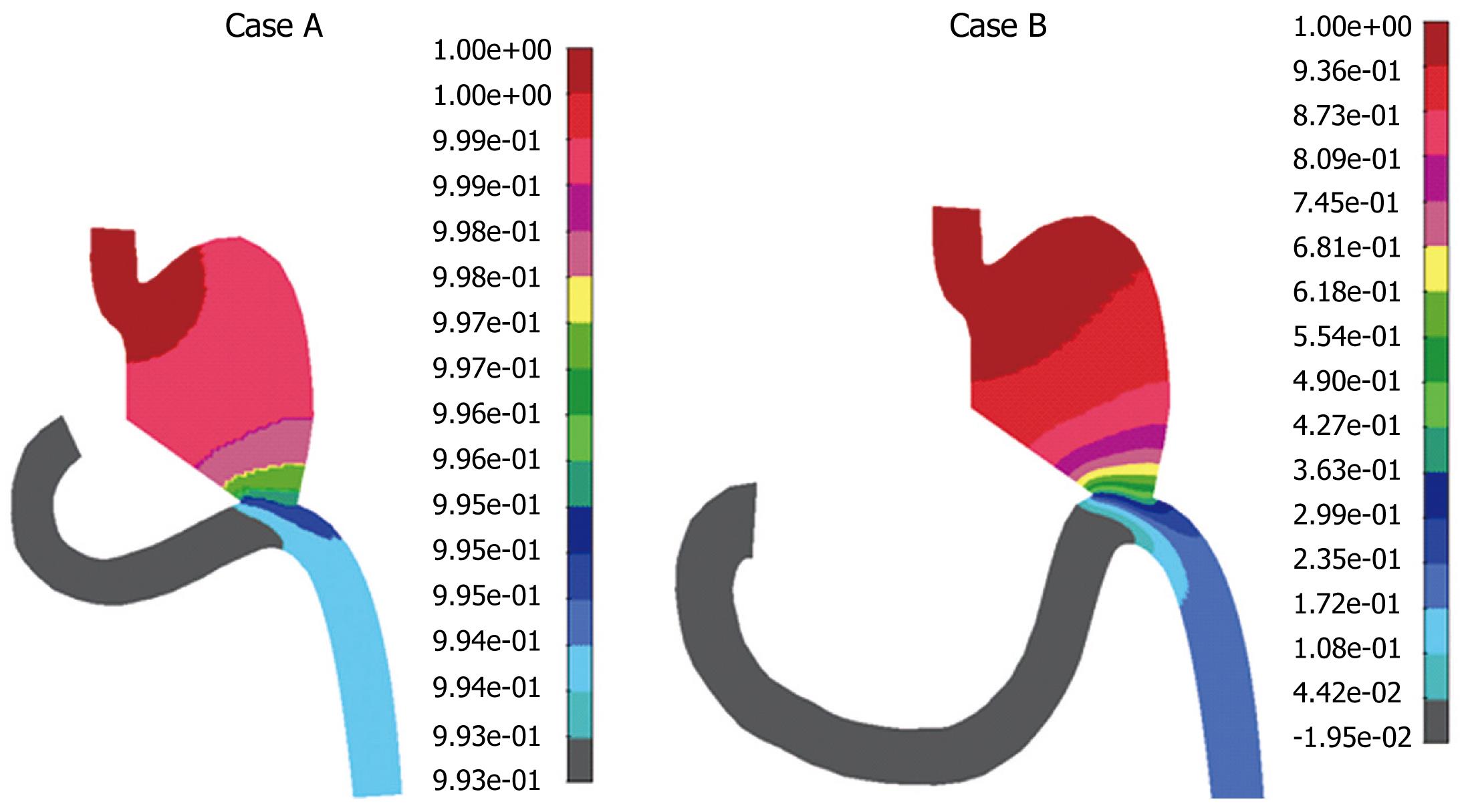
Mixing effect during postoperative period was examined by using mass transport analysis coupled with Navier-stokes equations. The influence of the diffusivity coefficient on the mass transport was investigated. Some authors[8] have suggested a negligible diffusivity which means that mass species simply advect along the fluid streamlines. Mass concentration distribution for the diffusion coefficient D = 2.0e-3 cm²/s for both cases A and B is presented in Figure 9. It can be seen from Figure 9 that maximal food concentration was located in the duodenal zone for both cases, which means that the food stays in this zone if the diffusion coefficient D is 2.0e-3 cm²/s. If the coefficient of diffusion is four times larger, at 8.0e-3 cm²/s, mass concentration distribution is different (Figure 10). Obviously, for the higher diffusivity coefficient (according to our analysis, D = 8.e-3 cm²/s) mass transport of food will go smoothly to the rest of gastrointestinal system, which is a desirable outcome. This effect of diffusivity is expected since diffusion enhances mass transport. There is also a difference in these two cases A and B, when the diffusivity is higher. It can be seen from Figure 9 that in case B, the duodenum section looked empty, while in case A there was approximately uniform mass distribution. This was probably the effect of the duodenal section. Therefore, the conditions in case B were better for the patient. A lower diffusivity coefficient D caused a more dominant convective term in equation (3), which resulted in food accumulation in the duodenal section. This is clearly shown in Figure 9, in which cases A and B had maximum food concentration in the duodenal zones. This means that a patient after this surgical procedure may have food accumulation in the duodenal zone, which is not desirable.

Figure 9 Mass concentration [in (g/cm³)] distribution for the diffusion coefficient D = 2. 0e-3 cm²/s.

Figure 10 Mass concentration [in (g/cm³)] distribution for the diffusion coefficient D = 8. 0e-3 cm²/s.

We tested cases A and B for D > 8.e-3 cm²/s (data not shown), for which computational analysis indicated a slightly better performance in the gastroduodenal connection for case A, for which more food passed through the duodenal zone.

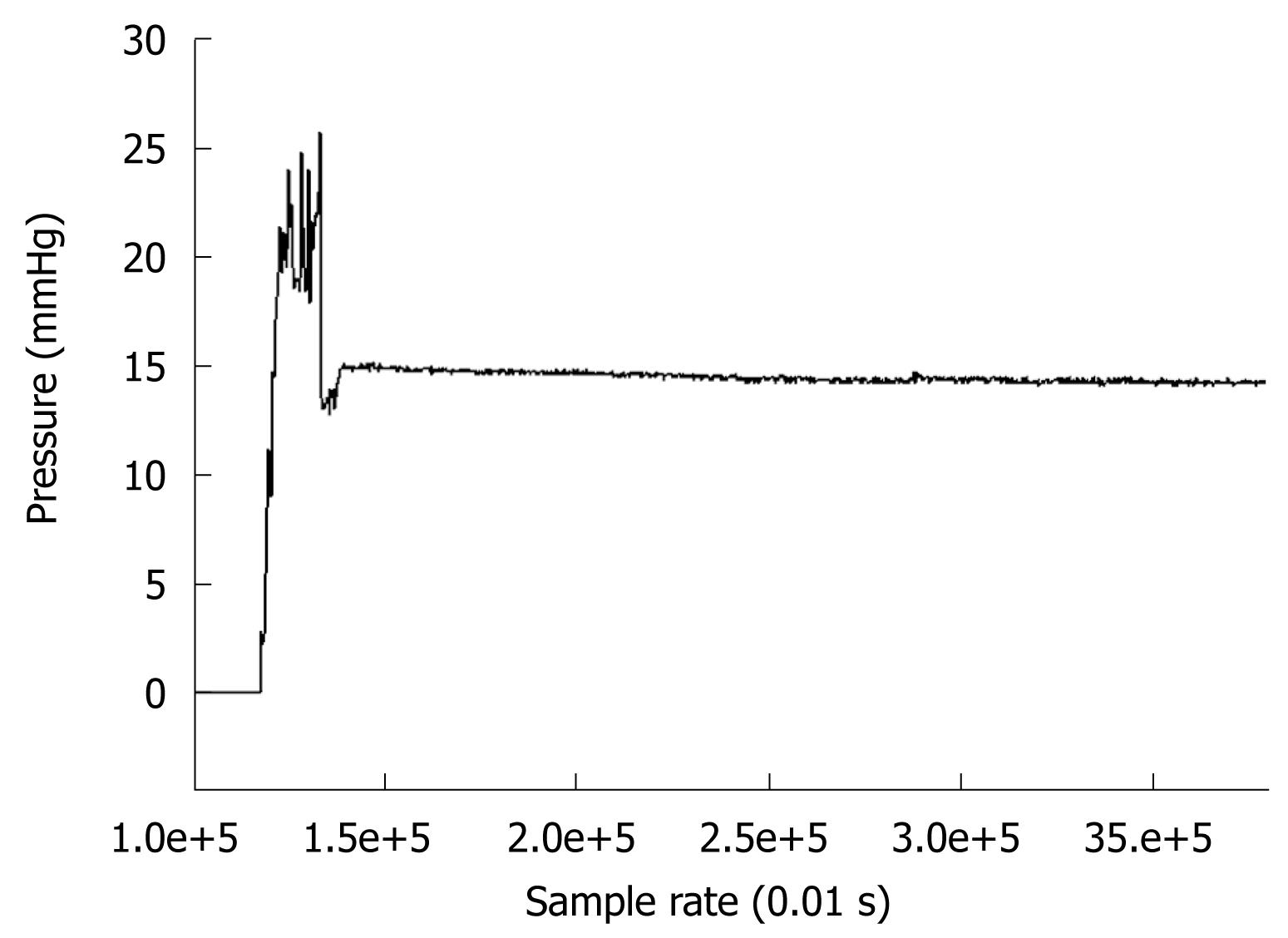
A measurement technique described in the Methods section and Appendix was implemented in order to measure pressure inside the duodenum a few days after surgical intervention. Patients agreed that this measurement technique could be used at 3-4 d after gastric resection. Among five patients, there was one with duodenal stump leakage, and one died from a non-surgical complication (pulmonary embolism). The contractile events associated with pressure changes were detected and recorded with our in-house software. We recorded pressure changes every 0.1 s. The pressure range shown in Figure 11 for the air inside the balloon was around 15 mmHg, while the fluid pressure inside the duodenum was between 3.5 and 4.5 mmHg (which was in the physiological range[32]). Also, numerical simulations (Figure 8) for cases A and B showed similar pressure distributions (around 2.5 mmHg).

Figure 11 Pressure measurement of Miller-Abbott (MA) tube and connecting catheter in the duodenum at 3 d after gastric resection.

DISCUSSION

The rate of postoperative gastric resection complication seems to be primarily influenced by increased duodenal pressure. Localization and extent of the malignant process, suture material, surgical technique, presence of potentially pathogenic microorganisms colonizing the digestive tract, and tissue quality, also may play a role in the pathogenesis of this complication[3334]. In this study, we focused on numerical simulation of two different Billroth II antiperistaltic anastomosis cases, with a slightly different geometrical connection of the duodenal and gastric parts during gastric resection. Numerical solutions of velocity and pressure distribution for both cases gave similar results. As expected, the maximum pressure was localized in the duodenal suture area and it was in the range of experimental pressure measurements obtained by using a Miller-Abbott tube and connecting catheter. Case B showed higher pressures, which was the result of the longer duodenal section.

Additional transport analysis showed that the food distribution in the gastric and duodenal connection zone varied depending on the diffusivity coefficient. The results of this analysis implied that case B was more favorable with respect to food transport because of continual food distribution and an empty duodenal section. Therefore, the longer duodenal section in case B provides conditions for food not to stay within the duodenal zone.

Experimental results have shown that intraluminal duodenal stump pressure after gastric resection was higher by an order of magnitude with respect to the pre-operative state. Comparison of models with different lengths of afferent loops showed that the afferent loop syndrome was an important factor in postoperative complications.

By changing input parameters of our interactive computational model (fluid parameters, model geometry), we can improve prediction of the potential in vivo events. Also, it is possible to obtain insight into possible outcomes of different types of surgical reconstruction of the digestive tract after operations on the gastroduodenal region. This may include variations of the same surgical intervention, related to surgeons’ ability or the specific anatomy of a single patient.

The practical aim of this study was to provide an insight into the physical conditions within the duodenal stump after gastric resection, in relation to the pathogenesis of duodenal stump blowout, and the implications for the surgical technique itself.

New, more comprehensive computational models may first include duodenal pressure quantification, which causes disruption of the duodenal stump closure. Such models will require determination of shear stress and pressure distribution at the inner surface of the duodenal stump, as well as the stress-strain state within the duodenal wall, especially in the suture area. The stress-strain state and the critical state at the point of disruption depend on tissue quality and tissue material characteristics. Furthermore, these sophisticated models need to establish a correlation between duodenal flow and the wall dynamics of contractions, in order to quantify critical levels of increased intraluminal duodenal pressure.

COMMENTS

Background

A malignant process and ulcer disease in the gastric distal section are the main causes for surgical intervention, which has become a standard procedure over recent years. Duodenal stump dehiscence after gastric resection occurs relatively rarely, but is of particular importance because it is associated with a high rate of mortality. A computer simulation can provide better understanding of this process.

Innovations and breakthroughs

Computer simulation offers better insight into fluid flow, mass transport and pressure distribution in the duodenal section before and after surgical intervention.

Applications

This computer simulation study can be applied to new follow-up studies that will help clinicians with diagnosis and treatment.

Terminology

Computer simulation and a finite element method solve a large number of equations in which physical laws such as fluid flow and mass transport are solved with differential partial equations. This methodology has been well known in industrial applications over several decades, and recently, it has been used for biological systems. Many questions regarding parameters in this computational study are still unknown and future computer simulation will try to answer these.

Peer review

The title describes well the manuscript. The introduction is clear. The description of the materials and methods is clear. The results are reported well. The discussion is well organized. The references are well reported. the tables and figures are clear.