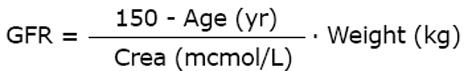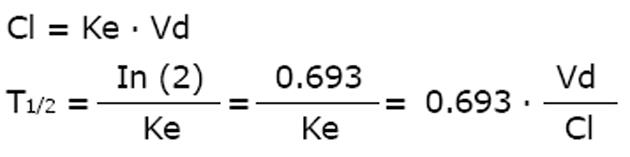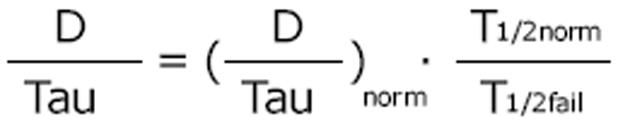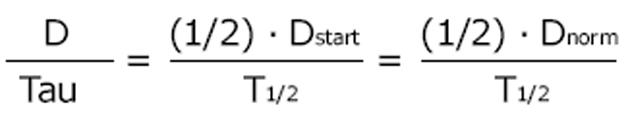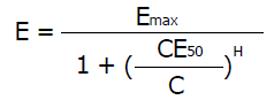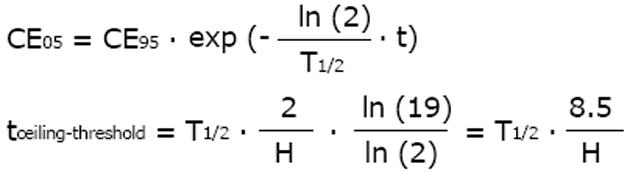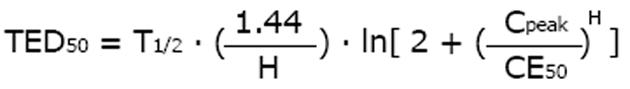Published online Jul 6, 2015. doi: 10.5527/wjn.v4.i3.330
Peer-review started: November 28, 2014
First decision: December 26, 2014
Revised: January 12, 2015
Accepted: May 5, 2015
Article in press: May 6, 2015
Published online: July 6, 2015
Processing time: 220 Days and 22.8 Hours
Patients with cancer have a high inherent risk of infectious complications. In addition, the incidence of acute and chronic kidney dysfunction rises in this population. Anti-infective drugs often require dosing modifications based on an estimate of kidney function, usually the glomerular filtration rate (GFR). However, there is still no preferential GFR formula to be used, and in acute kidney injury there is always a considerable time delay between true kidney function and estimated GFR. In most cases, the anti-infective therapy should start with an immediate and high loading dose. Pharmacokinetic as well as pharmacodynamic principles must be applied for further dose adjustment. Anti-infective drugs with time-dependent action should be given with the target of high trough concentrations (e.g., beta lactam antibiotics, penems, vancomycin, antiviral drugs). Anti-infective drugs with concentration-dependent action should be given with the target of high peak concentrations (e.g., aminoglycosides, daptomycin, colistin, quinolones). Our group created a pharmacokinetic database, called NEPharm, hat serves as a reference to obtain reliable dosing regimens of anti-infective drugs in kidney dysfunction as well as renal replacement therapy. To avoid the risk of either too low or too infrequent peak concentrations, we prefer the eliminated fraction rule for dose adjustment calculations.
Core tip: Cancer patients are at an increased risk for both infection and kidney dysfunction. Infections need immediate treatment; during the further course, kidney function must be taken into account. Almost any drug can be adjusted to any kidney function in every patient. Observation of the pharmacokinetic principles allows avoiding adverse events. Observation of the pharmacodynamic principles is needed to obtain anti-infective success. The target concentration for anti-infective drugs with a concentration-dependent effect is the high peak level. The target concentration for anti-infective drugs with a time-dependent effect is the high trough level. When in doubt, the peak should be the target.
- Citation: Keller F, Schröppel B, Ludwig U. Pharmacokinetic and pharmacodynamic considerations of antimicrobial drug therapy in cancer patients with kidney dysfunction. World J Nephrol 2015; 4(3): 330-344
- URL: https://www.wjgnet.com/2220-6124/full/v4/i3/330.htm
- DOI: https://dx.doi.org/10.5527/wjn.v4.i3.330
The number of patients requiring anticancer therapy is rising due to the increase in life expectancy. Presently, there is almost no malignancy without an option for either curative or palliative, adjuvant or neo-adjuvant chemotherapy. Anticancer drugs bear not only the risk of infection and “febrile neutropenia”[1] but also the risk of nephrotoxicity[2].
Acute kidney injury (AKI) of any cause is a known risk factor for and a consequence of infectious complications. AKI can also be potentiated by the nephrotoxicity of the chemotherapeutics. In cancer patients, the incidence of AKI is estimated at 15%-45% per year[3]. The prevalence of chronic kidney disease (CKD) is reported at 15%-50% in cancer patients[4,5]. This high prevalence can be due to demographic trends but in contrast to previous speculations, CKD is not a risk factor for non-renal malignancies[3].
This review addresses the pharmacokinetics and pharmacodynamics (PK-PD) of anti-infective therapies in cancer patients with impaired kidney function.
The therapeutic dilemma might be illustrated by the case of a 73-year-old female with fever and leukopenia. The diagnosis of multiple myeloma had been made 18 mo before admission. As a third-line chemotherapy, she had received 4 cycles of bendamustine and prednisolone. Now she was referred from another hospital because of acute on chronic kidney failure requiring hemodialysis (HD). After persistent fever while on piperacillin-combactam and radiological evidence of pneumonia, she received 1000 mg meropenem every 12 h as rescue therapy. Since the half-life was assumed to increase from 1.0 to 9.7 h, the administration interval was prolonged from 8 to 12 h (Table 1). The renal failure dose of 500 mg twice daily as recommended by the manufacturer was considered to be under-dosed - in agreement with recent publications[6]. She remained dialysis-dependent but could be discharged home 3 wk later.
| Drug | Half life | Loadingdose | Normal kidney function | Kidney impairment | Failure (GFR ≤5 mL/min) and hemodialysis | Hemofiltration (2 L/h) and continuous dialysis | ||||||
| (h) | (GFR = 100 mL/min) | (GFR about 30 mL/min) | Off dialysis day Dfail | DHD = Dfail + Dsup | ||||||||
| Normal | Failure | Dstart (mg) | Maintenancedose (mg) | Dose interval (h) | Maintenancedose (mg) | Dose interval (h) | Maintenancedose (mg) | Dose interval (h) | Post dialysis DHD (mg) | Maintenancedose (mg) | Dose interval (h) | |
| Abacavir (po) | 1.5 | 2.1 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | |||
| Aciclovir | 2.5 | 25 | 750 | 750 | 8 | 500 | 12 | 500 | 24 | 750 | 750 | 24 |
| Adefovir (po) | 1.6 | 160 | 10 | 10 | 24 | 10 | 48 | 10 | 168 | 10 | ||
| Albendazole (po) | 8 | 8 | 400 | 400 | 12 | 400 | 12 | 400 | 12 | |||
| Amantadine (iv) | 13 | 600 | 200 | 200 | 8 | 200 | 72 | 200 | 168 | 200 | 200 | 72 |
| (po) | 20 | 610 | 100 | 100 | 12 | 100 | 72 | 100 | 168 | 100 | ||
| Amikacin | 2 | 40 | Norm/Failure | 1500 | 24 | 500 | 24 | 250 | 24 | 750 | 750 | 24 |
| 1500/750 | ||||||||||||
| Amoxicillin (po) | 1.2 | 12 | 1000 | 1000 | 8 | 1000 | 12 | 500 | 12 | 1000 | ||
| Amoxicillin + Clavulanic acid | 1.2 + 1.2 | 12 + 4.3 | 500 + 125 | 500 + 125 | 8 | 500 + 125 | 12 | 500 + 125 | 12 | 500 + 125 | 500 + 125 | 12 |
| 875 + 125 | 875 + 125 | 8 | 875 + 125 | 12 | 500 + 125 | 12 | ||||||
| Amphotericin B | 24 (360) | 35 (360) | 70 | 70 | 24 | 70 | 24 | 50 | 24 | 50 | 50 | 24 |
| Amphotericin B liposomal | 24/92 | 24/160 | 200 | 200 | 24 | 200 | 48 | 200 | 24 | 200 | 200 | 24 |
| Ampicillin | 1 | 13 | 2000 | 2000 | 8 | 2000 | 12 | 1000 | 12 | 2000 | 2000 | 12 |
| + Sulbactam | + 1 | + 6.6 | + 1000 | + 1000 | 8 | + 1000 | 12 | + 500 | 12 | + 1000 | + 1000 | 12 |
| Amprenavir | 8 | 8 | 1200 | 1200 | 12 | 1200 | 12 | 1200 | 12 | |||
| Anidulafungin | 26 | 26 | 200 | 100 | 24 | 100 | 24 | 100 | 24 | 100 | 100 | 24 |
| Artesunate | 0.5 | 180 | ||||||||||
| Atazanavir (po) | 9 | 300 | 24 | |||||||||
| Atovaquone (po) | 63 | 63 | 750 | 750 | 12 | |||||||
| Atovaquone + | 63 | 63 | 250 + 100 | 250 + 100 | 24 | 250 + 100 | 24 | 250 + 100 | 24 | |||
| Proguanil (po) | 14 | 23 | ||||||||||
| Azidothymidine | 1 | 1.9 (52) | 200 | 200 | 8 | 100 | 8 | 100 | 8 | 200 | 200 | 24 |
| Azithromycin | 39 | 40 | 1000 | 500 | 24 | 500 | 24 | 500 | 24 | 500 | - | - |
| Brivudin (po) | 14 (144) | 125 | 125 | 24 for 7 d | ||||||||
| Caspofungin | 10 | 10 | 70 | 50 | 24 | 50 | 24 | 50 | 24 | 50 | 50 | 24 |
| Cefaclor (po) | 0.7 | 3 | 1000 | 1000 | 8 | 1000 | 12 | 1000 | 12 | 1000 | ||
| Cefazolin | 2.2 | 34 | 2000 | 2000 | 8 | 2000 | 12 | 500 | 12 | 1500 | 1000 | 12 |
| Cefotaxime | 1.2 | 7 (10) | 2000 | 2000 | 8 | 2000 | 12 | 1000 | 12 | 2000 | 2000 | 12 |
| Cefotiam | 1 | 8 | 2000 | 2000 | 8 | 2000 | 12 | 1000 | 12 | 2000 | 2000 | 12 |
| Ceftaroline fosamil | 2.7 | 6 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | 600 | 600 | 12 |
| Ceftobiprol-medocaril | 3.3 | 11 | 1000 | 1000 | 8 | 1000 | 12 | 500 | 12 | 1000 | 1000 | 12 |
| Ceftazidime | 2.1 | 25 | 2000 | 2000 | 8 | 2000 | 12 | 1000 | 24 | 2000 | 1000 | 12 |
| Ceftriaxone | 8 | 15 | 2000 | 2000 | 24 | 2000 | 24 | 2000 | 24 | 2000 | 2000 | 24 |
| Cefuroxime (iv) | 1.1 | 18 | 1500 | 1500 | 8 | 1500 | 12 | 750 | 24 | 1500 | 750 | 12 |
| (po) | 500 | 500 | 8 | 500 | 12 | 500 | 24 | |||||
| Chinin = Quinine | 13 | 15 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | 600 | 600 | 12 |
| Chloramphenicol | 2.5 | 7 | 1000 | 1000 | 8 | 1000 | 8 | 1000 | 12 | 1000 | 1000 | 12 |
| Chloroquine | 48/212 | 300 | 250 mg/8 h | 150 | 8 | 75 | 24 | |||||
| Cidofovir | 3.4 | 45 | 375 mg/168 h | 375 | 336 h = 14 d | 70 | 336 = 14 d | 35 | 336 = 14 d | 70 | 140 | 336 = 14 d |
| Ciprofloxacin (iv) | 4.4 | 10 | 400 | 400 | 12 | 400 | 12 | 400 | 24 | 400 | 400 | 12 |
| (po) | 500 | 500 | ||||||||||
| Clarithromycin | 6.8 | 17 | 500 | 500 | 12 | 500 | 12 | 500 | 24 | |||
| Clindamycin | 3 | 3 | 900 | 600 | 6 - 8 | 600 | 6 - 8 | 600 | 6 - 8 | 600 | 600 | 6 - 8 |
| Colistin colistimethate Na | 3 (9) | 24 (11) | 480 - 720 | 240 | 8 | 240 | 12 | 240 | 24 | 240 | 320 | 12 |
| = 7 Mio IE | = 3 Mio IE | = 3 Mio IE | = 3 Mio IE | = 3 Mio IE | = 4 Mio IE | |||||||
| Colistin (po) | 3 | 16 | 160 mg | 2 Mio IE | 12 | |||||||
| = 2 Mio IE | ||||||||||||
| Co-trimoxazole | 11/10 | 31/28 | 160/800 | 160/800 | 12 | 160/800 | 24 | 160/800 | 24 | 160/800 | 160/800 | 12 |
| Dalbavancin | 336 | 1000 | 500 | 168 | ||||||||
| Dapsone (po) | 24 | 31 | 200 | 200 | 24 | 200 | 24 | 200 | 24 | 200 | ||
| Daptomycin | 8 | 33 | 500 | 500 | 24 | 500 | 48 | 500 | 48 | 500 | 350 | 24 |
| 6-10 mg/kg | 6-10 mg/kg | 6-10 mg/kg | 6-10 mg/kg | |||||||||
| Darunavir (po) | 8 | 600 | 12 | |||||||||
| Delavirdine | 5.8 | 400 | 8 | |||||||||
| Didanosine (po) | 1.4 | 4.5 | 200 | 200 | 12 | 200 | 12 | 200 | 24 | |||
| Doripenem | 1 | 8 | 1000 | 1000 | 8 | 1000 | 8 | 1000 | 12 | 1000 | 1000 | 8 |
| Doxycycline | 15 | 23 | 200 | 100 | 24 | 100 | 24 | 100 | 24 | 100 | 100 | 24 |
| Efavirenz (po) | 46.8 | 47 | 600 | 600 | 24 | 600 | 24 | 600 | 24 | |||
| Emtricitabine (po) | 8.7 | 36 | 200 | 200 | 24 | 200 | 24 | 200 | 72 | |||
| Enfuvirtide | 30 | 90 | 12 | |||||||||
| Entecavir (po) | 24 (138) | 67 (384) | 1.0 | 1.0 | 24 | 0.5 | 48 | 0.5 | 72 | 0.5 | ||
| Ertapenem | 4.1 | 14.4 | 1000 | 1000 | 24 | 1000 | 24 | 1000 | 24 | 1000 | 1000 | 24 |
| Erythromycin | 2.3 | 5 | 1000 | 1000 | 8 | 1000 | 12 | 1000 | 12 | 1000 | 1000 | 8 |
| Ethambutol | 3.1 | 9.6 | 1600 | 1600 | 24 | 1200 | 24 | 1000 | 48 | 1600 | 1600 | 24 |
| 20 mg/kg | ||||||||||||
| Famciclovir (po) | 2.2 | 14 | 250 | 250 | 12 | 250 | 12 | 250 | 24 | |||
| Flucloxacillin | 0.8 | 3 | 2000 | 2000 | 8 | 2000 | 8 | 2000 | 8 | 2000 | 2000 | 8 |
| Fluconazole | 25 | 110 | 800 or 400 | 800 | 24 | 400 | 24 | 400 | 48 | 400 | 800 | 24 |
| Flucytosine | 4 | 150 | 2500 | 2500 | 6 | 2500 | 12 | 2500 | 48 | 2500 | 1250 | 24 |
| Fosamprenavir | 19 | 700 | 12 | |||||||||
| Foscarnet | 4.5 | 100 | 6000 | 6000 | 12 | 3000 | 24 | 3000 | 72 | 4000 | 3000 | 24 |
| 4000 | 8 | |||||||||||
| Fosfomycin (iv) | 1.5 | 20 | 5000 | 5000 | 8 | 5000 | 24 | 2500 | 24 | 5000 | 5000 | 12 |
| (po) | 3000 | single dose | ||||||||||
| Ganciclovir | 4.2 | 60 | 500 | 500 | 12 | 500 | 24 | 300 | 24 | 400 | 200 | 12 |
| 5 mg/kg KG | ||||||||||||
| Gentamicin | 2 | 48 | Norm/Fail | 240 | 24 | 120 | 24 | 40 | 24 | 120 | 120 | 24 |
| 240/120 | 0 | 48 | 320 before HD | |||||||||
| Hydroxy-chloroquine | 400 | 200 | 8 | |||||||||
| Imipenem/ | 0.9/ | 3.3/ | 1000 | 1000 | 8 | 1000 | 12 | 500 | 12 | 1000 | 1000 | 12 |
| + Cilastatin | 0.9 | 13.8 | ||||||||||
| Indinavir (po) | 1.8 | 2.1 | 800 | 800 | 8 | 800 | 8 | 800 | 8 | |||
| Isoniazid | 1/3.3 | 5/12 | 300 | 300 | 24 | 300 | 24 | 300 | 24 | 300 | 300 | 24 |
| Itraconazole (po) | 16 | 25 | 200 | 200 | 24 | 200 | 24 | 200 | 24 | 200 | ||
| Ketoconazole (po) | 3 | 2 | 200 | 200 | 12 | 200 | 12 | 200 | 12 | 200 | ||
| Lamivudine (po) | 6.2 | 21 | 150 | 150 | 12 | 150 | 24 | 100 | 24 | 150 | ||
| Levofloxacin | 7.3 | 35 | 750 | 500 | 12 | 500 | 24 | 250 | 24 | 500 | 500 | 12 |
| Linezolid | 4.9 | 6.9 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | 600 | 600 | 12 |
| Lopinavir/Ritonavir | 7/3.7 | 7/6.3 | 400 + 100 | 400 + 100 | 12 | 400 + 100 | 12 | 400 + 100 | 12 | |||
| Maraviroc (po) | 36 | 36 | 300 | 300 | 12 | 300 | 12 | 300 | 12 | |||
| Mebendazole (po) | 5 | 2 x 500 | 1000 | 8 | ||||||||
| Mefloquine (po) | 336 | 340 | 250 | 250 | 168 | 250 | 168 | 250 | 168 | |||
| Meropenem | 1 | 9.7 | 1000 | 1000 | 8 | 1000 | 12 | 1000 | 12 | 1000 | 1000 | 12 |
| Metronidazole (iv) | 10 | 11 (34) | 500 | 500 | 8 | 500 | 12 | 500 | 12 | 500 | 500 | 12 |
| (po) | 400 | 400 | 400 | 400 | ||||||||
| Micafungin | 13 | 14 | 100 | 100 | 24 | 100 | 24 | 100 | 24 | 100 | ||
| Miconazole | 24 | 24 | 1200 | 1200 | 24 | 1200 | 24 | 1200 | 24 | 1200 | ||
| Moxifloxacin | 12 | 15 | 400 | 400 | 24 | 400 | 24 | 400 | 24 | 400 | 400 | 24 |
| Nelfinavir (po) | 4.5 | 4 | 750 | 750 | 8 | 750 | 8 | 750 | 8 | |||
| Nitrofurantoin (po) | 1.0 | 1.2 | 100 | 100 | 8 | |||||||
| Nevirapine (po) | 28 | 22 | 200/24 | 200 | 12 | 200 | 12 | 200 | 12 | |||
| Oritavancin | 336 | 1200 | ||||||||||
| Oseltamivir (po) | 7 | (80) | 75 | 75 | 12 | 30 | 24 | 75 | 72 | 75 | ||
| Paromomycin | 2 | 40 | 500 | 8 | 500 | 24 | 500 | 48 | ||||
| Penicillin G = | 0.5 | 10 | 10 mega | 10 mega | 8 | 10 mega | 12 | 5 mega | 12 | 5 mega | 5 mega | 8 |
| Benzylpenicillin | ||||||||||||
| Penicillin V (po) | 0.6 | 4.1 | 1 mega | 1 mega | 8 | 1 mega | 8 | 1 mega | 12 | |||
| Pentamidine (iv) (inhaled) | 60 | 96 | 300 | 300 | 24 | 300 | 24 | 300 | 24 | |||
| 600 | 600 | 24 | ||||||||||
| 300 | 300 | 4 wk | ||||||||||
| Piperacillin | 1.1 | 4 | 4000 | 4000 | 8 | 4000 | 12 | 4000 | 12 | 4000 | 4000 | 12 |
| + Sulbactam | 1 | 8 | 500 | 500 | 8 | 500 | 12 | 500 | 12 | 500 | 500 | 12 |
| Piperacillin | 1.1 | 4 | 4000 | 4000 | 8 | 4000 | 12 | 4000 | 12 | 4000 | 4000 | 12 |
| + Tazobactam | 1 | 8 | 500 | 500 | 8 | 500 | 12 | 500 | 12 | 500 | 500 | 12 |
| Posaconazole (po) | 24 | 29 | 2 x 300 | 300 | 24 | 300 | 24 | 300 | 24 | |||
| Primaquine (po) | 6.3 | 6.4 | 30 | 30 | 24 | 30 | 24 | 30 | 24 | |||
| Proguanil (po) | 14 | 23 | 200 | 24 | ||||||||
| Propicillin (po) | 1 | 700 = 1 mega | 700 | 8 | ||||||||
| Prothionamide (po) | 1.5 | 1000 | 1000 | 24 | 500 | 24 | 250 | 24 | 500 | ? | ? | |
| Pyrazinamide (po) | 9.1 | 19 | 2000 | 2000 | 24 | 2000 | 24 | 2000 | 48 | 2000 | - | - |
| Pyrimethamine | 92 | 80 | 75 | 50 | 24 | 50 | 24 | 50 | 24 | |||
| Pyrvinium embonate | ? | ? | 50 | Single dosing | ||||||||
| Quinine | 13 | 15 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | 600 | 600 | 12 |
| Raltegravir (po) | 5.5 | 2.5 | 400 | 400 | 12 | 400 | 12 | 400 | 12 | |||
| Ribavirin aerosol | 44 | 26 | 6000 | 6000 | 12 | 6000 | 12 | 6000 | 12 | 6000 | 6000 | 12 |
| Ribavirin (po) | 4/250 | 24/672 | 600 | 600 | 12 | 400 | 24 | 200 | 24 | 400 | 400 | 72 |
| (iv) | 1000 | 1000 | 8 | 500 | 12 | 500 | 48 | 500 | 500 | 48 | ||
| Rifabutin (po) | 25 | 37 | 600 | 600 | 24 | 600 | 24 | 300 | 24 | |||
| Rifabutin + | 25 | 37 | 600 | 600 | 24 | 600 | 24 | 300 | 24 | |||
| Clarithromycin | 6.8 | 17 | 300 | 300 | 24 | 300 | 24 | 300 | 24 | |||
| Rifampicin (iv) | 4.5 | 4.5 | 600 | 600 | 24 | 600 | 24 | 600 | 24 | 600 | 600 | 24 |
| (po) | 450 | 450 | 12 | 450 | 12 | 450 | 12 | |||||
| Rifaximin (po) | intestine | unch | 400 | 400 | 12 | 400 | 12 | 400 | 12 | |||
| Ritonavir (po) | 3.7 | 6.3 | 600 | 600 | 12 | 600 | 12 | 600 | 12 | |||
| Roxithromycin | 12 | 15 | 300 | 300 | 24 | 300 | 24 | 300 | 24 | - | - | - |
| Saquinavir (po) | 7 | 13 | 2 x 500 | 1000 | 12 | 1000 | 12 | 600 | 12 | |||
| Stavudine (po) | 1.5 | 6.0 | 40 | 40 | 12 | 40 | 12 | 40 | 12 | 40 | ||
| Sofosbuvir | 1 (18) | (25) | 400 | 400 | 24 | 400 | 24 | 300 | 24 | 400 | ||
| Streptomycin | 2.6 | 100 | 1000 | 1000 | 24 | 500 | 48 | 250 | 72 | 250 | 500 | 24 |
| Teicoplanin | 52 | 348 | 3 x (800/24) | 1200 | 24 | 400 | 24 | 400 | 48 | 800 | 400 | 24 |
| Telavancin | 7.3 | 25 | 750 | 750 | 24 | 500 | 24 | 250 | 24 | 500 | 750 | 24 |
| Telbivudine (po) | 22 | 600 | 600 | 24 | ||||||||
| Tenofovir (po) | 14 | 28 | 245 | 245 | 24 | 245 | 24 | 245 | 48 | 245 | ||
| Terbinafine (po) | 16 | 16 | 250 | 250 | 24 | 250 | 24 | 250 | 24 | |||
| Tetracycline (po) | 8.9 | 83 | 500 | 500 | 8 | |||||||
| Tigecycline | 40 | 47 | 100 | 50 | 12 | 50 | 12 | 50 | 12 | 50 | 50 | 12 |
| Tipranavir (iv) | 2.8 | 2.8 | 500 | 500 | 12 | |||||||
| + Ritonavir (po) | 3.7 | 6.3 | + 200 | + 200 | ||||||||
| Tobramycin | 2 | 48 | Norm/Fail | 240 | 24 | 120 | 24 | 40 | 24 | 120 | 120 | 24 |
| 240/120 | ||||||||||||
| Trimethoprim (iv) (po) | 11 | 31 | 200 | 150 | 12 | 150 | 24 | 150 | 24 | - | - | - |
| 100 | 100 | 24 | 100 | 24 | ||||||||
| Trimethoprim + | 11 | 31 | 160 | 160 | 12 | 160 | 24 | 160 | 24 | 160 | 160 | 12 |
| Sulfamethoxazole | 10 | 28 | + 800 | + 800 | 12 | + 800 | 24 | + 800 | 24 | + 800 | + 800 | 12 |
| Trimethoprim + | 11 | 31 | 400 | 400 | 8 | 320 | 12 | 400 | 24 | 400 | 400 | 12 |
| Sulfamethoxazole | 10 | 28 | + 2000 | + 2000 | 8 | + 1600 | 12 | + 2000 | 24 | + 2000 | + 2000 | 12 |
| (Pneumocystis) | ||||||||||||
| Valacyclovir (po) | 2.5 | 25 | 1000 | 1000 | 8 | 1000 | 12 | 500 | 24 | 1000 | ||
| Valganciclovir (po) | 3.0 | 68 | 900 | 900 | 12 | 450 | 24 | 450 | 72 | 900 | ||
| Vancomycin | 6 | 150 | 1000 | 1000 | 12 | 1000 | 24 | 500 | 72 | 1000 | 1000 | 24 |
| Voriconazole | 8 | 12 | 2 x 400/24 | 200 | 12 | 200 | 12 | 200 | 12 | 200 | 200 | 12 |
| Zalcitabine (po) | 1.8 | 11 | 0.75 | 0.75 | 8 | 0.75 | 12 | 0.75 | 24 | |||
| Zanamivir | 2.5 | 13.7 | 10 | 10 | 12 | 10 | 12 | 10 | 12 | 10 | 24 | |
| Zidovudine | 1 | 1.9 (52) | 200 | 200 | 8 | 100 | 8 | 100 | 8 | 200 | 200 | 12 |
Anti-infective treatment is given with a therapeutic or a prophylactic indication. The preemptive treatment is distinguished from the induction therapy and the empirical differs from the sequential mode of therapy. For any mode of treatment, adjustment of anti-infective drug dose to the kidney function is recommended based on estimates of glomerular filtration rate (GFR) as well as pharmacokinetic and pharmacodynamic principles.
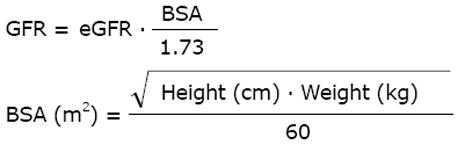
The kidney function can be measured by the GFR as this quantitates the primary and principal function of the nephron. It is an anachronism to use the endogenous creatinine clearance since urine collection errors are frequent[7]. This makes such estimates unreliable, resulting in under-dosing of anti-infective and anticancer drugs. For classifying the kidney dysfunction into one of the 5 stages of CKD, the standardized chronic kidney disease epidemiology collaboration (CKD-EPI) formula is currently preferred[8]. For drug dose adjustment, the GFR estimate easiest to access is the most appropriate[9]. Both, the modification of diet in renal disease (MDRD) or CKD-EPI equations estimate the GFR (eGFR) for a standard 1.73 m2 body surface area (BSA). To estimate the BSA, we use the Mosteller formula[10].
Math 8
The eGFR value is automatically calculated in most laboratories with the standardized MDRD and the CKD-EPI equations. Weight or body surface area are important determinants of the distribution volume and thus of the dose. Since oncologists are familiar with the use of BSA, the MDRD and CKD-EPI GFR might have advantages for dose adjustment calculations.
In the Cockcroft and Gault (C and G) formula the body weight is considered; it originally estimated the creatinine clearance. Like the other creatinine-based formulas, the C and G equation can also be used as an estimate of the GFR for drug dose adjustments[11]. Luzius Dettli proposed a coefficient-free version of the C and G equation[12] that was validated recently with the new calibrated serum creatinine measurements[13].
Math 9
Since the GFR is the independent and the serum creatinine is the dependent variable, there can be a time lag of 1 to 2 d behind the actual true kidney function and all creatinine-based GFR estimates in acute kidney injury (AKI). An interesting extension, therefore, is the so-called kinetic GFR for increasing and decreasing kidney function in patients with AKI[14]. The published equation can be derived from the C and G equation and rearranged for readily available measurements of the initial serum creatinine (Crea0) and differences (deltaX) between subsequent creatinine values (Crea1,2 ...).
Math 10
This approach holds for changing creatinine and is based on creatinine production. It relates the increase in serum creatinine within a specified time interval to the maximum increase in creatinine within one day. Since creatinine production and renal excretion is constant at about 1000 mg/d and the creatinine distribution volume is 42 L, the maximum 24 h increase in serum creatinine is 182 μmol/L if GFR is zero (the original publication says 133 μmol/L). If AKI is progressing and the creatinine is increasing, the above 1 - deltaX term is < 1.0 whereas the 1 - deltaX term is > 1.0 for decreasing creatinine values and restitution of AKI. The kinetic GFR estimate makes the general GFR-based dose adjustment rules (see below) also applicable to AKI and the intensive care condition with renal replacement therapy[14].
The main pharmacokinetic parameters are clearance, volume and half-life. Malcolm Rowland claimed the primacy for the clearance term since elimination is driven by clearance not half-life[15]. Where clearance reflects a mechanistic model, however, the half-life reflects a mathematical approach. Friedrich Hartmut Dost argued that the clearance estimate depends on bioavailability and body weight - as does the volume as well - whereas half-life does not[16].
There is a close relationship between the three parameters of clearance (Cl), volume (Vd) and half-life (T1/2) where the half-life is inversely proportional to the elimination rate constant (Ke).
Math 11
As discussed for antiviral drugs, the half-life is the pharmacokinetic parameter that most impacts drug action[17]. Since the half-life indicates how long an administration interval should be selected, and since the duration of drug action is correlated to the half-life, we consider the elimination half-life to be the most useful pharmacokinetic parameter for drug dosing[18]. In some cases the special half-life that represents the largest part of the area under the curve should be considered - Luzius Dettli coined it the “dominant half-life”. Generally, the effect-indicative half-life at target concentrations should be used for dose calculations[18].
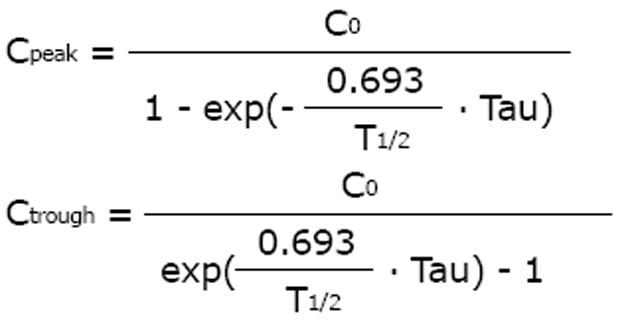
An increase and prolongation of the half-life was first reported by Kunin et al[19] for special drugs in patients with impaired kidney function. If the half-life is prolonged, drug accumulation kinetics will produce higher peak and higher trough concentrations with an increased risk for drug toxicity. According to the accumulation kinetics, the steady-state peak (Cpeak) and the trough concentrations (Ctrough) depend on the initial concentration after the first dose (C0), on half-life (T1/2) and administration interval (Tau).
Math 12
The relation between kidney function and half-life is as complex and hyperbolic as that between GFR and serum creatinine. It was a great advantage for drug dose adjustment that Luzius Dettli demonstrated the linear relationship between drug elimination and kidney function. This dependence was originally described as a linear function between the elimination rate constant and the creatinine clearance[20]. The modern approach describes this dependence as a linear function between drug clearance (Cl) and GFR.
Math 13
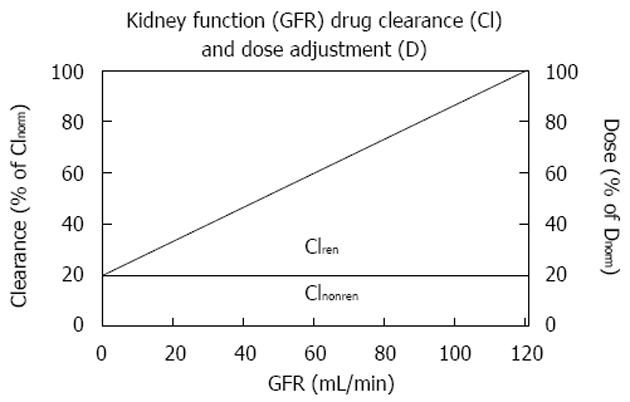
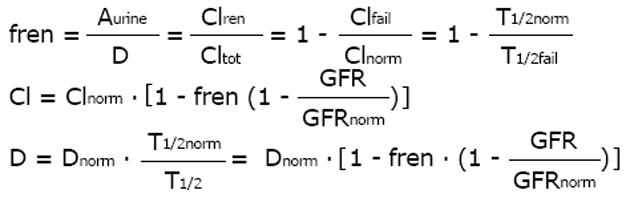
Based on this fundamental equation, the dose can be adjusted to the individual GFR in proportion to the decrease in drug clearance (Figure 1). The dose can also be adjusted in inverse proportion to the increase in half-life since in many published investigations, the inverse half-life, namely the elimination rate constant (Ke) has been related to the GFR. Based on the ideas of Luzius Dettli and for practical purposes, the fraction eliminated by the renal route (fren) has been proposed as the leading parameter for drug dose adjustment[21].
Math 14
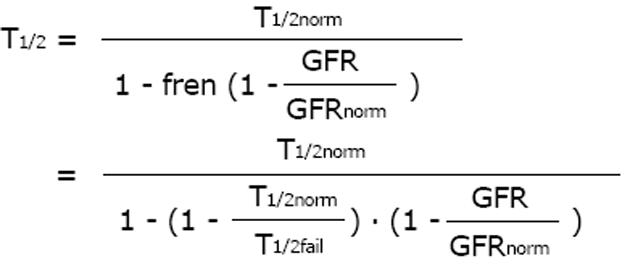
Since pharmacokinetics of anticancer drugs is rarely investigated in patients with CKD or AKI, it is an advantage that this fraction can be derived in volunteers with normal kidney function. However, kidney dysfunction also influences non-renal clearance, bioavailability and drug metabolism by the liver and intestines[22]. Therefore, the pharmacokinetics as determined in real patients with failing kidney function (CKD or AKI) should be the preferred source for drug dose adjustment calculations (e.g., half-life estimates).
Math 15
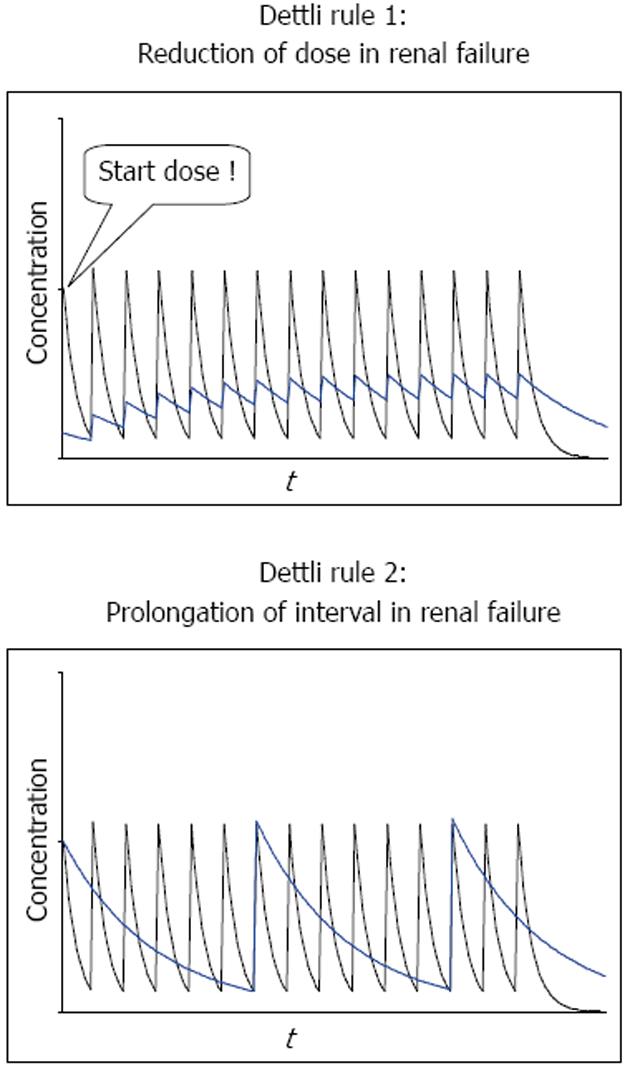
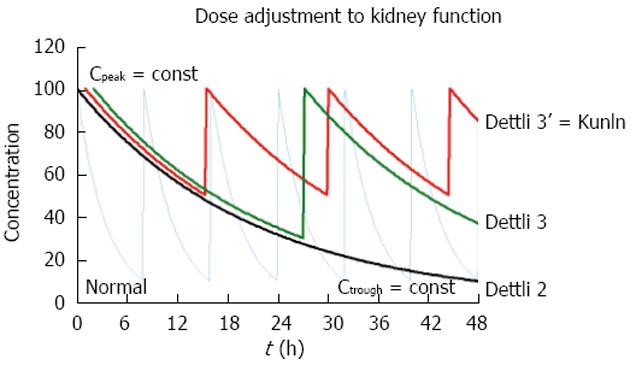
According to the proportional dose adjustment rules as proposed by Luzius Dettli, either the dose (D) should be reduced or the interval (Tau) extended (Figure 2). When the dose is reduced (Dettli 1) the peak levels are lower than in normal conditions but the trough levels are higher. When the administration interval is extended (Dettli 2) the peak and the trough concentrations are kept constant but the dosing frequency will decrease.
Math 16
The dosing alternative proposed by Calvin Kunin states: The loading dose is the normal dose (Dstart = Dnorm) and the maintenance dose is one half of the loading dose where the administration interval corresponds to one half-life[23]. The Kunin rule leads to normal peak levels but higher troughs, a larger area AUC and more frequent peaks than those obtained with the Dettli rule 2.
Math 17
The Kunin rule can be illustrated with the example of ampicillin. In kidney failure, the ampicillin dose is decreased from 2000 mg every 8 h to 1000 mg every 12 h, since the half-life increases from 1.0 to 13 h (Table 1). For a GFR of 30 mL/min, the ampicillin half-life can be estimated at 3.8 h, giving reason to extend the administration interval from 8 to 12 h but to not change the 2000 mg dose since the half-life is shorter than the administration interval.
A general dosing rule that combines the Kunin rule with the Dettli rule 2 has been mentioned by Luzius Dettli: the eliminated fraction rule (Dettli 3). With the Dettli rule 3, the administration interval is selected according to the target trough concentration while the peak is kept constant (Figure 3).
Math 18
For the condition where peak as well as trough concentrations are constant and maintained as in the normal situation, the Dettli rule 3 corresponds to the Dettli rule 2 with a proportional extension of the administration interval. For the condition where the peak is constant but the trough should be no less than one half of the peak, the Dettli 3 rule corresponds to the Kunin rule.
Which rule should be applied cannot be decided by pharmacokinetic principles alone, but pharmacodynamic principles must be considered too. In addition, whenever possible, therapeutic drug monitoring should be utilized. In times where tandem mass spectrometry LC-MS/MS is possible, nearly every drug could be measured.
Amikacin, gentamicin, tobramycin, teicoplanin and vancomycin, but recently also colistin, piperacillin, meropenem and linezolid are anti-infective drugs that routinely can be measured. When drug levels are measured for optimizing antimicrobial therapy, two important peculiarities must be observed. If impaired kidney function impacts pharmacokinetics, higher trough concentrations must be accepted to obtain efficient peak concentrations - this can be seen when the Dettli rule 1 or the Kunin rule are applied for dose adjustment (Figures 2 and 3). This was demonstrated by the use of aminoglycosides in HD patients where only troughs of at least 3 ng/mL are associated with peaks above 7 ng/mL and both peaks and troughs were significantly higher in those patients surviving than in those without anti-infective success[24,25].
In line with these statements, the target trough concentration for vancomycin has consistently been increased in the last 25 years. The area under the curve should be > 400 h x mg/L (= 24 h x Css; Css > 17 mg/L) to obtain an antimicrobial response with vancomycin[26]. The new targets are troughs of 15 ng/mL needed to guarantee peaks of 30 to 40 ng/mL[27]. The further increase in vancomycin dose and higher trough concentrations, however, might be associated with an increased risk of nephrotoxicity[28].
Counterintuitively, plasma binding does not have much impact on drug dosing since the absolute free drug concentration value (Cfree) is unchanged when bound concentrations change[29].
Cfree = C - Cbound = (C - ΔCbound) - (Cbound - ΔCbound) = const
If the binding decreases, only the total (Ctot) and the bound (Cbound) concentrations and not the free (Cfree) concentration will decrease. Since the effect is supposed to depend on free concentrations, lower total concentrations do not need a change in dosage. However, plasma binding does have an effect on drug monitoring as far as total concentrations are measured (Ctot = Cinitial - ΔCbound) and lower than normal concentrations must be the target when binding is less. This mainly applies to antibiotics with high plasma binding such as teicoplanin and ceftriaxone. And again, the decision as to which concentration should be the target can be made most rationally by considering pharmacodynamic criteria too.
Pharmacokinetics is a necessary requirement for drug dose adjustment, but only the combined use of pharmacokinetics and pharmacodynamics is the sufficient condition for drug dose adjustment. Although some drug action might follow the dynamics of an irreversible effect, the most general concept of pharmacodynamics is based on the sigmoid Hill equation describing reversible effects. Even after mechanistic analysis of bacterial growth and killing dynamics, the Hill equation applies also to modeling the antimicrobial effect[30,31]. The actual effect (E) is a function of the maximum effect and of the concentration producing the half-maximum effect (CE50). The Hill coefficient (H) gives a measure of the sigmoidicity of the effect concentration correlation.
Math 19
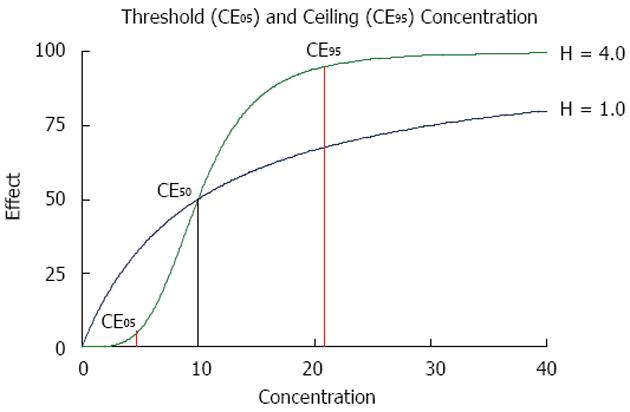
From the above equation, the threshold concentration (CE05) and the ceiling concentration (CE95) can be derived[32]. The threshold concentration produces only 5% of the maximum effect and the ceiling concentration produces 95% of the maximum effect. The higher the Hill coefficient, the higher the threshold concentration is, but the lower the ceiling concentration and the narrower the range of lower and upper target concentrations are (Figure 4).
Math 20
CE05 = CE50· 19-1/H
CE95 = CE50· 191/H
The ceiling concentration can be considered to be the upper limit of the target peak levels (Cpeak < CE95), whereas the threshold concentration marks the lower limit of effective trough levels (Ctrough > CE05). The distance between the ceiling and the threshold concentrations depends on H, not on CE50, and the ceiling-to-threshold time tceiling-threshold can be measured by multiples of the respective elimination half-life. For a drug with a short half-life and a high Hill coefficient, the therapeutic range of target concentrations can be very narrow (Figure 4).
This conclusion might be illustrated with the beta lactam antibiotic ceftazidime where the half-life is 2.1 h and short in patients with normal kidney function (Table 1) but the Hill coefficient is 3.7 and high[33]. These values yield a short peak to trough or ceiling-to-threshold time tceiling-threshold = 5 h, indicating that ceftazidime should be given at least every 6 h to maximize efficacy. In contrast, for gentamicin, the half-life is also 2 h (Table 1), but the Hill coefficient is 1.3 and low[33]. Thus, the estimated peak-to-trough time tceiling-threshold is longer than 13 h: Here the administration interval could be extended to 12 h or more (Tau = tceiling-threshold).
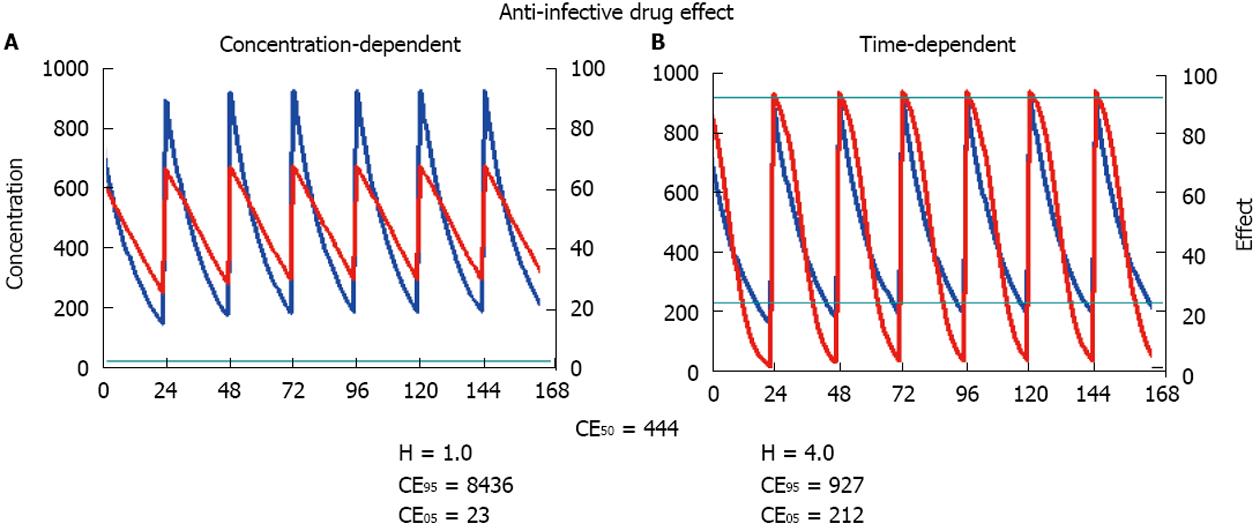
The clinical progress in anti-infective dosing that has had the greatest impact has probably been achieved with the differentiation of drugs with time-dependent from drugs with concentration-dependent action[34,35]. Specific examples are the penicillins, cephalosporins, vancomycin, teicoplanin, the penems and the antiviral drugs with a time-dependent effect whereas gentamicin, amikacin, daptomycin, colistin, ciprofloxacin or levofloxacin possess a concentration-dependent activity.
It has been shown that anti-infective drugs with a time-dependent effect have a significantly higher Hill coefficient than those with concentration-dependent action[33]. This difference translates into practical consequences for the threshold and the ceiling concentration. A high Hill coefficient is associated with a relatively low ceiling concentration but simultaneously with a high threshold concentration (Figure 4). Thus, the time interval should be short between dosing of time-dependent anti-infective drugs and it makes no sense to increase the dose above the ceiling concentration. In contrast, a low Hill coefficient is associated with a high ceiling concentration and a low threshold concentration. Thus, it might increase the effect of concentration-dependent anti-infective drugs to give a single high bolus dose but it is not so critical to extend the administration interval - as proposed for aminoglycosides[36]. On a practical level, it might prove optimal to administer anti-infective drugs with time-dependent action more frequently, or even as a continuous infusion[37,38]. By contrast, anti-infective drugs with concentration-dependent action should be given with a bolus and a high maintenance dose to increase efficacy (Figure 5).
The usual measures of the antimicrobial effect such as the time over minimal inhibitory concentration MIC, or the AUC over MIC, or the peak over MIC can be unified by the following concept: A close correlation of the MIC and the concentration producing the half-maximum effect can be predicted. However, it has been shown[33] that for concentration-dependent antimicrobial action, the minimal inhibitory concentration could fall considerably below the concentration producing the half-maximum effect (MIC << CE50). Consequently, it might be more reasonable to compare the bacteriological MIC with the pharmacodynamic parameter of a threshold concentration. Frequently the concentration target is stated as high as 4 times above the MIC. If this target corresponds to the CE50, this translates into an average sized Hill coefficient of H = 2.1 since the following condition might hold true.
Cthreshold = MIC = CE05 = CE50· 19-1/H
In agreement with this equation, the Hill coefficient of meropenem is reported at H = 3.1 for the MIC of 1.0 mg/L and a CE50 at 2.6 mg/L[33].
Potency is also a significant measure of microbiology. The potency is inversely proportional to the concentration CE50 producing the half maximum effect. Therefore, resistance of the strain is just another word for a change in the CE50 and thus for reduced potency of the drug.
potency = 1/CE50
To overcome resistance, a higher dose might be necessary since a high concentration CE50 is required to produce the half-maximum effect. This concept allows a distinction to be made between relative resistance and absolute drug resistance. A pathogen with relative resistance can be made sensitive by increasing the dose[39-41]. Thus, it has been recommended to treat severe infections with resistant strains by increasing the standard meropenem dose to 3 x 2000 mg per day[42,43] or the daptomycin dose to > 8 mg/kg per day[44] with careful monitoring of side effects.
From the concept of potency and the interpretation of the Hill coefficient, it can be considered plausible that the time-dependent action and the concentration-dependent action are only the extreme positions of a continuum. Every drug can be considered both concentration-dependent and time-dependent - more or less, either the one or the other[31]. The antimicrobial drug effect needs the presence of leukocytes, and less bacterial killing is reported in neutropenia[31]. Therefore, these patients need a 1.5 to 2 times higher than usual dose of anti-infective drugs[45]. In addition, the increasing rate of drug resistance in febrile neutropenia also strongly supports the concept of high dosing[31,46].
Anticancer drugs and anti-infective drugs should be used differently. The adjustment of anticancer drugs must not only be based on the kidney function but also on the physical condition of a patient. Tumor patients are older and anticancer drugs have a considerable potential for toxicity. Therefore, anticancer chemotherapy must be adjusted to both kidney function and to the general medical condition (in cases with Karnofsky index < 40% or ECOG > 2 performance status). In contrast to anticancer drugs, however, the anti-infective therapy should be adjusted to kidney function alone, but a compromised or even poor general condition should not result in a reduced dose or selection of less active anti-infective therapy. An immediate and sufficiently high antimicrobial therapy is needed in the most vulnerable, that is, in elderly and immunocompromised cancer patients. Where the risk is low, oral dosing of anti-infective drugs is sufficient in febrile neutropenia[47]. In most cases, however, intravenous dosing might be preferable with sequential oral dosing only in responders.
Ehrlich[48] stated the principle of anti-infective therapy: “frapper vite et frapper fort” meaning “hit fast, hit hard”.
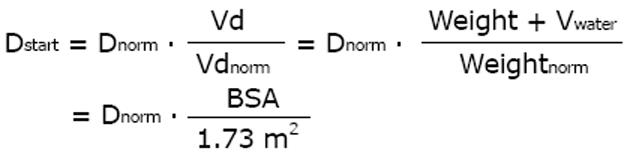
For anti-infective drug therapy, the immediate and high loading dose is very important[49,50]. According to the “Tarragona strategy” the antibiotic regimen should be started fast and with a loading dose, whereas the dose adjustment follows the course and clinical condition[51]. It can be a deleterious mistake to adjust the dose to the impaired kidney function but to give no loading dose (Figure 2). The loading dose is usually the normal standard dose. However, many patients in the intensive care unit are over-hydrated and the distribution volume is much larger than under normal conditions[34]. The loading dose could well be adjusted to such volume changes by applying the BSA.
Math 21
Thus, the required loading dose can be higher than the normal standard dose. In patients with sepsis, the gentamicin distribution volume was 0.35 L/kg vs 0.29 L/kg and significantly larger compared to intensive care patients without sepsis[52]. The need for a higher dose to initiate antimicrobial therapy can be stated as the rule when the immediate and high blood level is the target as with anti-infective therapy. The immediate start of treatment and an initially high concentration are also needed to avoid selection of resistant strains. Therefore, the antimicrobial treatment starts with a normal or even higher loading dose in the intensive care patients. Afterwards, the adjustment with a reduced maintenance dose is usually not needed before day 2 or 3 of anti-infective treatment[53].
A special problem occurs in the case of aminoglycosides: It is now standard practice to administer one single bolus dose per day instead of three divided doses[36]. Such a single high bolus dose will be associated with a 20-fold increase in the AUC if renal failure is present and the half-life increases from 2 to 40 h. For aminoglycosides, we propose administering only 50% of the standard high bolus loading dose to avoid excessive exposure in kidney failure or dialysis patients (Table 1). Following the loading dose, the maintenance dose can be estimated by one of the three Dettli rules, or the Kunin rule.
In addition to the case of over-hydration with an increase in distribution volume, the so-called augmented renal clearance has been brought into debate[54]. Augmented renal clearance is estimated from serum creatinine or endogenous creatinine clearance. If a patient is overhydrated, however, the serum creatinine is diluted, making creatinine clearance and creatinine-based GFR estimates falsely high. Since the clearance can be seen as the arithmetic product of elimination rate constant and distribution volume, the higher creatinine clearance in the patients with the systemic inflammatory response syndrome and sepsis could be explained by two mechanisms, augmented renal elimination and over-hydration. The consequences are different: augmented renal elimination needs a higher maintenance dose but over-hydration requires both an increase in the loading dose and a higher maintenance dose (= weight-based dosing as in pediatrics).
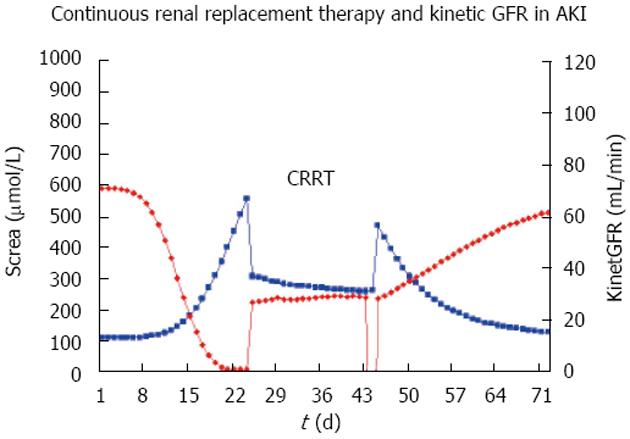
In the intensive care unit (ICU), three modalities are used as renal replacement therapy: Continuous hemofiltration (CRRT), sustained low efficiency daily dialysis (SLEDD) and intermittent HD. The hemofiltration is applied with variable modifications either of the surface area, of the filter membrane, with predilution or post-dilution replacement fluid, and variable ultrafiltration rates that are used along with the corresponding flow rate of the substitution volume. Therefore, a global measure of the effect of hemofiltration on drug elimination will be very useful and the total creatinine clearance or the other creatinine-based measures of the GFR have been proposed for this purpose[9,55,56]. The recently introduced kinetic GFR applies also to patients with CRRT[14], and thus has clear advantages in the intensive care unit where the medical conditions can change rapidly (Figure 6).
totalCLcrea = Filtrationkedney + FiltrationCRRT
totalCLcrea = eGFR = MDRDGFR = CKD - EPIGFR = C and GGFR
totalCLcrea = kinetGFR
There is a trend to underestimate drug elimination by CRRT and consequently under-dose antimicrobials in the ICU[57]. By using the total creatinine clearance, the creatinine-based GFR estimates or the kinetic GFR, the dose can be adjusted according to the rules of Dettli and Kunin also for patients on CRRT. As a rule and to avoid under-dosage, the normal standard dosage should be given and not be reduced if the total creatinine clearance is above 60 mL/min.
A combination of continuous and intermittent renal replacement is the SLEDD. The frequency of under-dosage is estimated with a median value of 70% whereas the risk of over-dosage was only 5% while on SLEDD[6,58]. If this kind of treatment is applied, the daily dose at least corresponds to the post HD dose (see below) but recommendations vary widely.
DSLEDD = DHD ≈ Dstart
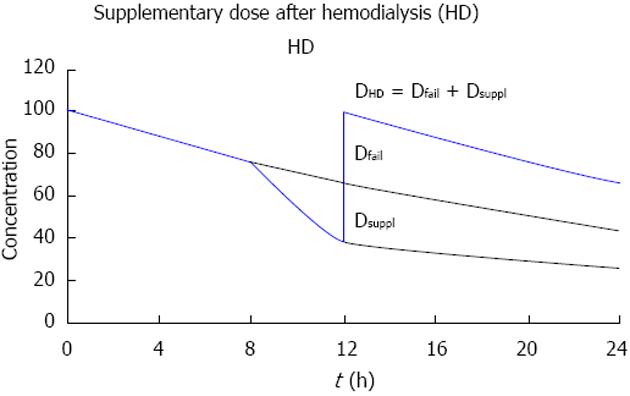
More complex is the drug dosing when intermittent HD is performed (Figure 7). Off dialysis, the dose must be adjusted to the failing kidney function. For intermittent HD, we argue that it is better to give the dose not at the beginning but at the end or immediately after HD. With a pre-dialysis dose, no anti-infective effect will be maintained in the interval off dialysis[59].
If the drug is given after dialysis, the post-dialysis dose should replace first the amount eliminated during the interval off dialysis, that is, the dose for failing kidney function (Dfail). In addition to that, the effect of HD should be compensated by a supplementary dose (Dsuppl) replacing the fraction eliminated on dialysis (FR).
DHD = Dfail + Dsuppl
Dsuppl = FR · (Dstart - Dfail)
FR = 1 - exp [(- 0.693/T1/2on) · ton]
Thus, the dose after HD is higher than the adjusted maintenance dose[9]. In many cases the dose after HD is another loading dose (Dstart). The post-dialysis dose (DHD) can again be illustrated with the example of ampicillin: The fraction eliminated by dialysis is implicitly stated in NEPharm (40%) and the dose after dialysis is 2000 mg corresponding to the size of the normal loading dose (Table 1).
DHD ≈ Dstart
In contrast to the usual post-dialysis dosing, it might be a good option to perform HD after drug administration for removal of high-dose anticancer therapy administered before dialysis. In analogy, the dosing immediately before dialysis has been also proposed for aminoglycosides[60]. With a pre-dialysis regimen, however, aminoglycosides must be given at a higher dose (gentamicin up to 400 mg) and HD should be performed on a daily basis in order to not miss the antimicrobial effect in the interval off dialysis.
The prevalence of CKD and incidence of AKI are high in patients with malignancies. This generally makes dose adjustment necessary, usually ending in a lower dose than normal. Since 1978, we have documented pharmacokinetic parameters in the NEPharm database from extracted PubMed citations[61-63]. With the parameters recorded in NEPharm and based on the above pharmacokinetic/pharmacodynamic considerations, we have made explicit dose proposals. These recommendations are used in our institution and subjected to continuous updates (Table 1).
Anti-infective therapy should start immediately without any delay and with a high dose. Dose adjustment follows on day 2 or later in the course of treatment[53]. A loading dose that takes into account the real volume especially in volume-expanded patients should be given. When in doubt, we propose that the peak level should be the target and the standard dose should be given with an extended administration interval when kidney function is impaired[9].
The anti-infective therapy should be optimized by therapeutic drug monitoring whenever possible (gentamicin, tobramycin, amikacin, vancomycin, teicoplanin, colistin, piperacillin, meropenem, linezolid). However, the adequate practical consequences should be drawn from the measured concentrations. In patients with impaired kidney function, higher trough concentrations result from the dose adjustment according to Dettli 1, Dettli 3 or Kunin. Only the Dettli rule 2 is associated with the same peak and trough concentrations as under normal conditions. On the other hand, the plasma binding of many drugs can decrease in kidney dysfunction. In this case, lower trough concentrations are acceptable (ceftriaxone, teicoplanin) since the absolute free concentration does not change when the bound fraction decreases but free concentrations produce the effect.
The modern distinction between time-dependent and concentration-dependent effects can be parameterized by the Hill coefficient. A high Hill coefficient (> 2.1) indicates time-dependent drug action, whereas a low Hill coefficient (< 2.1) indicates concentration-dependent action. Based on the Hill equation, the threshold concentration can be distinguished from the ceiling concentration. A high Hill coefficient determines that the ceiling concentration is low but the threshold concentration is relatively high (Figure 4). In contrast, a low Hill coefficient determines that the ceiling concentration is relatively high but the threshold concentration is low. We suggest that the minimal inhibitory concentration from microbiology be correlated to the threshold concentration. The target concentration should not be less than the threshold concentration for time-dependent effects, but the target concentration could be as high as the ceiling concentration for concentration-dependent effects.
To decide between the pharmacokinetic dosing alternatives (Dettli 1-3), pharmacodynamic considerations can give an answer to whether the dose should be reduced or the interval extended in kidney dysfunction: (1) For time-dependent anti-infective action, more frequent dosing is more effective than maintaining the single high dose[35]: The target trough levels should be kept above the threshold concentration (Figure 5). The beta lactam antibiotics oxacillin or piperacillin are considered to exhibit a time-dependent action. Accordingly, it has been shown that continuous infusion produces a better antimicrobial response than intermittent dosing of the respective daily dose[37,38]; and (2) For concentration-dependent anti-infective action, however, the extension of the interval is less disadvantageous than reducing the single dose (Figure 5). The target peak levels should be close to the ceiling concentration and kept as high as possible[35]. The quinolone ciprofloxacin exhibits concentration-dependent action. Here, the high bolus dosing produced a more rapid bactericidal effect than the more frequent application of a lower dose[33,64]. Also for aminoglycosides, a high peak concentration is superior to more frequent dosing to induce bacterial killing[36,65].
For drugs with a high Hill coefficient, the area under the effect time curve may fall disproportionally less and result insufficient with a lower dose[61]. Therefore, we discourage proportional dose reduction, especially Dettli 1, if the Hill coefficient is unknown. The risk of selecting resistant strains is also less when the initial dose is high[31].
The time above MIC reflects effect duration. A pharmacodynamic measure for the duration of drug effect, the time of effect duration (TED), can be derived from the elimination half-life[18]. The intuitively most evident effect duration time is the effect bisection time (TED50) that is correlated to the elimination half-life (T1/2), the peak concentration (Cpeak) and the Hill coefficient (H) along with the concentration (CE50) producing the half-maximum effect[18].
Math 22
The longer the half-life and the higher the peak concentration - but the less the CE50 - the longer lasting the effect is. The half-life is 1.0 h (Table 1) and the Hill coefficient is stated at H = 3.1 for meropenem[33]. If the MIC of 6 mg/l[44] is equated to the threshold concentration (CE05 = MIC), the CE50 can be estimated at 37 mg/L. With a dose of 500 mg every 8 h and a peak concentration of 50 mg/L[44], the effect bisection time will be estimated at TED50 = 0.71 h. Doubling the dose, however, will more than double the effect bisection time TED50 to 1.5 h, thus extending the drug action while the pharmacokinetic half-life of 1.0 h is the same. However, the standard dose administered more frequently would not increase the effect bisection time.
The dose in patients with continuous renal replacement therapy can be derived from the creatinine-based GFR estimates or in case of changing kidney function, from the “kinetic GFR” (Figure 6). If this GFR estimate is above 60 mL/min, no dose adjustment is required. For intermittent HD a supplementary dose should be given after dialysis (Figure 7). The supplementary dose adds with the dose adjusted to renal failure to the post-HD dose that can be as high as the loading dose. This practice might be prudent also in cases where the drug fraction eliminated during HD is not known.
P- Reviewer: Bellomo G, Friedman EA, Mahmoud KM, Yong D S- Editor: Tian YL L- Editor: A E- Editor: Yan JL
| 1. | Nomura K, Ishida Y. [Optimal administration of antimicrobial agents for febrile neutropenia in patients with hematological malignancies]. Nihon Rinsho. 2010;68:1403-1411. [PubMed] |
| 2. | Perazella MA. Onco-nephrology: renal toxicities of chemotherapeutic agents. Clin J Am Soc Nephrol. 2012;7:1713-1721. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 188] [Cited by in RCA: 194] [Article Influence: 14.9] [Reference Citation Analysis (1)] |
| 3. | Lowrance WT, Ordoñez J, Udaltsova N, Russo P, Go AS. CKD and the risk of incident cancer. J Am Soc Nephrol. 2014;25:2327-2334. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 140] [Cited by in RCA: 200] [Article Influence: 18.2] [Reference Citation Analysis (1)] |
| 4. | Launay-Vacher V. Epidemiology of chronic kidney disease in cancer patients: lessons from the IRMA study group. Semin Nephrol. 2010;30:548-556. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 63] [Cited by in RCA: 67] [Article Influence: 4.5] [Reference Citation Analysis (0)] |
| 5. | Janus N, Launay-Vacher V, Byloos E, Machiels JP, Duck L, Kerger J, Wynendaele W, Canon JL, Lybaert W, Nortier J. Cancer and renal insufficiency results of the BIRMA study. Br J Cancer. 2010;103:1815-1821. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 116] [Cited by in RCA: 134] [Article Influence: 8.9] [Reference Citation Analysis (0)] |
| 6. | Harris LE, Reaves AB, Krauss AG, Griner J, Hudson JQ. Evaluation of antibiotic prescribing patterns in patients receiving sustained low-efficiency dialysis: opportunities for pharmacists. Int J Pharm Pract. 2013;21:55-61. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 21] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 7. | Walser M. Assessing renal function from creatinine measurements in adults with chronic renal failure. Am J Kidney Dis. 1998;32:23-31. [PubMed] |
| 8. | Matsushita K, Mahmoodi BK, Woodward M, Emberson JR, Jafar TH, Jee SH, Polkinghorne KR, Shankar A, Smith DH, Tonelli M. Comparison of risk prediction using the CKD-EPI equation and the MDRD study equation for estimated glomerular filtration rate. JAMA. 2012;307:1941-1951. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 728] [Cited by in RCA: 745] [Article Influence: 57.3] [Reference Citation Analysis (0)] |
| 9. | Matzke GR, Aronoff GR, Atkinson AJ, Bennett WM, Decker BS, Eckardt KU, Golper T, Grabe DW, Kasiske B, Keller F. Drug dosing consideration in patients with acute and chronic kidney disease-a clinical update from Kidney Disease: Improving Global Outcomes (KDIGO). Kidney Int. 2011;80:1122-1137. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 279] [Cited by in RCA: 307] [Article Influence: 21.9] [Reference Citation Analysis (0)] |
| 10. | Mosteller RD. Simplified calculation of body-surface area. N Engl J Med. 1987;317:1098. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1521] [Cited by in RCA: 2016] [Article Influence: 53.1] [Reference Citation Analysis (0)] |
| 11. | Park EJ, Wu K, Mi Z, Dong T, Lawrence JP, Ko CW, Huang SM, Zhang L, Crentsil V, Zhang J. A systematic comparison of cockcroft-gault and modification of diet in renal disease equations for classification of kidney dysfunction and dosage adjustment. Ann Pharmacother. 2012;46:1174-1187. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 41] [Cited by in RCA: 42] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 12. | Keller F, Hartmann B. An easy to calculate equation to estimate GFR based on inulin clearance. Nephrol Dial Transplant. 2010;25:1345-1346; author reply 1346-1347. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 13. | Tsinalis D, Thiel GT. An easy to calculate equation to estimate GFR based on inulin clearance. Nephrol Dial Transplant. 2009;24:3055-3061. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 8] [Cited by in RCA: 10] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 14. | Chen S. Retooling the creatinine clearance equation to estimate kinetic GFR when the plasma creatinine is changing acutely. J Am Soc Nephrol. 2013;24:877-888. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 131] [Cited by in RCA: 147] [Article Influence: 12.3] [Reference Citation Analysis (0)] |
| 15. | Benet LZ. Clearance (née Rowland) concepts: a downdate and an update. J Pharmacokinet Pharmacodyn. 2010;37:529-539. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 22] [Cited by in RCA: 19] [Article Influence: 1.3] [Reference Citation Analysis (0)] |
| 16. | Dost FH. [Half value time and total clearance]. Z Gesamte Inn Med. 1954;9:546-551. [PubMed] |
| 17. | Schiffer JT, Swan DA, Corey L, Wald A. Rapid viral expansion and short drug half-life explain the incomplete effectiveness of current herpes simplex virus 2-directed antiviral agents. Antimicrob Agents Chemother. 2013;57:5820-5829. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 40] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 18. | Keller F, Hartmann B, Czock D. Time of effect duration and administration interval for sitagliptin in patients with kidney failure. Eur J Drug Metab Pharmacokinet. 2014;39:77-85. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2] [Cited by in RCA: 3] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 19. | Kunin CM, Rees SB, Merrill JP, Finland M. Persistence of antibiotics in blood of patients with acute renal failure. I. Tetracycline and chlortetracycline. J Clin Invest. 1959;38:1487-1497. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 64] [Cited by in RCA: 72] [Article Influence: 2.7] [Reference Citation Analysis (0)] |
| 20. | Dettli LC. Drug dosage in patients with renal disease. Clin Pharmacol Ther. 1974;16:274-280. [PubMed] |
| 21. | Giusti DL, Hayton WL. Dosage regimen adjustments in renal impairment. Drug Intell Clin Pharm. 1973;7:382-387. |
| 22. | Yeung CK, Shen DD, Thummel KE, Himmelfarb J. Effects of chronic kidney disease and uremia on hepatic drug metabolism and transport. Kidney Int. 2014;85:522-528. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 132] [Cited by in RCA: 157] [Article Influence: 13.1] [Reference Citation Analysis (0)] |
| 23. | Kunin CM. A guide to use of antibiotics in patients with renal disease. A table of recommended doses and factors governing serum levels. Ann Intern Med. 1967;67:151-158. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 141] [Cited by in RCA: 99] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 24. | Keller F, Wagner K, Borner K, Kemmerich B, Lode H, Offermann G, Distler A. Aminoglycoside dosage in hemodialysis patients. J Clin Pharmacol. 1986;26:690-695. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 7] [Cited by in RCA: 8] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 25. | Keller F, Borner K, Schwarz A, Offermann G, Lode H. Therapeutic aminoglycoside monitoring in renal failure patients. Ther Drug Monit. 1987;9:148-153. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 17] [Cited by in RCA: 19] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 26. | Moise-Broder PA, Forrest A, Birmingham MC, Schentag JJ. Pharmacodynamics of vancomycin and other antimicrobials in patients with Staphylococcus aureus lower respiratory tract infections. Clin Pharmacokinet. 2004;43:925-942. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 618] [Cited by in RCA: 576] [Article Influence: 27.4] [Reference Citation Analysis (0)] |
| 27. | Davis SL, Scheetz MH, Bosso JA, Goff DA, Rybak MJ. Adherence to the 2009 consensus guidelines for vancomycin dosing and monitoring practices: a cross-sectional survey of U.S. hospitals. Pharmacotherapy. 2013;33:1256-1263. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 46] [Cited by in RCA: 49] [Article Influence: 4.1] [Reference Citation Analysis (0)] |
| 28. | Lodise TP, Patel N, Lomaestro BM, Rodvold KA, Drusano GL. Relationship between initial vancomycin concentration-time profile and nephrotoxicity among hospitalized patients. Clin Infect Dis. 2009;49:507-514. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 414] [Cited by in RCA: 435] [Article Influence: 27.2] [Reference Citation Analysis (0)] |
| 29. | Benet LZ, Hoener BA. Changes in plasma protein binding have little clinical relevance. Clin Pharmacol Ther. 2002;71:115-121. [PubMed] |
| 30. | Czock D, Markert C, Hartman B, Keller F. Pharmacokinetics and pharmacodynamics of antimicrobial drugs. Expert Opin Drug Metab Toxicol. 2009;5:475-487. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 25] [Cited by in RCA: 25] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 31. | Ankomah P, Levin BR. Exploring the collaboration between antibiotics and the immune response in the treatment of acute, self-limiting infections. Proc Natl Acad Sci USA. 2014;111:8331-8338. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 81] [Cited by in RCA: 99] [Article Influence: 9.0] [Reference Citation Analysis (0)] |
| 32. | Hartmann B, Czock D, Keller F. Drug therapy in patients with chronic renal failure. Dtsch Arztebl Int. 2010;107:647-655; quiz 655-656. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 31] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 33. | Czock D, Keller F. Mechanism-based pharmacokinetic-pharmacodynamic modeling of antimicrobial drug effects. J Pharmacokinet Pharmacodyn. 2007;34:727-751. [PubMed] |
| 34. | Eyler RF, Mueller BA. Antibiotic dosing in critically ill patients with acute kidney injury. Nat Rev Nephrol. 2011;7:226-235. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 70] [Cited by in RCA: 68] [Article Influence: 4.9] [Reference Citation Analysis (0)] |
| 35. | Eyler RF, Mueller BA. Antibiotic pharmacokinetic and pharmacodynamic considerations in patients with kidney disease. Adv Chronic Kidney Dis. 2010;17:392-403. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 27] [Cited by in RCA: 22] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 36. | Kashuba AD, Nafziger AN, Drusano GL, Bertino JS. Optimizing aminoglycoside therapy for nosocomial pneumonia caused by gram-negative bacteria. Antimicrob Agents Chemother. 1999;43:623-629. [PubMed] |
| 37. | Hughes DW, Frei CR, Maxwell PR, Green K, Patterson JE, Crawford GE, Lewis JS. Continuous versus intermittent infusion of oxacillin for treatment of infective endocarditis caused by methicillin-susceptible Staphylococcus aureus. Antimicrob Agents Chemother. 2009;53:2014-2019. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 37] [Cited by in RCA: 39] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 38. | Lorente L, Jiménez A, Martín MM, Iribarren JL, Jiménez JJ, Mora ML. Clinical cure of ventilator-associated pneumonia treated with piperacillin/tazobactam administered by continuous or intermittent infusion. Int J Antimicrob Agents. 2009;33:464-468. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 85] [Cited by in RCA: 90] [Article Influence: 5.6] [Reference Citation Analysis (0)] |
| 39. | Gracia-Ahufinger I, Gutiérrez-Aroca J, Cordero E, Vidal E, Cantisán S, del Castillo D, Martín-Gandul C, Rivero A, Torre-Cisneros J. Use of high-dose ganciclovir for the treatment of cytomegalovirus replication in solid organ transplant patients with ganciclovir resistance-inducing mutations. Transplantation. 2013;95:1015-1020. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 35] [Cited by in RCA: 39] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 40. | Llor C, Arranz J, Morros R, García-Sangenís A, Pera H, Llobera J, Guillén-Solà M, Carandell E, Ortega J, Hernández S. Efficacy of high doses of oral penicillin versus amoxicillin in the treatment of adults with non-severe pneumonia attended in the community: study protocol for a randomised controlled trial. BMC Fam Pract. 2013;14:50. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 2] [Cited by in RCA: 3] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 41. | Gould IM, Miró JM, Rybak MJ. Daptomycin: the role of high-dose and combination therapy for Gram-positive infections. Int J Antimicrob Agents. 2013;42:202-210. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 71] [Article Influence: 5.9] [Reference Citation Analysis (0)] |
| 42. | Kiratisin P, Keel RA, Nicolau DP. Pharmacodynamic profiling of doripenem, imipenem and meropenem against prevalent Gram-negative organisms in the Asia-Pacific region. Int J Antimicrob Agents. 2013;41:47-51. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 10] [Cited by in RCA: 11] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 43. | Binder L, Schwörer H, Hoppe S, Streit F, Neumann S, Beckmann A, Wachter R, Oellerich M, Walson PD. Pharmacokinetics of meropenem in critically ill patients with severe infections. Ther Drug Monit. 2013;35:63-70. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 38] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 44. | Kullar R, Casapao AM, Davis SL, Levine DP, Zhao JJ, Crank CW, Segreti J, Sakoulas G, Cosgrove SE, Rybak MJ. A multicentre evaluation of the effectiveness and safety of high-dose daptomycin for the treatment of infective endocarditis. J Antimicrob Chemother. 2013;68:2921-2926. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 71] [Cited by in RCA: 77] [Article Influence: 6.4] [Reference Citation Analysis (0)] |
| 45. | Drusano GL, Louie A, Deziel M, Gumbo T. The crisis of resistance: identifying drug exposures to suppress amplification of resistant mutant subpopulations. Clin Infect Dis. 2006;42:525-532. [PubMed] |
| 46. | Goulenok T, Fantin B. Antimicrobial treatment of febrile neutropenia: pharmacokinetic-pharmacodynamic considerations. Clin Pharmacokinet. 2013;52:869-883. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 9] [Cited by in RCA: 15] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 47. | Kern WV, Marchetti O, Drgona L, Akan H, Aoun M, Akova M, de Bock R, Paesmans M, Viscoli C, Calandra T. Oral antibiotics for fever in low-risk neutropenic patients with cancer: a double-blind, randomized, multicenter trial comparing single daily moxifloxacin with twice daily ciprofloxacin plus amoxicillin/clavulanic acid combination therapy--EORTC infectious diseases group trial XV. J Clin Oncol. 2013;31:1149-1156. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 56] [Cited by in RCA: 62] [Article Influence: 5.2] [Reference Citation Analysis (0)] |
| 48. | Ehrlich P. Chemotherapeutics: scientific principles, methods and results. Lancet. 1913;2:353-359. |
| 49. | Harbarth S, Garbino J, Pugin J, Romand JA, Lew D, Pittet D. Inappropriate initial antimicrobial therapy and its effect on survival in a clinical trial of immunomodulating therapy for severe sepsis. Am J Med. 2003;115:529-535. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 454] [Cited by in RCA: 451] [Article Influence: 20.5] [Reference Citation Analysis (0)] |
| 50. | Kumar A, Ellis P, Arabi Y, Roberts D, Light B, Parrillo JE, Dodek P, Wood G, Kumar A, Simon D. Initiation of inappropriate antimicrobial therapy results in a fivefold reduction of survival in human septic shock. Chest. 2009;136:1237-1248. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 744] [Cited by in RCA: 812] [Article Influence: 50.8] [Reference Citation Analysis (0)] |
| 51. | Sandiumenge A, Diaz E, Bodí M, Rello J. Therapy of ventilator-associated pneumonia. A patient-based approach based on the ten rules of “The Tarragona Strategy”. Intensive Care Med. 2003;29:876-883. [PubMed] |
| 52. | Buijk SE, Mouton JW, Gyssens IC, Verbrugh HA, Bruining HA. Experience with a once-daily dosing program of aminoglycosides in critically ill patients. Intensive Care Med. 2002;28:936-942. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 122] [Cited by in RCA: 112] [Article Influence: 4.9] [Reference Citation Analysis (0)] |
| 53. | Ulldemolins M, Vaquer S, Llauradó-Serra M, Pontes C, Calvo G, Soy D, Martín-Loeches I. Beta-lactam dosing in critically ill patients with septic shock and continuous renal replacement therapy. Crit Care. 2014;18:227. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 57] [Cited by in RCA: 65] [Article Influence: 5.9] [Reference Citation Analysis (0)] |
| 54. | Claus BO, Hoste EA, Colpaert K, Robays H, Decruyenaere J, De Waele JJ. Augmented renal clearance is a common finding with worse clinical outcome in critically ill patients receiving antimicrobial therapy. J Crit Care. 2013;28:695-700. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 144] [Cited by in RCA: 164] [Article Influence: 13.7] [Reference Citation Analysis (0)] |
| 55. | Keller F, Böhler J, Czock D, Zellner D, Mertz AK. Individualized drug dosage in patients treated with continuous hemofiltration. Kidney Int Suppl. 1999;S29-S31. [PubMed] |
| 56. | Bouman CS. Antimicrobial dosing strategies in critically ill patients with acute kidney injury and high-dose continuous veno-venous hemofiltration. Curr Opin Crit Care. 2008;14:654-659. [PubMed] |
| 57. | Seyler L, Cotton F, Taccone FS, De Backer D, Macours P, Vincent JL, Jacobs F. Recommended β-lactam regimens are inadequate in septic patients treated with continuous renal replacement therapy. Crit Care. 2011;15:R137. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 162] [Cited by in RCA: 179] [Article Influence: 12.8] [Reference Citation Analysis (0)] |
| 58. | Bogard KN, Peterson NT, Plumb TJ, Erwin MW, Fuller PD, Olsen KM. Antibiotic dosing during sustained low-efficiency dialysis: special considerations in adult critically ill patients. Crit Care Med. 2011;39:560-570. [PubMed] |
| 59. | Janus N, Thariat J, Boulanger H, Deray G, Launay-Vacher V. Proposal for dosage adjustment and timing of chemotherapy in hemodialyzed patients. Ann Oncol. 2010;21:1395-1403. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 119] [Cited by in RCA: 118] [Article Influence: 7.9] [Reference Citation Analysis (0)] |
| 60. | Veinstein A, Venisse N, Badin J, Pinsard M, Robert R, Dupuis A. Gentamicin in hemodialyzed critical care patients: early dialysis after administration of a high dose should be considered. Antimicrob Agents Chemother. 2013;57:977-982. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 21] [Cited by in RCA: 24] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 61. | Aymanns C, Keller F, Maus S, Hartmann B, Czock D. Review on pharmacokinetics and pharmacodynamics and the aging kidney. Clin J Am Soc Nephrol. 2010;5:314-327. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 102] [Cited by in RCA: 88] [Article Influence: 5.9] [Reference Citation Analysis (0)] |
| 62. | Zellner D, Schromm T, Frankewitsch T, Giehl M, Keller F. Structured data entry for reliable acquisition of pharmacokinetic data. Methods Inf Med. 1996;35:261-264. [PubMed] |
| 63. | Keller F, Frankewitsch T, Zellner D, Simon S, Czock D, Giehl M. Standardized structure and modular design of a pharmacokinetic database. Comput Methods Programs Biomed. 1998;55:107-115. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 9] [Cited by in RCA: 8] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 64. | Czock D, Rasche FM. Dose adjustment of ciprofloxacin in renal failure: reduce the dose or prolong the administration interval. Eur J Med Res. 2005;10:145-148. [PubMed] |
| 65. | Moore RD, Lietman PS, Smith CR. Clinical response to aminoglycoside therapy: importance of the ratio of peak concentration to minimal inhibitory concentration. J Infect Dis. 1987;155:93-99. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 834] [Cited by in RCA: 819] [Article Influence: 21.6] [Reference Citation Analysis (0)] |