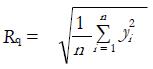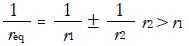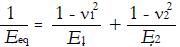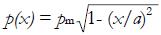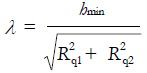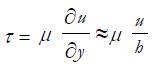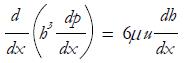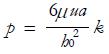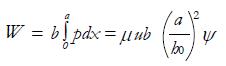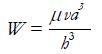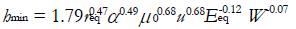Peer-review started: December 29, 2013
First decision: February 13, 2014
Revised: March 25, 2014
Accepted: May 14, 2014
Article in press: May 14, 2014
Published online: January 18, 2015
Processing time: 387 Days and 17.3 Hours
Hip arthroplasty can be considered one of the major successes of orthopedic surgery, with more than 350000 replacements performed every year in the United States with a constantly increasing rate. The main limitations to the lifespan of these devices are due to tribological aspects, in particular the wear of mating surfaces, which implies a loss of matter and modification of surface geometry. However, wear is a complex phenomenon, also involving lubrication and friction. The present paper deals with the tribological performance of hip implants and is organized in to three main sections. Firstly, the basic elements of tribology are presented, from contact mechanics of ball-in-socket joints to ultra high molecular weight polyethylene wear laws. Some fundamental equations are also reported, with the aim of providing the reader with some simple tools for tribological investigations. In the second section, the focus moves to artificial hip joints, defining materials and geometrical properties and discussing their friction, lubrication and wear characteristics. In particular, the features of different couplings, from metal-on-plastic to metal-on-metal and ceramic-on-ceramic, are discussed as well as the role of the head radius and clearance. How friction, lubrication and wear are interconnected and most of all how they are specific for each loading and kinematic condition is highlighted. Thus, the significant differences in patients and their lifestyles account for the high dispersion of clinical data. Furthermore, such consideration has raised a new discussion on the most suitable in vitro tests for hip implants as simplified gait cycles can be too far from effective implant working conditions. In the third section, the trends of hip implants in the years from 2003 to 2012 provided by the National Joint Registry of England, Wales and Northern Ireland are summarized and commented on in a discussion.
Core tip: In this paper, the biotribology of hip implants is described at different levels, from the more general definitions of friction, lubrication and wear and from some basic equations, to clinical data of different implants. The topic is presented both qualitatively and quantitatively, which we believe is an original approach for a review of this kind. Some simple mathematical tools are provided, which can also be useful for non-specialists to better understand the matter and to deal with simple tribological problems. Finally, the trends of artificial hip joints over the last ten years are discussed on the basis of tribological concepts.
- Citation: Puccio FD, Mattei L. Biotribology of artificial hip joints. World J Orthop 2015; 6(1): 77-94
- URL: https://www.wjgnet.com/2218-5836/full/v6/i1/77.htm
- DOI: https://dx.doi.org/10.5312/wjo.v6.i1.77
Although tribological phenomena are widespread in everyday life, the word tribology sounds new and strange to most people. Thus, it is usual, before speaking of tribology to non-tribologists, to introduce its literal meaning. The term tribology comes from the Greek words tribos = rubbing/friction and logos = science, so it is defined as the science of rubbing surfaces. In other words, it is known as the science of interacting surfaces in relative motion and encompasses many concepts, such as friction, wear and lubrication[1]. Therefore, tribology is in the tyre rolling over the road, in the head-disk interface of a hard disk driver, in the blinking of the eye, and so on.
When interacting surfaces belong to the human body or animals, including artificial joints, the term biotribology is usually preferred. The importance of the tribological performance of an artificial hip joint is well known in clinical practice. In fact, although hip arthroplasty is considered one of the major successes of orthopedic surgery, wear still remains a critical issue that limits the implant lifespan to 10-15 years. The incidence of hip arthroplasties is proved by the increasing rate of procedures per year, about 332000 in 2010 in the United States[2] and 76500 in 2012 in the United Kingdom (+ 7% compared to 2011)[3]. Additionally, according to the United Kingdom National Report 2013[3], 10000 revision surgeries were performed, with a 12% increment that can be attributed to the younger and more active patients who were treated with this procedure.
This paper describes the tribological features of hip implants with the aim of providing some key concepts for analyzing and improving current designs and maybe suggesting new solutions. A background on the main concepts of tribology is premised. Finally, the trend of hip arthroplasty over the last ten years is discussed.
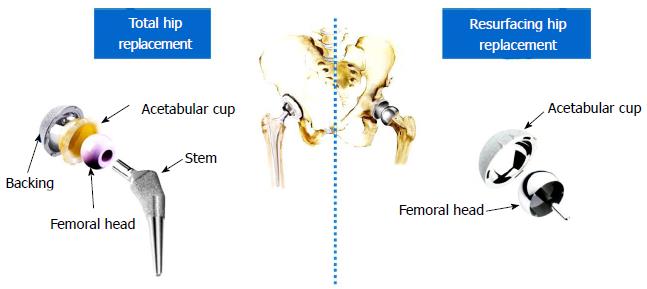
Nowadays, the world market has several hundred different brands of hip replacements, among which the surgeon will select one on the basis of patient symptoms and characteristics (e.g., gender, age) and her/his own clinical experience. This huge number of hip replacements can be classified according to their geometry (structure and dimensions) and materials. The structure of a total hip replacement (THR) and resurfacing hip replacement (RHR) can be compared (Figure 1).
The former is made up of a stem, a femoral head, an acetabular cup combined with, if cementless, a metallic shell which helps bone grow into it. RHR covers the articulating surfaces with a traditional cup and a head liner, thus preserving more bone. Both types of implants are available in several sizes but, in general, RHRs are characterized by bigger heads which should improve the implant stability.
The most commonly used materials for implant components are plastic (P), metal (M) and ceramic (C). The plastic is used only for the socket, whilst the others are used for both head and cup. The most common material combinations for the bearing surfaces are: metal-on-plastic (MoP), ceramic-on-plastic (CoP), ceramic-on-ceramic (CoC) and metal-on-metal (MoM) (Figure 2). In these acronyms, the first letter refers to the cup material and the third to the head. It is worth noting that RHRs are available only in MoM (MoMRHR) or CoM combinations. As the materials strongly influence the device tribological behavior, some further details on their properties will be discussed in Sec. 4.2.
In this section, the basic aspects of tribological phenomena are summarized in order to provide the main concepts for understanding the behavior and design of implants. More detailed explanations can be found in tribology textbooks as in[4,5].
Let us consider two interacting surfaces in relative motion. Phenomena that occur between them can be considered at macro or micro scale and are mainly dependent on the loading and kinematic (motion) conditions, as well as the presence of a lubricant.
Geometrical characteristics: When dealing with the geometrical characteristics of interacting bodies, a first distinction is made between conformal and non-conformal surfaces; in the first case, surfaces fit together geometrically so that the contact involves a wide area, while the opposite happens in the second case.
From a mechanical point of view, the natural/artificial hip is considered a conformal spherical or ball-in-socket joint, where the head and the cup have the same nominal radius. For practical manufacturing but also tribological reasons, a small clearance between the elements, usually in the order of tenth of microns, is properly defined. The higher the clearance, the less conformal the surfaces.
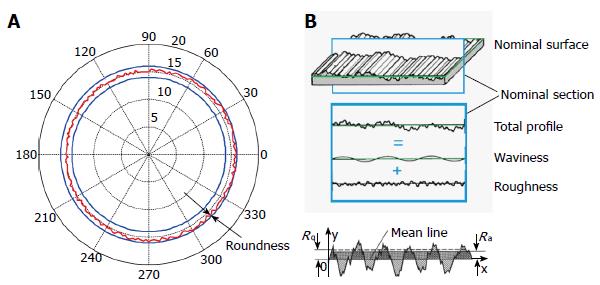
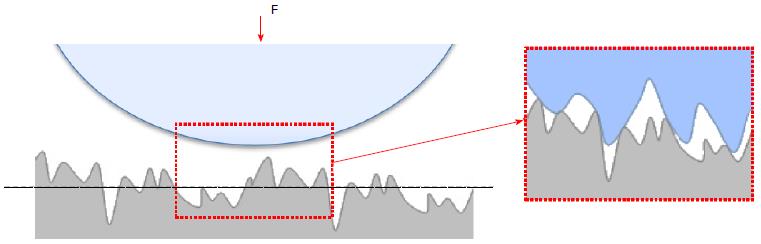
The nominal contact surfaces of the cup and head are portions of spheres. However, real surfaces (even in the initial unworn conditions) can have some deviations from the nominal shape, which are usually described in terms of roundness, waviness and roughness (Figure 3). The roundness (Figure 3A) defines the maximum radial distance between two concentric spheres that limits the real surface of the cup/head; it is associated with the manufacturing process and is usually in the order of a few microns.
In Figure 3B, a scheme of the nominal and real surfaces is reported, showing the meaning of waviness and roughness as deviations from the nominal profile, the former on a wider wavelength than the latter. It can be observed that roughness refers to the micro scale (finely spaced) irregularities of the real/measured surface, which can be described by means of several parameters, such as the average roughness Ra and the root mean squared roughness Rq, defined as
Math 24
and
Math 25
(1)
where i = 1..n is the number of points where heights yi were measured (Figure 3B).
The surface characteristics can vary during the lifetime of an implant, mainly as a consequence of wear phenomena, with a reciprocal adaptation of mating surfaces.
Contact forces: Tribological investigations usually move from the analysis of the contact problem of mating surfaces that means the estimation of the contact pressure at the interface at a macro scale level. For this purpose, two approaches are usually adopted in the literature, based on analytical formulas or numerical methods. However, both approaches are founded on the fundamental concept that real bodies are not rigid but (under given conditions) behave elastically, meaning that they can deform when loaded and go back to the initial shape as soon as the load is removed. The elasticity of the bodies depends on the material elastic properties that, in simple cases, are characterized by two quantities: the elastic or Young’s modulus E and the Poisson’s ratio ν.
The most widely used analytical solution for the contact actions between non-conformal bodies is due to Heinrich Hertz[6] (1882) and quantifies the contact pressure and the contact area (Figure 4). Such a solution assumes that, when two spheres 1 and 2 are in contact, the interacting surface can be approximated by a plane circle of radius a, which depends on the load F (of magnitude |F| = F) on the sphere radii (r1 and r2) and the material properties (E1, ν1 and E2,ν2) according to the following equations:
Math 26
(2)
where
Math 27
(3)
Math 28
(4)
The sign in equation (3) should be plus for external spheres (as in Figure 4) and minus for a sphere in a cup. Accordingly, pressure distribution can be calculated as
Math 29
, with pm = 3F/2πa2 (5)
where pm is the maximum pressure, at the center of the contact area.
Although Hertz theory is based on the hypothesis of non-conformal surfaces (so that a<< r1,r2), it is also frequently applied to the hip joints, particularly for hard-on-hard couplings (defined in Figure 2).
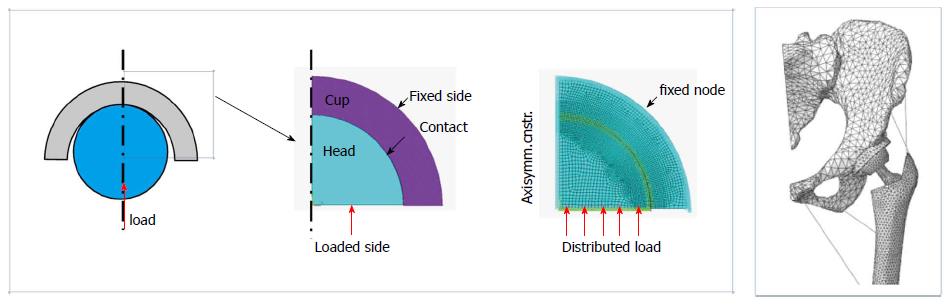
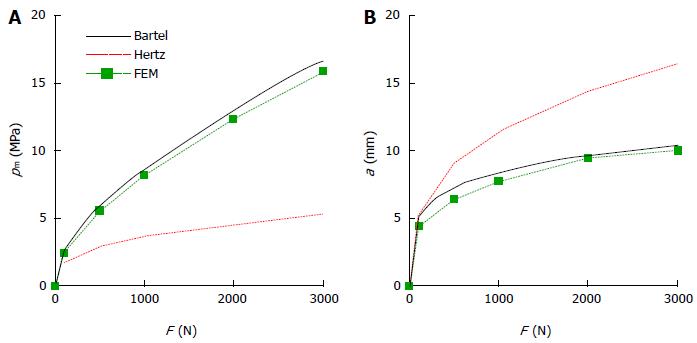
For soft-on-hard implants, several approximated analytical solutions were proposed, as in[7,8], usually assuming that the metal ball is much more rigid than the plastic cup, so that only the latter deforms. One of the most satisfactory solutions for a rigid sphere against a soft cup was proposed by Bartel et al[7] in 1985 based on geometrical considerations. However, the most widespread approach for solving contact problems is the finite element method (FEM)[9], actually implemented in a huge number of commercial codes. It can also deal with complex geometries and complex material behaviors (Figure 5).
In Figure 6, the contact radius and maximum pressure for a MoP implant, estimated according to different approaches, are compared. It can be observed that Hertz theory estimates a wider contact even larger than the cup radius and consequently a lower pressure peak. On the other side, an approximated solution by Bartel et al[7] appears to be in good agreement with FEM analyses obtained with the model shown in Figure 5[10].
It must be added that the above mentioned approaches hold at a macro scale level. In fact, at a microscopic scale, contact occurs among surface asperities (Figure 7), inducing higher stresses and strains, which can be the onset of microdamage as cracks, debris detachment and so on. Statistical theories of multiple asperities contact have been proposed in the literature, starting from the studies of Greenwood et al[11]. Their application to hip implants is still limited to a few studies[12].
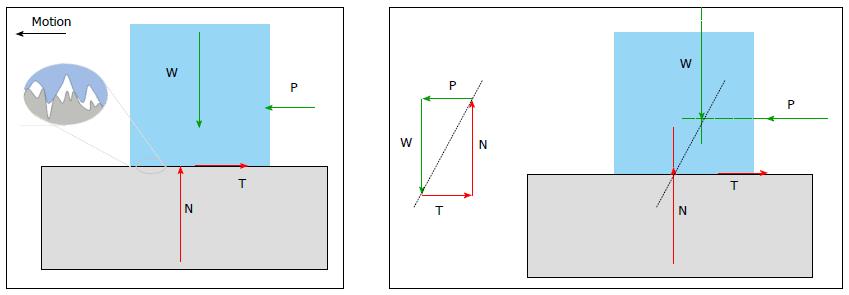
Friction is commonly defined as the resistance restraining the relative motion of two surfaces. It is usually classified as rolling or sliding friction, although they can be observed simultaneously. Sliding or kinetic friction is quantified through a coefficient, the coefficient of friction (COF) f, defined as the ratio between the magnitudes of the tangential/friction force T and the normal force N at the interface (Figure 8):
Math 30
(6)
Note that vector quantities are indicated with a normal font while their magnitude is in italics. The COF value, usually in the range 0.05-1, depends on the materials in contact, surface roughness, presence of a lubricant etc.
Equation (6) describes the first law of friction: friction force is proportional to the normal load. The second and third laws state that friction is independent of the apparent (nominal) contact area and of the sliding velocity, respectively. Such laws were derived from experimental observations but are not as general as usually expected; for example, polymers do not strictly obey them.
It is known that the major contribution to friction actions is due to the interaction between asperities, usually a combination of adhesion and deformation forces at the asperity junctions. The adhesion actions become detectable when the contact happens between clean surfaces, free from oxide or other surface films, which is not the case in implants, however. The deformation forces depend on the surface geometry and the material properties since asperities can deform elastically or plastically (permanently).
For metallic surfaces in air, contact is mainly through a thin film of oxide (apart from gold), whose thickness can be reduced by the normal load, and asperities tends to deform plastically. Also, temperature can play a role, both for oxide formation and phase transformation. Friction between ceramic materials is mainly affected by the elastic deformation of asperities. However, a wide variability of COF values can be found in the literature due to the role of environmental factors. Polymers have a peculiar viscoelastic behavior, thus deformation also induces dissipation (evident in rolling friction). Polymers usually obey the first law of friction, equation (6), only at low normal loads when the real contact area is proportional to N. At high loads or for very smooth surfaces, asperities are almost flattened due to the high compliance of the material and COF decreases while N increases.
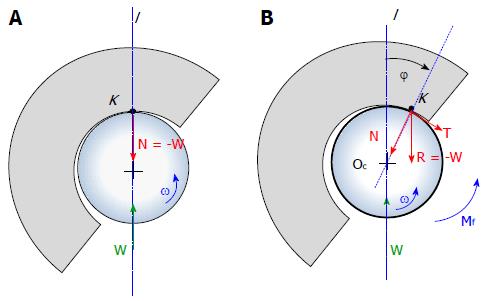
Finally, it is worth noting the peculiar behavior of a revolute/spherical joint with frictional contact, shown in Figure 9. Let us consider a pin rotating within a collar with constant angular velocity ω, under a load W through the center of the pin itself. In a smooth (frictionless) contact, the equilibrium of the pin is guaranteed by a normal (radial) force N = - W applied at the contact point K on the line of action of W. If friction cannot be neglected, the total contact force at the interface R, still with the same magnitude of W, is the sum of two components N and T, respectively normal and tangent to the surface at the contact point. Thus, in this case, K is shifted backwards in an angle ϕ = arctan(f), so that R restrains the motion and a torque Mf must be introduced to maintain the pin rotation.
As friction causes energy dissipation, resulting in heating or permanent surface deformation/damage, lubrication is usually introduced to assist motion. The same also happens in nature, for example in synovial joints or in the eyes.
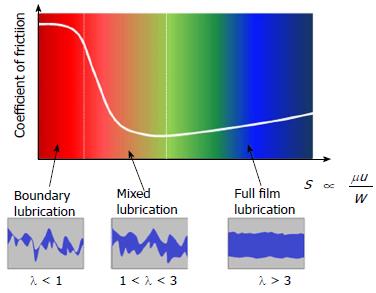
A lubricant, which can be a fluid or a solid, is interposed between the contact surfaces so that their asperities are completely separated or, at least, their interactions reduced, decreasing the frictional force. An estimate of the “distance” between the asperities of the mating surfaces is usually expressed by means of the parameter λ, which is the ratio between the minimum film thickness hmin and the composite roughness of the two surfaces:
Math 31
(7)
where Rq is the root mean squared roughness introduced in equation (1), subscripts 1 and 2 distinguish the two bodies in contact. It is worth noting that λ can also be estimated replacing Ra1,2 to Rq1,2 in equation (7), as they typically differ less than 10%.
The Stribeck curve, shown in Figure 10, describes the relationship between the COF and λ in three lubrication regimes: (1) Regime I (λ > 3): fluid film lubrication or hydrodynamic lubrication, where surfaces are completely separated; the pressure of the lubricant equilibrates the loading; (2) Regime II (1< λ <3): mixed-film lubrication, where only some asperities get in contact; the lubricant is pressurized and the loading is partly balanced by the direct contact between asperities and partly by the fluid hydrodynamic pressure; and (3) Regime III (1 > λ): boundary lubrication, where the lubricant thickness is of the order of the magnitude of molecules. The loading is carried by asperities which are protected by adsorbed molecules.
The abscissa in Figure 10 is denoted as a bearing characteristic number, or Sommerfeld number S, and for a given geometry is proportional to the dynamic viscosity of the lubricant μ, to the speed u and to the inverse of the load magnitude W, i.e.:
Math 32
(8)
Such factors determine the thickness of the lubricant meatus h, which can be estimated by means of analytical, numerical or empirical relationships.
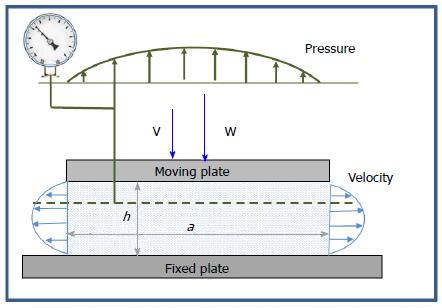
Hydrodynamic lubrication (HDL) is based on Reynolds equations, derived from the more general Navier-Stokes equations for fluid flow, whose solution usually implies simplifications and/or numerical methods. To understand what happens in HDL, let us consider a simple two-dimensional problem with two plates, separated by a fluid meatus, moving one over the other with a relative velocity u, as in Figure 11. It can be observed that the fluid particles adhering to the fixed plate have null velocity, while those adhering to the moving plate gain its velocity u. Thus, a gradient of velocity is achieved across each cross section of the meatus, approximately given by u/h. As arguably observed by Isaac Newton, such a gradient is related to the shear actions of the fluid (on other fluid particles as well as on the delimiting surfaces) through its viscosity:
Math 33
(9)
Thus, a resistance action T develops at the interface between the plates and the fluid (with an area A), having magnitude
T = Aτ (10)
and a force P is required to move the plate. However, until surfaces are parallel (Figure 11A), no hydrodynamic pressure generates within the interposed lubricant as it requires a variation of τ (or of the velocity gradient) along the interface. As suggested by experience, a lift or bearing action of the fluid develops when: (1) an angle of convergence of the surfaces is introduced; (2) the plate moves orthogonally to the surfaces (squeeze); or (3) there are different pressures at the endpoints.
For a fixed plane inclined bearing, as the meatus thickness h varies along the interface, velocity profiles in the cross sections change, as shown in Figure 11B, and according to Reynolds equation:
Math 34
, (11)
pressure develops within the fluid. By solving the above equation, the following relationships can be obtained:
Math 35
with
Math 36
and
Math 37
(12)
with the parameters a, h0 and h1 defined in Figure 11C and the pressure profiles in the meatus plotted in Figure 11D. Moreover, the normal load carrying capacity of the slider, balancing the total pressure on the moving plate, is:
Math 38
,
Math 39
(13)
that is maximum for m ≈ 1.2 and the frictional load:
Math 40
(14)
The COF is therefore given by the ratio f = T/W for this lubricated contact.
Squeeze lubrication (Figure 12) occurs when the two surfaces approach, pressurizing the lubricant, which balances the normal load:
Math 41
(15)
where v is the squeezing speed.
Things become much more complex for non-steady state or three-dimensional cases and numerical approaches are necessary to solve equations. The same happens when the description of the lubricant rheology needs to be improved, considering a non-Newtonian behavior (not obeying equation (9) even characterized by a temperature and pressure dependent viscosity (i.e., piezoviscosity), e.g.,
μ(p) =μ0 exp(αp) (16)
where μ0 and α are material constants.
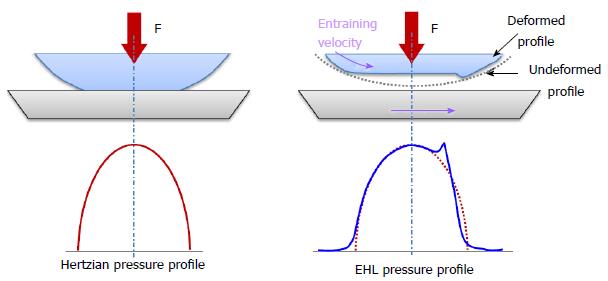
Moreover, when pressure increases, surface deformations cannot be neglected, thus contributing to what becomes elastohydrodynamic lubrication (EHL), which is typical of non-conformal contacts such as cams, gears, etc. In such cases, contact pressure resembles a Hertzian solution, as shown in Figure 13, differing in a tail at the inlet region and a peak at the outlet, where a reduction of the meatus thickness occurs.
The solution of EHL problems usually requires numerical methods. However, several empirical formulas were proposed in the literature for estimating the minimum film thickness. As an example, for a ball on plane case, the following relationships are usually applied[4]:
Math 42
(17)
Math 43
(18)
which hold for isoviscous and piezoviscous lubricants, respectively.
For spherical joints, such as the hip joint, two models are usually used for describing lubrication: a ball-in-socket and an equivalent ball-on-plane model[13,14]. The former employs Reynolds equations in spherical coordinates, where the elastic deformation can be estimated by means of the spherical fast Fourier transform or the multi-level multi-integration methods, both typically requiring a FE analysis for evaluating the deformation coefficients. On the other hand, ball-on-plane equivalent models, where the ball radius is req defined in equation (3), are much simpler but have been proved to provide satisfactory approximations, at least for hard-on-hard implants[13].
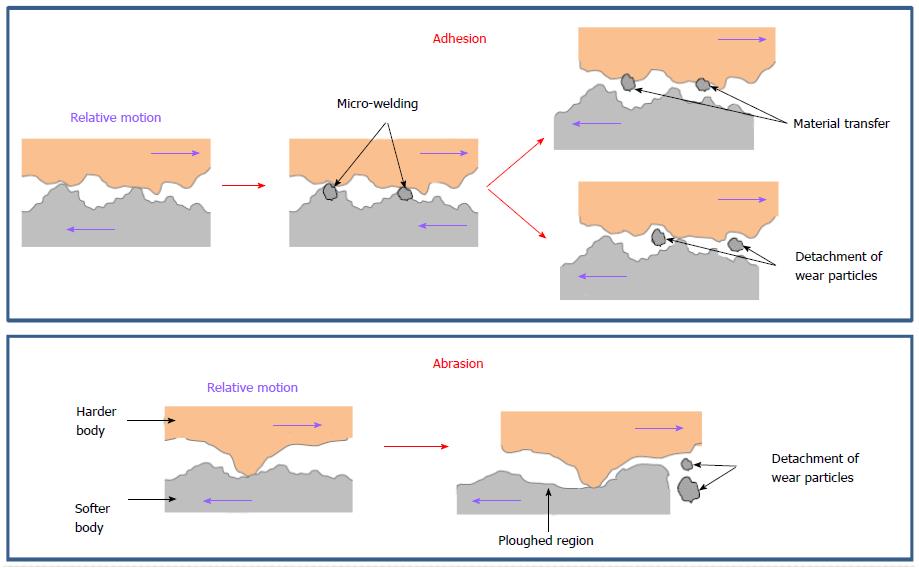
Wear is a surface damage combined with material loss or transfer between the articulating surfaces. Several wear mechanisms have been identified in the literature, here reduced to four types for simplicity: adhesion, abrasion, surface fatigue and tribochemical reactions (Figure 14).
Adhesive wear is used when local welding between asperities occurs, subsequently broken in the movement. Abrasion is due to the action of hard particles or asperities that plough the softer counterpart. Surface fatigue is due to repeated stress cycles in the subsurface material, which can be the onset of microcracks and debris detachment. Finally, tribochemical reactions, as corrosion, can be produced by a chemical reaction between surface materials and the interposed fluid.
Wear depends on many factors so it can be rather hard to predict which mechanism will affect the sliding bodies. This is done usually a posteriori and in many cases several types of wear are detected, as reported in[15] for knee replacements.
In this part, we will deal with sliding wear, meaning a combination of adhesive and abrasive wear, and in particular with the mathematical relationships that can be used to predict it, in terms of loss/worn volume V. Moving on experimental observations on metallic surfaces, in 1956 Archard proposed a rather simple wear law[16], known as Archard law, stating that:
V = K N s/H (19)
where N the normal load, H the material hardness, s the sliding distance and K the (adimensional) wear coefficient. Most frequently, a modified version with a dimensional wear coefficient k is employed
V = k N s (20)
also expressed as wear rate, by time-deriving and introducing the sliding speed v
dV/dt = kNv (21)
More detailed information is achieved by means of wear maps, describing the wear depth (linear wear h) at every single point of the surface.
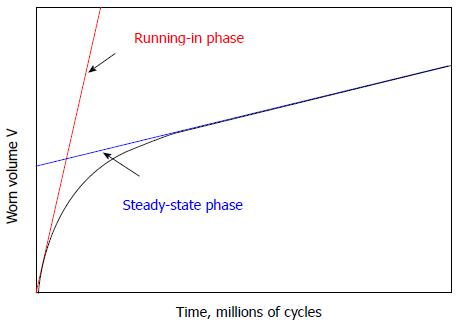
The wear coefficient is fundamental for estimating the wear strength of a coupling; for example, in dry contacts K can range from 1.3 10-7 to 7 10-3 for steel-mild steel and polyethylene-steel couples, respectively[16]. Such values refer to the steady state phase of the wear process, approximately above 1 million cycles. Higher wear coefficients are typically observed for the initial running-in phase, according to Figure 15.
Usually such coefficients are determined experimentally by means of pin-on-disc test rigs. However, as wear and both k-K are affected by many variables, from the lubrication regime, to temperature, to loading condition etc., it is important that wear tests reproduce the real operating conditions of the coupling. This is the reason why specific hip/knee simulators were developed, for replicating the loading and kinematic conditions of a gait cycle. However, it is still under discussion whether a simplified gait cycle, e.g., the one suggested by standard (ISO), is really representative of the joint operative conditions since remarkable differences are observed in worn volumes/surfaces of in vitro tested and retrieved implants.
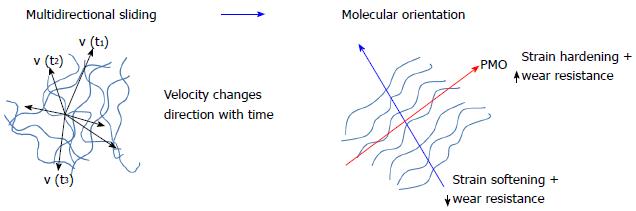
Despite being developed for metallic contacts, the Archard wear law is also widely applied to other materials. For ultra high molecular weight polyethylene (UHMWPE), a modified wear coefficient was proposed to take into account the peculiar anisotropic wear behavior of the polymer. In fact, it was observed that when UHMWPE is subjected to multidirectional sliding against a metallic counterface, the polymeric chains tend to align along a principal molecular orientation (PMO), thus increasing their wear strength in such a direction while reducing it in the orthogonal one (Figure 16)[17-20]. This phenomenon is usually denoted as “cross-shear” and has been extensively investigated in the last ten years as reviewed in[10]. Nevertheless, there is still a lack of understanding and many ongoing studies on the topic[10,21,22].
As wear tests are expensive and require long experimental procedures, predictive models are gaining interest, particularly for comparing different design solutions, geometrical characteristics and so on.
In this section, the general concepts described above are applied to hip implants in order to discuss their tribological behavior.
Firstly, some data on the most commonly used sizes of head diameter Dh and diametrical clearance Cl are summarized in Table 1. No distinction is made between normal and large head implants, the latter having Dh≥ 36 mm. In MoP and CoP implants, the cup thickness is also important and can vary in the range 5-18 mm.
| Head/cup | Dh (mm) | Cl (μm) |
| MoP | 22.2-44 | 160-400 |
| CoP | 22.2-36 | 160-400 |
| MoM | 22.2-54 | 50-150 |
| MoMRHR | 42-62 | 50-300 |
| CoC | 22.2-44 | 20-100 |
As already mentioned in Sec. 2, hip implants are made up of different types of materials, roughly distinguished between plastics, metals and ceramics, whose main mechanical properties are summarized in Table 2. The UHMWPE is the traditional plastic material for hip replacements, also adopted in the first THRs. In the last few decades, the mechanical properties of UHMWPE have been improved, leading to the highly cross-linked polyethylene (HXLPE)[23,24]. Indeed, the cross-linking of polymeric chains, accomplished by gamma or electron beam irradiation, significantly increases the wear resistance. However, an increase in the irradiation dose improves the wear resistance but only up to a threshold value. Moreover, the irradiation generates a certain amount of free radicals whose oxidation causes a degradation of the mechanical properties[24]. Consequently, the irradiation dose is typically kept low, below 10 MRad, and further treatments are used to control these drawbacks. In the first generation of HXLPE (1998), either melting or annealing was adopted[24]. The former allows elimination of free radicals, whilst the latter maintains mechanical properties. In order to achieve both results, a second generation of HXLPE has been recently introduced (2005)[23]. This material can be obtained by two different manufacturing processes: a sequential repetition of irradiation and annealing cycles; and the annealing of the material in presence of antioxidants such as vitamin E. The clinical follow up of both first and second generation of HXLPE cup has shown good outcomes with a reduction of wear rates up to 80% compared to the conventional UHMWPE[25,26].
| Material | E (GPa) | n | Ra (μm) | |
| P | UHMWPE | 0.5-1 | 0.4 | 0.1-2 |
| M | CoCrMo | 230 | 0.3 | 0.01-0.05 |
| C | Biolox delta | 350 | 0.26 | 0.001-0.005 |
The metal alloys used for hip implants encompass CoCrMo, CoCr and stainless steel. CoCrMo is the most widely used. This alloy can be obtained indifferently from wrought and cast materials, with or without heat treatment. Indeed, the manufacturing process has been revealed not to affect the mechanical properties of the alloy[27,28]. On the other hand, the carbon content covers a critical role in the wear resistance: high carbon content (> 0.15%) alloys actually in use exhibit a 64%-94% wear reduction compared to the low carbon content (< 0.08%) one[27-29].
Nowadays, the gold standard for ceramic materials is the Biolox delta, an alumina matrix composite recently introduced to the market (2007). The ceramic materials originally used for CoC implants, such as alumina (Al2O3) and zirconia (ZrO2), have been largely abandoned mainly because of their brittleness. Important advances in ceramic engineering technology have entailed the new material class of mixed oxide ceramics which combine the excellent tribological behavior of alumina with the good mechanical properties of yttrium-stabilized zirconia[30]. Biolox delta belongs to this class, made up of 82% alumina, 17% zirconia, 0.6% strontium oxide and 0.3% chromium oxide. Nanosized particles of yttrium-stabilized zirconia increase the strength and toughness of the alumina matrix by obstructing crack propagation. Also, strontium oxide contributes to improving the mechanical characteristics by generating platelet-like crystals able to deflect the cracks. On the other hand, chromium oxide improves the hardness and wear properties. The main limitations to a wide use of CoC implants are their high cost and the squeaking phenomenon.
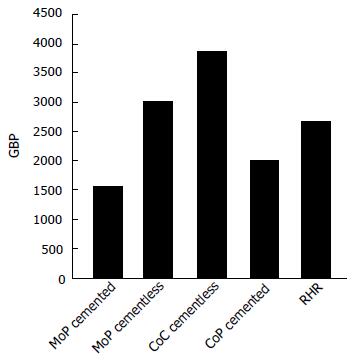
Indications of average list prices across manufacturers, taken from[31], are reported in Figure 17.
In order to provide some indications on the contact pressures and contact half-width in a hip implant, equations presented in Sec. 3.1.2 were applied to compare MoM and MoP couplings, assuming a normal load of 2500 N. Results are reported in Figure 18, as contour plots, for different values of the Dh and Cl. It can be observed that the pressure is a maximum for lower diameter and higher clearance, i.e., less conformal surfaces. Moreover, on equal implant size, the contact pressure is tenfold higher in MoM bearings compared to MoP, whilst the contact width is about four times lower. It is important to note that wear occurs only where contact pressure is not null, thus in MoP the worn areas are larger.
As already discussed in Sec. 3.2, for a hip implant the COF can vary largely with the system conditions, i.e., geometrical and material properties, lubricant type and kinematic/loading conditions. This has been demonstrated by several experimental studies on hip simulators devoted to friction measurements in simplified gait conditions (e.g., vertical load and flexion-extension motion)[32-36]. Table 3 provides typical values of COF for different bearing types, tested under the same conditions (flexion-extension of ± 25° at a frequency 1 Hz; sinusoidal load through 60% of the cycle, with a peak of 2 kN and a constant swing phase load of 100 N) and using two lubricant types (25% and 100% bovine serum)[32,33]. All the THRs were characterized by Dh = 28 mm and an averaged Cl = 126 μm, whilst MoMRHR implants had a Dh = 55 mm and a Cl = 92 μm. The highest COFs are observed for MoM implants with average values in the range 0.096-0.12. The MoM resurfacing implants are affected by lower friction compared to the MoM total ones, with average COFs approximately 0.079-0.098. On the other hand, similar COFs of about 0.04-0.064 are reported for MoP, CoP and CoC implants, with the lowest values observed in CoC.
| Head/cup | COF 25% Bovine serum | COF 100% Bovine serum |
| MoP | 0.062 (+ 0.008) | 0.064 (± 0.01) |
| CoP | 0.056 (+ 0.01) | 0.06 (± 0.012) |
| MoM | 0.12 (± 0.02) | 0.096 (± 0.012) |
| MoMRHR | 0.098 (± 0.02) | 0.079 (± 0.011) |
| CoC | 0.04 (+ 0.007) | 0.056 (± 0.01) |
The experimental studies reported in[32-35] describe how the COF is affected by the system conditions: the higher the head and clearance, the lower the COF, since more conformal bearings promote lubrication. Moreover, the higher the load (i.e., swing phase load), the higher the COF[32,33]. Also, the lubricant type strongly affects the COF, as highlighted in Table 3. In particular, a higher concentration of proteins in the lubricant (i.e., in 100% bovine serum) increases the COF for all implant types, with the exception of MoM ones which probably take advantage of a protein protective layer deposited over the bearing surfaces. Consequently, reliable friction measurements require the use of lubricants with a rheological behavior as much as possible similar to the synovial fluid. It is worth noting that 25% bovine serum is more widely used than 100% in simulator studies.
As previously discussed, lubrication, like friction, is a complex phenomenon which depends on the tribological, chemical and mechanical conditions of the system. Thus, the lubrication performance of a hip replacement assessed from a specific test condition cannot be generalized. Usually, the reference task for hip and knee implants is a gait cycle, sometimes with simplified loading/kinematic condition.
While friction and wear phenomena are mainly investigated by means of an experimental approach, the literature has a large number of theoretical studies focused on the lubrication of hip replacements, as reviewed in[37], and only a few experimental investigations (e.g.,[38-40]). Lubrication studies, both theoretical and experimental, aim to estimate the minimum film thickness, comparing it to the composite roughness of the bearing surfaces and assessing the lubrication regime. It is worth mentioning that the experimental approach exploits a resistivity technique to measure the thickness of the meatus, usually performing in in vitro measurements on hip simulators.
Typical values of minimum film thickness (equation (17)), λ ratio and indications of the lubrication regime are summarized in Table 4 for the hip implants described in Table 1, adopting the material/surface properties of Table 2 (for plastic E = 1GPa).It can be observed that implants with the plastic cup (MoP and CoP) are subjected to a boundary/mixed lubrication regime, almost independently from the size: hmin results comparable to Ra and hence λ values remain low, inferior to 1. MoM hip implants exhibit only a slightly improved lubrication, with λ values in the range 0.6-2.9. Indeed, although metallic surfaces have a Ra lower than the plastic ones, they have a thinner lubricant film because of their lower elasticity. As confirmed by experimental evidence[39], even although the prevailing lubrication mode of MoM implants is mixed, they can span all lubrication regimes, from the boundary to fluid film. Both theoretical and experimental studies demonstrate the high sensitivity of the MoM lubrication regime to implant geometry[38,40-42], bearing design/manufacturing[42] and loading/kinematic conditions[43,44]. In particular, increased head size coupled with decreased clearance has been proved to improve lubrication, as happens both for MoM large head and RHR, which can operate under a fluid-film regime (Table 4)[38,40-42]. The best lubrication behavior is estimated for CoC implants[38]; their high surface finishing (i.e., very low roughness) balances the low film thickness, guaranteeing a fluid-film regime (λ in the range 5.3-28.3). It is worth noting that the clearance must be dimensioned properly, avoiding both large values which would lead to the boundary regime and low values, which might cause edge contact and thus lubricant starvation.
| Head/cup | hmin (μm) | Ra (μm) | λ | Lubricationregime |
| MoP | 0.065-0.144 (0.105) | 0.1-2 | 0.1-1 | Boundary to Mixed |
| CoP | 0.076-0.107 (0.092) | 0.1-2 | 0.05-0.9 | Boundary to Mixed |
| MoM | 0.020-0.061 (0.041) | 0.014-0.071 | 0.6-2.9 | Boundary to Mixed |
| MoMRHR | 0.082-0.049 (0.066) | 0.014-0.071 | 0.9-4.6 | Boundary to Fluid-film |
| CoC | 0.035-0.045 (0.04) | 0.0014-0.0071 | 5.7-28.3 | Fluid-film |
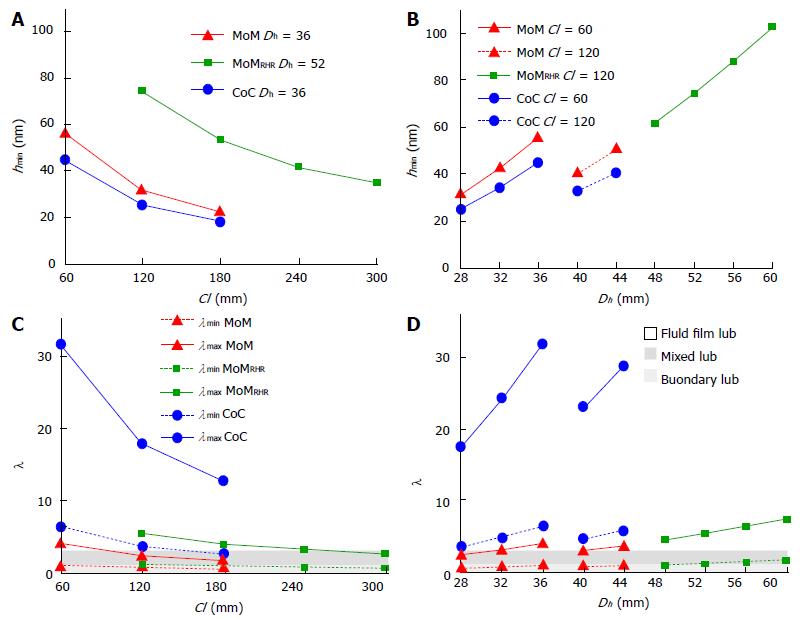
In order to clarify the key role of geometry and materials on the lubrication regime of hard-on-hard implants, some meaningful results from numerical simulations are portrayed in Figure 19[45]. The minimum film thickness and the lubrication regime of three bearing types (MoM, MoMRHR and CoC) are estimated by means of a simplified 3D ball-on-plane EHL model, assuming the synovial fluid as lubricant (μ = 2.5 mPa s) and typical gait conditions (vertical load W = 2 kN, angular velocity in flexion-extension ω = 2 rad/s). The effect of diametrical clearance Cl (Figure 19A, C) and head diameter Dh (Figure 19) was investigated, confirming that lower Cl and higher Dh, which means more conformal bearings, promote the lubrication regime causing thicker film thickness (Figure 19A, B) and higher λ values (Figure 19C, D). On equal Cl or Dh, the minimum film thickness is highest in MoMRHR implants and lowest in CoC ones, the ceramic being harder than the metals. On the other hand, for their very smooth surfaces, CoC implants turn out to be the only ones that undergo fluid film lubrication in the simulated gait conditions, almost independently from their dimensions. It is worth noting that these results are in good agreement with those obtained from empirical formula (Table 4).
As far as the relevant effect of the geometry on the lubrication is concerned, recently a novel MoM implant design characterized by a non-spherical bearing surface was proposed in[46,47]. Numerical EHL simulations demonstrate the superiority of the non-spherical couple which significantly improves the lubrication by increasing the couple conformity in the loaded area.
It is worth mentioning that, although EHL predictions are very useful for carrying out comparative analysis on implant performances and hence for implant design optimization, some of the recent literature studies suggest that protein-containing fluids, such as synovial fluid, do not obey classical Newtonian EHL models[48,49]. This aspect is particularly relevant for MoM implants, as mentioned in Sec. 4.4. According to experimental observations[48,49], two main effects should be considered when a metallic surface is lubricated by a protein-containing solution: the adsorption of a protective protein layer on the surface; and the formation of a high-viscosity film in the inlet region due to protein molecule aggregation, which allows a thick film particularly at low speed. As this complex phenomenon is highly dependent both on time and shear rate, the classical Newtonian model [equation (9)] is no longer valid.
Wear can be considered the most relevant tribological phenomenon from a clinical point of view. Indeed, wear is recognized as the main reason of hip implant failure, causing inflammatory reactions and osteolysis, which can lead to implant loosening. Compared to friction and lubrication, experimentally investigated mainly in vitro, wear can also be studied in vivo (e.g., radiographically) and ex vivo (from retrieved implants), providing a clinical insight of the tribological life of the implant. Typical values of the linear (hclin) and volumetric (Vclin) wear rates observed clinically are summarized in Table 5. It soon becomes apparent that the wear rates are very scattered, probably because of the variability of the clinical scenarios involving both patient characteristics (age, gender, body weight index, daily activities) and their physiological/pathological conditions.
| Head/cup | hclin (μm/Mc) | Vclin (mm3/Mc) |
| MoP | 50-500 (50) | 10-500 (80) |
| CoP | 30-150 | 15-50 |
| MoM (RI) | 1-50 | 0.1-25 |
| MoM (SS) | 0.1-1 | 0.05-4 |
| MoMRHR (RI + SS) | 0.2-10 | 0.2-2.9 |
| MoMRHR (ADT) | 1.5-46 | 0.2-95 |
| CoC | 0.01-1 | 0.005-2 |
Soft-on-hard couples are affected by the highest wear rates, in agreement with the estimated boundary/mixed lubrication regime (see Sec. 4.4-5). In particular, MoP implants are characterized by average hclin and Vclin of about 50 μm/y and 80 mm3/y, respectively. Wear rates of MoM implants are definitely lower, even up to 2 orders of magnitude. Indeed, although a prevalent mixed/boundary lubrication regime is predicted for MoM and MoP implants, the former exhibit a higher wear resistance due to hard surfaces and protein boundary layers which protect the bearing surfaces. The biphasic wear behavior of MoM is highlighted: passing from the running-in to the steady-state phase, hclin decreases from 1-50 to 0.1-1 μm/y, while Vclin decreases from 0.1-25 to 0.05-4 mm3/y. The wear rate of resurfacing implants is a debated issue. Some successful MoMRHR devices have showed lower wear rates in agreement with the fluid-film lubrication, predicted under favorable conditions, with hclin and Vclin in the ranges 0.2-10 μm/y and 0.2-2.9 mm3/y, respectively[50]. On the other hand, an important percentage of these implants, showing adverse tissue reaction (ADT) at the moment of the explantation, were subjected to high wear rates, in the ranges of 1.5-46 μm/y and 0.2-95 mm3/y[51]. Such values are very concerning as the wear of metallic surfaces causes the release of dangerous toxic metallic ions[51,52]. One of the main causes of MoMRHR excessive wear rates is a too steep cup inclination which leads to the edge loading, i.e., the collision between the femoral head and the rim of the acetabular cup (Figure 20). Indeed, the edge loading causes concentrated high contact pressures and, furthermore, can cause the disruption of the lubricant.
CoC implants are recognized as the most wear resistant thanks to their very hard surfaces and effective lubrication. Under normal conditions, extremely low wear rates have been found for the ceramic bearings of about 0.01-1 μm/y and 0.005-2 mm3/y. Furthermore, ceramic debris are bioinert and not clinically relevant. On the other side, one of the current main drawbacks of CoC is not the wear but the squeaking, i.e., the audible sound generated by these implants during the motion. The lubricant starvation, caused by edge loading, seems to be one of the main cause of this phenomenon[30].
Beyond clinical studies, experimental in vitro wear analyses remain fundamental for characterizing the wear of an implant, comparing different bearing types, as well as for the screening of innovative materials and implant design optimization. Such studies are carried out both in traditional pin-on-plate/pin-on-disk test machines and in hip joint simulators, generally simulating physiological simplified gait conditions. Recently, multidirectional pin-on-plate devices have also been developed for investigating the cross-shear of UHMWPE. In the attempt to quantify the cross-shear, many wear tests have been carried out, leading to new expressions of the wear coefficient as a function of the multidirectional sliding and to new wear laws[10]. A few studies have been recently carried out on MoMRHR implants, confirming the influence of the cup orientation on wear as it can cause edge loading[53].
Analytical and numerical studies support experimental analyses, allowing long term wear predictions at low cost[37]. Most of them have been applied to MoP implants and only few to MoM and MoMRHR implants. However, one critical aspect of such wear models is the selection of suitable values of the wear coefficient since, as mentioned in Sec. 3.4, it depends on many factors and can vary both spatially and in time. As a confirmation, the wear coefficient values are very scattered in the literature. Typical k ranges are the following: 10-7-10-6 mm3/(N m) for MoP; 10-9-10-7 mm3/(N m) for MoM; and 10-10-10-8 mm3/(N m) for CoC implants. However, numerical predictions are in good agreement with the experimental ones obtained from a hip simulator, whilst underestimating the clinical ones, probably because they do not simulate all the in vivo implant conditions, i.e., different daily activities in addition to walking.
The effect of the geometry and the loading/kinematic conditions on wear has been widely investigated, providing findings in agreement with the friction and lubrication studies.
Some major trends are recognized in the implant of a hip prosthesis which reflects the clinical outcomes of hip arthroplasty and thus the revision risk associated with each implant type. A meaningful statistical analysis on this topic is provided by the National Joint Registry of England, Wales and Northern Ireland[3] which has collected data on clinical procedures and outcomes since 2003. This source has been adopted as the main reference of this section as it is one of the more extended and complete registries to the best of our knowledge.
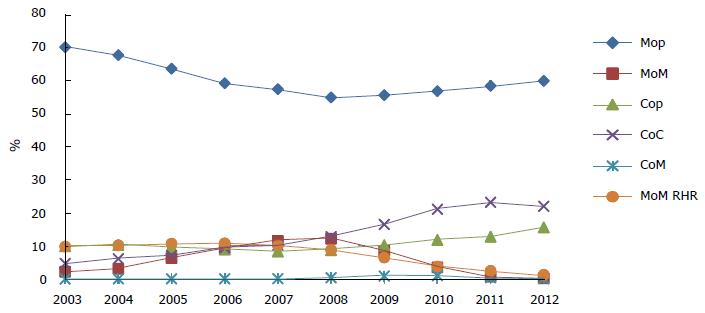
The trends of bearing couplings from 2003 to 2012, expressed as percentages of implant type per year, are depicted in Figure 21. MoP implants, the traditional ones, are still the most widely used, covering about the 60% of all procedures in 2012. This is partly due to the introduction of the high wear resistant HXLPE (see Sec. 4.2). The use of the ceramic components is increasing, with an increase of 22% of CoC and 16% of CoP implants in 2012. Also in this case, the improvements in material properties leading to Biolox delta characterized by a high mechanical strength and high wear resistance have been a determinant. As mentioned above, the wear of ceramic implants is irrelevant and one of the main concerns in their employment is still the squeaking. It is worth noting that the incidence of squeaking reported in the literature varies in the range < 1%-21%, depending on how the sound is defined[30,54]. On the contrary, the use of metal bearings, both total and resurfacing, has decreased in the last few years. After reaching a peak between 2006 and 2008, these implants have been largely abandoned, their use now reduced to 1.5%. This trend is due to the ongoing concerns on pseudotumors caused by toxic metallic ions and the high failure rates of large head and RHRs related to the edge loading, as discussed in Sec. 4.6. Certainly, the decreased implantation of these implants has been further enhanced by the voluntary recall of the RHR system ASR by DePuy (2010). An additional reason behind such percentages can be found in implant costs (Figure 17).
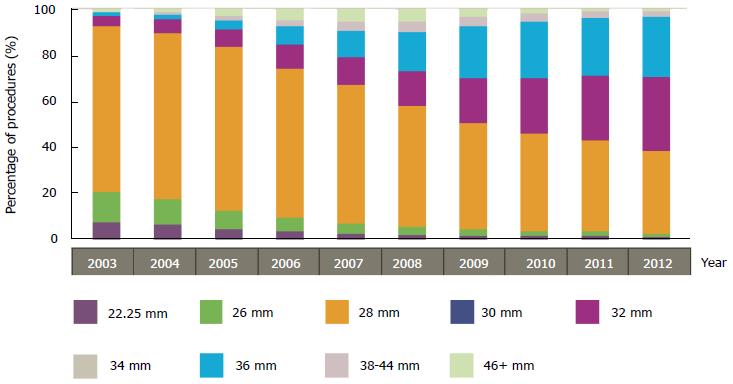
In terms of femoral head size, the trend is characterized by a gradual increase in the use of larger heads, which is in agreement with both theoretical and experimental findings, as bigger implants, i.e., more conformal couples, promote the lubrication and prevent dislocation (Figure 22). The 28 mm heads, mostly used in 2003, have been declining in favor of 32 and 36 mm heads. Whilst the increase of 32 mm heads is continuing, the 36 mm heads trend has been slightly reversing since 2010, which reflects the actual concerns on large head MoM THRs and MoMRHR.
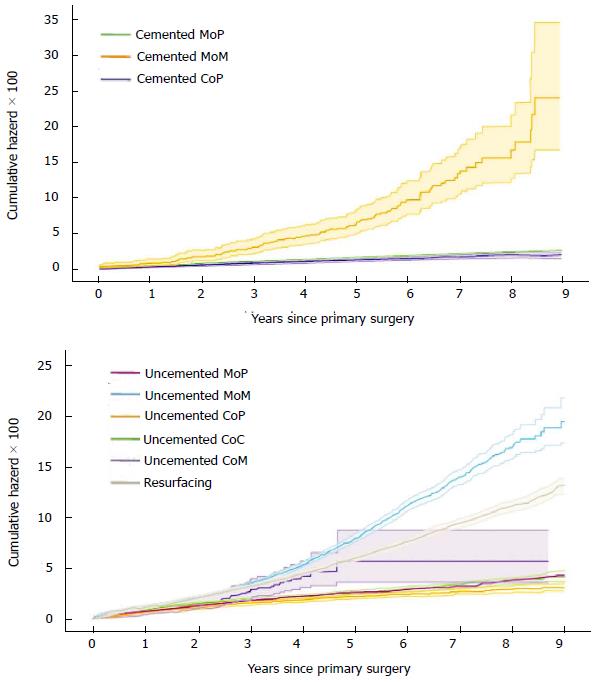
In order to complete this overview on hip implant procedures, the revision risk for hip articulation type is provided in Figure 23. The trends are in full agreement with the above discussion. The highest revision risk (up to 15%) is reported for MoM bearings, with revision rates of 17.7% and 12.3% for cementless total and resurfacing implants, respectively, and up to 33% for the cemented ASR RHRs. The lowest revision rates, less than 2%, were observed for MoP and CoP implants and similar performances were also reported for CoC.
The present review aims to describe the biotribology of hip replacements both qualitatively and quantitatively. The fundamental concepts of tribology, provided in the first part particularly for non-specialists, are applied to artificial hip joints, thus allowing interpretation of the actual trends in hip arthroplasty. The interest in larger head sizes, the increasing use of CoC implants, the squeaking of hard-on-hard couples and even the high failure rates of RHR implants are considered and explained from a tribological point of view.
The wide discussion on the tribological features of each implant type highlights how friction, lubrication and wear are strongly interconnected and cannot be discerned one from the other: the study of biotribology of hip implants should thus be treated as a whole, where each aspect helps, completes and confirms the understanding of the others. Moreover, such tribological features depend on the characteristics of the system taken into consideration, the materials (e.g., Young’s modulus, hardness), geometry (e.g., head diameter, clearance, surface finishing), kinematic and loading conditions and lubricant type. Consequently, for each bearing type, friction, lubrication and wear vary during a single activity as well as in the implant lifetime as the patient characteristics, lifestyle and wear itself modify the tribological scenario continuously. These considerations raise some concerns of the suitability of in vitro tests for hip implants since simplified gait cycles can be too far from the effective implant working conditions.
This paper points out the complexity of biotribology science and its fundamental role in analyzing and improving hip implant design, as well as the need for further investigations in order to improve hip arthroplasty outcomes.
P- Reviewer: Azzoni R, Meng QE S- Editor: Song XX L- Editor: Roemmele A E- Editor: Lu YJ
| 1. | Dowson D. History of tribology. 2nd ed. London: John Wiley & Sons 1998; . |
| 3. | Available from: http: //www.njrcentre.org.uk. |
| 4. | Hutchings I, Shipwa P, Tribology . 2nd ed. Butterworth-Heinemann Ltd. London: John Wiley & Sons 2007; . |
| 5. | Sudeep I, Nosonovsky M, Satish Vasu K, Michael RL, Pradeep LM. Tribology for Scientists and Engineers. Springer-Verlag. London: John Wiley & Sons 2013; . |
| 6. | Hertz HR. On Contact Between Elastic Bodies. Germany, Leipzig: Gesammelte Werke (Collected works) 1882; . |
| 7. | Bartel DL, Burstein AH, Toda MD, Edwards DL. The effect of conformity and plastic thickness on contact stresses in metal-backed plastic implants. J Biomech Eng. 1985;107:193-199. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 216] [Cited by in RCA: 150] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 8. | Li G, Sakamoto M, Chao EY. A comparison of different methods in predicting static pressure distribution in articulating joints. J Biomech. 1997;30:635-638. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 62] [Cited by in RCA: 46] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 9. | Zienkiewicz OC, Taylor RL, Zhu JZ. The Finite Element Method: Its Basis and Fundamentals. 7th ed. United Kingdom: Butterworth-Heinemann 2013; . |
| 10. | Mattei L, Di Puccio F, Ciulli E. A comparative study on wear laws for soft-on-hard hip implants using a mathematical wear model. Tribol Int. 2013;63:66-77. [DOI] [Full Text] |
| 11. | Greenwood JA, Williamson JBP. Contact of nominally flat surfaces. Proc R Soc Lond A Math Phys Sci. 1966;295:300-319. [RCA] [DOI] [Full Text] [Cited by in Crossref: 3502] [Cited by in RCA: 3499] [Article Influence: 59.3] [Reference Citation Analysis (0)] |
| 12. | Suhendra N, Stachowiak GW. Computational model of asperity contact for the prediction of UHMWPE mechanical and wear behaviour in total hip joint replacements. Tribol Lett. 2007;25:9-22. [DOI] [Full Text] |
| 13. | Mattei L, Ciulli E, Di Puccio F, Piccigallo B. EHL modelling of hard-on-hard hip implants: comparison of total and resurfacing hip implants (Proceedings of the 17th Congress of the European Society of the Biomechanics; 2010 Jul 5-8). United Kingdom: Edinburgh 2010; . |
| 14. | Wang WZ, Wang FC, Jin ZM, Dowson D, Hu YZ. Numerical lubrication simulation of metal-on-metal artificial hip joint replacements: Ball-in-socket model and ball-on-plane model. P I Mech Eng J-J Eng. 2009;223:1073-1082. [DOI] [Full Text] |
| 15. | Hood RW, Wright TM, Burstein AH. Retrieval analysis of total knee prostheses: a method and its application to 48 total condylar prostheses. J Biomed Mater Res. 1983;17:829-842. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 360] [Cited by in RCA: 307] [Article Influence: 7.3] [Reference Citation Analysis (0)] |
| 16. | Archard JF, Hirst W. The wear of metals under unlubricated conditions. Proc R Soc Lond A Math Phys Sci. 1956;236:397-410. [RCA] [DOI] [Full Text] [Cited by in Crossref: 554] [Cited by in RCA: 570] [Article Influence: 20.4] [Reference Citation Analysis (0)] |
| 17. | Wang A, Sun DC, Yau SS, Edwards B, Sokol M, Essner A, Polineni VK, Stark C, Dumbleton JH. Orientation softening in the deformation and wear of ultra-high molecular weight polyethylene. Wear. 1997;203-204:230-241. [DOI] [Full Text] |
| 18. | Wang A, Essner A, Klein R. Effect of contact stress on friction and wear of ultra-high molecular weight polyethylene in total hip replacement. Proc Inst Mech Eng H. 2001;215:133-139. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 87] [Cited by in RCA: 45] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 19. | Barbour PSM, Barton RC, Fisher N. The influence of contact stress on the wear of UHMWPE for total replacement hip prostheses. Proceedings of the 10th International Conference on Wear of Materials. Wear. 1995;181-183:250-257. [DOI] [Full Text] |
| 20. | Turell M, Wang A, Bellare A. Quantification of the effect of cross-path motion on the wear rate of ultra-high molecular weight polyethylene. Wear. 2003;255:1034-1039. [DOI] [Full Text] |
| 21. | Schwenke T, Wimmer MA. Cross-Shear in Metal-on-Polyethylene Articulation of Orthopaedic Implants and its Relationship to Wear. Wear. 2013;301:168-174. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 20] [Cited by in RCA: 17] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 22. | Korduba LA, Wang A. The effect of cross-shear on the wear of virgin and highly-crosslinked polyethylene. Wear. 2011;271:1220-1223. [DOI] [Full Text] |
| 23. | Dumbleton JH, D’Antonio JA, Manley MT, Capello WN, Wang A. The basis for a second-generation highly cross-linked UHMWPE. Clin Orthop Relat Res. 2006;453:265-271. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 186] [Cited by in RCA: 169] [Article Influence: 8.9] [Reference Citation Analysis (0)] |
| 24. | McKellop H, Shen FW, Lu B, Campbell P, Salovey R. Development of an extremely wear-resistant ultra high molecular weight polyethylene for total hip replacements. J Orthop Res. 1999;17:157-167. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 573] [Cited by in RCA: 453] [Article Influence: 17.4] [Reference Citation Analysis (0)] |
| 25. | D’Antonio JA, Capello WN, Ramakrishnan R. Second-generation annealed highly cross-linked polyethylene exhibits low wear. Clin Orthop Relat Res. 2012;470:1696-1704. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 57] [Cited by in RCA: 52] [Article Influence: 4.0] [Reference Citation Analysis (0)] |
| 26. | Reynolds SE, Malkani AL, Ramakrishnan R, Yakkanti MR. Wear analysis of first-generation highly cross-linked polyethylene in primary total hip arthroplasty: an average 9-year follow-up. J Arthroplasty. 2012;27:1064-1068. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 50] [Cited by in RCA: 47] [Article Influence: 3.6] [Reference Citation Analysis (0)] |
| 27. | Chan FW, Bobyn JD, Medley JB, Krygier JJ, Tanzer M. The Otto Aufranc Award. Wear and lubrication of metal-on-metal hip implants. Clin Orthop Relat Res. 1999;369:10-24. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 262] [Cited by in RCA: 177] [Article Influence: 6.8] [Reference Citation Analysis (0)] |
| 28. | Dowson D, Hardaker C, Flett M, Isaac GH. A hip joint simulator study of the performance of metal-on-metal joints: Part I: The role of materials. J Arthroplasty. 2004;19:118-123. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 15] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 29. | Firkins PJ, Tipper JL, Saadatzadeh MR, Ingham E, Stone MH, Farrar R, Fisher J. Quantitative analysis of wear and wear debris from metal-on-metal hip prostheses tested in a physiological hip joint simulator. Biomed Mater Eng. 2001;11:143-157. [PubMed] |
| 30. | Jenabzadeh A-R, Pearce SJ, Walter WL. Total hip replacement: ceramic-on-ceramic. Semin Arthroplasty. 2012;23:232-240. [RCA] [DOI] [Full Text] [Cited by in Crossref: 15] [Cited by in RCA: 9] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 31. | NICE draft guidance update on hip replacement and resurfacing recommends more reliable artificial joints. 2013;. Available from: http: //www.nice.org.uk/newsroom/pressreleases/NICEDraftGuidanceRecommendsMoreReliableArtificialJoints.jsp. |
| 32. | Brockett C, Williams S, Jin Z, Isaac G, Fisher J. Friction of total hip replacements with different bearings and loading conditions. J Biomed Mater Res B Appl Biomater. 2007;81:508-515. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 117] [Cited by in RCA: 84] [Article Influence: 4.7] [Reference Citation Analysis (0)] |
| 33. | Brockett CL. A comparison of friction in 28 mm conventional and 55 mm resurfacing metal-on-metal hip replacements. P I Mech Eng C-J Mec. 2007;221:391-398. [DOI] [Full Text] |
| 34. | Flanagan S, Jones E, Birkinshaw C. In vitro friction and lubrication of large bearing hip prostheses. Proc Inst Mech Eng H. 2010;224:853-864. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 13] [Cited by in RCA: 14] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 35. | Scholes SC, Unsworth A. Comparison of friction and lubrication of different hip prostheses. Proc Inst Mech Eng H. 2000;214:49-57. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 132] [Cited by in RCA: 84] [Article Influence: 3.4] [Reference Citation Analysis (0)] |
| 36. | Mattei L, Di Puccio F. Wear simulation of metal-on-metal hip replacements with frictional contact. J Tribol. 2013;135:1-11. [DOI] [Full Text] |
| 37. | Mattei L, Di Puccio F, Piccigallo B, Ciulli E. Lubrication and wear modelling of artificial hip joints: a review. Tribol Int. 2011;44:532–549. [DOI] [Full Text] |
| 38. | Smith SL, Dowson D, Goldsmith AAJ, Valizadeh R, Colligon JS. Direct evidence of lubrication in ceramic-on-ceramic total hip replacements. P I Mech Eng C-J Mec. 2001;215:265-268. [DOI] [Full Text] |
| 39. | Dowson D, Mc Nie CM, Goldsmith AAJ. Direct experimental evidence of lubrication in metal-on-metal total hip replacement. P I Mech Eng J-J Eng. 2000;214:75-86. [DOI] [Full Text] |
| 40. | Smith SL, Dowson D, Goldsmith AAJ. The lubrication of metal-on-metal total hip joints: A slide down the Stribeck curve. P I Mech Eng J-J Eng. 2001;215:483-493. [DOI] [Full Text] |
| 41. | Liu F, Jin Z, Roberts P, Grigoris P. Importance of head diameter, clearance, and cup wall thickness in elastohydrodynamic lubrication analysis of metal-on-metal hip resurfacing prostheses. Proc Inst Mech Eng H. 2006;220:695-704. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 66] [Cited by in RCA: 67] [Article Influence: 3.5] [Reference Citation Analysis (0)] |
| 42. | Liu F, Jin Z, Roberts P, Grigoris P. Effect of bearing geometry and structure support on transient elastohydrodynamic lubrication of metal-on-metal hip implants. J Biomech. 2007;40:1340-1349. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 17] [Cited by in RCA: 18] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 43. | Gao L, Wang F, Yang P, Jin Z. Effect of 3D physiological loading and motion on elastohydrodynamic lubrication of metal-on-metal total hip replacements. Med Eng Phys. 2009;31:720-729. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 28] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 44. | Smith SL, Unsworth A. Simplified motion and loading compared to physiological motion and loading in a hip joint simulator. Proc Inst Mech Eng H. 2000;214:233-238. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 26] [Cited by in RCA: 27] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 45. | Mattei L, Di Puccio F, Piccigallo B, Ciulli E. Elastohydrodynamic lubrication in total and resurfacing hip implants: effect of materials and geometries (Proceedings of the 6th World Congress on Biomechanics; 2010 Aug 1-6). Singapore: Springer 2010; . |
| 46. | Meng Q, Gao L, Liu F, Yang P, Fisher J, Jin Z. Contact mechanics and elastohydrodynamic lubrication in a novel metal-on-metal hip implant with an aspherical bearing surface. J Biomech. 2010;43:849-857. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 21] [Cited by in RCA: 23] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 47. | Meng QE, Liu F, Fisher J, Jin ZM. Transient elastohydrodynamic lubrication analysis of a novel metal-on-metal hip prosthesis with a non-spherical femoral bearing surface. Proc Inst Mech Eng H. 2011;225:25-37. [PubMed] |
| 48. | Fan J, Myant CW, Underwood R, Cann PM, Hart A. Inlet protein aggregation: a new mechanism for lubricating film formation with model synovial fluids. Proc Inst Mech Eng H. 2011;225:696-709. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 50] [Cited by in RCA: 30] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 49. | Myant C, Cann P. In contact observation of model synovial fluid lubricating mechanisms. Tribol Int. 2013;63:97-104. [DOI] [Full Text] |
| 50. | Takamura KM, Amstutz HC, Lu Z, Campbell PA, Ebramzadeh E. Wear analysis of 39 conserve plus metal-on-metal hip resurfacing retrievals. J Arthroplasty. 2014;29:410-415. [RCA] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 18] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 51. | Gill HS, Grammatopoulos G, Adshead S, Tsialogiannis E, Tsiridis E. Molecular and immune toxicity of CoCr nanoparticles in MoM hip arthroplasty. Trends Mol Med. 2012;18:145-155. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 116] [Cited by in RCA: 115] [Article Influence: 8.8] [Reference Citation Analysis (0)] |
| 52. | Xia Z, Kwon YM, Mehmood S, Downing C, Jurkschat K, Murray DW. Characterization of metal-wear nanoparticles in pseudotumor following metal-on-metal hip resurfacing. Nanomedicine. 2011;7:674-681. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 55] [Cited by in RCA: 45] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 53. | Saikko V, Ahlroos T, Revitzer H, Ryti O, Kuosmanen P. The effect of acetabular cup position on wear of a large-diameter metal-on-metal prosthesis studied with a hip joint simulator. Tribol Int. 2013;60:70-76. [DOI] [Full Text] |
| 54. | Jarrett CA, Ranawat AS, Bruzzone M, Blum YC, Rodriguez JA, Ranawat CS. The squeaking hip: a phenomenon of ceramic-on-ceramic total hip arthroplasty. J Bone Joint Surg Am. 2009;91:1344-1349. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 192] [Cited by in RCA: 172] [Article Influence: 10.8] [Reference Citation Analysis (0)] |