Published online Feb 7, 2009. doi: 10.3748/wjg.15.531
Revised: August 3, 2008
Accepted: August 10, 2008
Published online: February 7, 2009
The simulation of the dynamics of viral infections by mathematical equations has been applied successfully to the study of viral infections during antiviral therapy. Standard models applied to viral hepatitis describe the viral load decline in the first 2-4 wk of antiviral therapy, but do not adequately simulate the dynamics of viral infection for the following period. The hypothesis of a constant clearance rate of the infected cells provides an unrealistic estimation of the time necessary to reach the control or the clearance of hepatitis B virus (HBV)/hepatitis C virus (HCV) infection. To overcome the problem, we have developed a new multiphasic model in which the immune system activity is modulated by a negative feedback caused by the infected cells reduction, and alanine aminotransferase kinetics serve as a surrogate marker of infected-cell clearance. By this approach, we can compute the dynamics of infected cells during the whole treatment course, and find a good correlation between the number of infected cells at the end of therapy and the long-term virological response in patients with chronic hepatitis C. The new model successfully describes the HBV infection dynamics far beyond the third month of antiviral therapy under the assumption that the sum of infected and non-infected cells remains roughly constant during therapy, and both target and infected cells concur in the hepatocyte turnover. In clinical practice, these new models will allow the development of simulators of treatment response that will be used as an “automatic pilot” for tailoring antiviral therapy in chronic hepatitis B as well as chronic hepatitis C patients.
- Citation: Brunetto MR, Colombatto P, Bonino F. Bio-mathematical models of viral dynamics to tailor antiviral therapy in chronic viral hepatitis. World J Gastroenterol 2009; 15(5): 531-537
- URL: https://www.wjgnet.com/1007-9327/full/v15/i5/531.htm
- DOI: https://dx.doi.org/10.3748/wjg.15.531
The standardization and application in clinical practice of quantitative assays of nucleic acids enable us to measure the quantity of virus or viral load in the blood (viremia), and to study its fluctuations during treatment with antivirals in patients with chronic viral hepatitis. Since viremia represents the equilibrium between virus production by the infected cells and virus clearance by the antiviral reaction of the immune system or host’s antiviral immune response, viremia variations are the consequence of continuous alterations of the equilibrium between virus and host antiviral responses, which may vary during the natural course of the infection and are associated with the fluctuations of the liver disease activity[12]. However, the equilibrium between virus production and clearance can be artificially altered, which increases the clearance (removal) of circulating viruses (i.e. plasma-apheresis[3]), or reduces virus production with antiviral drugs. A rapid decline in viremia has been shown in patients with chronic human immunodeficiency viruses (HIV), hepatitis B virus (HBV) and hepatitis C virus (HCV) infections a few hours after administration of antivirals[4–6]. We may study the mechanisms responsible for these viral kinetics using mathematical models that can interpret viremia fluctuations according to hypotheses based on biological knowledge. The simulation of the complex biological phenomena by means of mathematical equations based only on suppositions, hypotheses or biological evidence has progressed consistently in several fields of medicine during the past few decades. Such modeling provides a simplified description of the biological process, but it maintains sufficient complexity to uncover the major determinants of the process itself, by studying the fluctuations of measured variables and predicted parameters with several simulations.
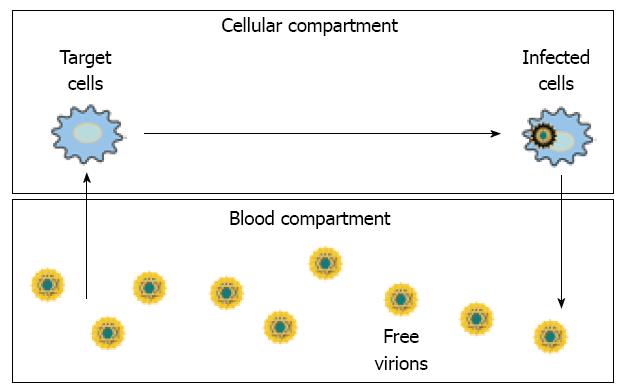
In chronic viral infections, standard models consider the existence of two separate but linked compartments: in the former, viruses replicate inside the infected cells, and in the latter, free virions circulate in the blood (Figure 1).
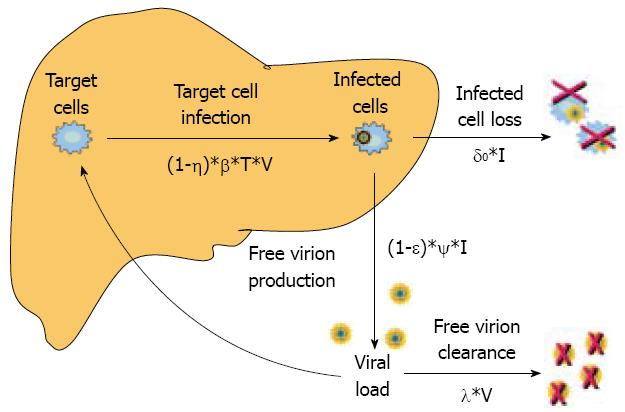
Dynamics and relations among uninfected target cells (T), infected cells (I) and viral load (V) are described by three different equations. Briefly, these models assume that target liver cells (T) replicate at rate s, die at rate d, and become infected (I) at a certain rate (βTV) proportional to both T and V when they encounter free virions circulating in the blood. The infected cells are eliminated at the rate of δ I and free virions, which are produced at the rate of Ψ I, are cleared at the rate of λ V. The parameters d, β, δ, Ψ, λ are the specific constant rates of formation and clearance of infected cells and circulating free virions. Antiviral therapy can reduce target-cell sensitivity to infection or the production rate of free virions that are released in the blood from the already infected cells. The former mechanism was assigned originally to interferon (IFN) in cell cultures[78], and the latter to drugs that block viral replication, such as nucleos(t)ide analogs or protease inhibitors[9].
In this model, the impact of antiviral drugs on the dynamics of viral infection is considered by the coefficients (1-η) and (1-epsilon) of the equations that describe the rate of target cell infection and free virion production, where η and epsilon represent the reduction in cell susceptibility to virus infection and the reduction in free virions production, respectively (Figure 2). It is understood that the time required by the drug to achieve complete antiviral efficacy is quite short and much shorter that the circulating virion half-life.
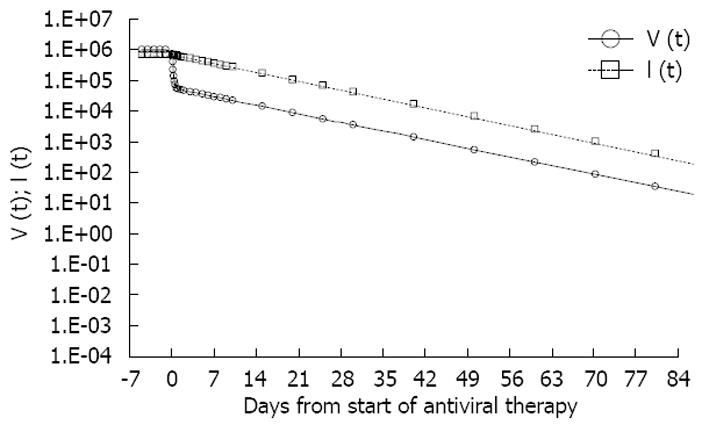
The standard model predicts that the pattern of viral load decline in patients treated with potent antivirals that block virus production is biphasic if the half-life of the circulating virions (T1/2 = ln2/λ) and that of the infected cells (T1/2 = ln2/δ) are different. The short half-life of the first phase of viral load decline suggests that it is associated with the clearance of circulating virions rather than infected cells (Figure 3).
Originally, Perelson et al[5], applying this approach to study HIV dynamics in patients treated with strong HIV-1 protease inhibitors, showed a very short half-life (nearly 6 h) of the virions in the blood and of infected cells (lymphocytes) (1.6 d)[5]. Likewise, when Neumann et al[6] used the same model approach in HCV-infected patients treated with IFN, they estimated that the virion half-life was 2.7 h. Moreover, contrary to HIV patients, they found that, just at the beginning of therapy, the estimated infected cell half-life (hepatocytes) was much longer (1.7-70 d), and was directly correlated with baseline viral load and inversely correlated with baseline alanine aminotransferase (ALT) levels.
With this analytical approach, the mechanism of IFN action in HCV patients is clear, and shows that the major antiviral effect is caused by a dose-dependent block of viral production in the infected cells. Therefore, the typical biphasic pattern of viral load decline observed in responder patients is to the result of a rapid reduction of free virion production, followed by a slower decrease in the number of infected cells. The modeling approach suggests monitoring the effectiveness of therapy individually, using the viral load, and predicting carefully the antiviral treatment outcome, in order to tailor the therapy schedule[910]. On the contrary, the standard models, although describing well the viral load decline in the first 2-4 wk of therapy, cannot adequately simulate the dynamics of the infection for the following period of treatment. Thus, the standard models, with the hypothesis of a constant clearance rate of the infected cells, provide an unrealistic estimation of time necessary to reach control or clearance of HBV/HCV infection.
To bypass this inconvenience, we have developed a multiphasic viral dynamics model in which we suppose a modulation of the immune system during therapy, according to negative feedback caused by a reduction in the number of infected cells. In addition, we utilized the ALT kinetics as a surrogate marker of infected-cell clearance. By this approach, we can compute the dynamics of infected cells during the whole treatment course, and we can find a good correlation between the infected cells number computed at the end of the therapy and the long term virological response in patients with chronic hepatitis C[1112].
Concerning HBV infection, in 1996, Nowak et al[13] applied the standard model to analyze the decrease in viral load in patients treated with lamivudine (LMV), the first drug to show strong antiviral action on hepatitis B e antigen (HBeAg)-positive chronic hepatitis B. LMV is able to reduce significantly new viral production by infected cells and inihibit viral reverse transcriptase (RT)/polymerase. During the first rapid phase of viral load decline until the second day of treatment, Nowak et al[13] estimated the virus decline constant rate (u) at 0.67/d, which corresponded to a half-life of nearly 1 d for free virions. Moreover, seeing the slowing down of viral load decline after a few days of treatment, the authors reached the conclusion that the drug might have blocked only partially virus production by infected cells. Thus, to show the partial efficacy of the drug, they introduced a new factor, ρ, defined as epsilon in following studies, and, to explain the second phase decline of the viral load, they hypothesized that this phase may be related to the decline in the number of infected cells. Accordingly, Nowak et al[13] estimated with different approaches the infected cell clearance rate, by comparing viral production rate before and after therapy, and by analyzing the decline in HBeAg, an HBV secretory protein that is produced continuously by infected cells during LMV therapy. By these two methods, it was estimated that the infected cells’ half-lives were equivalent and showed a wide range from 10 to 100 d (on average 16 d).
Another approach to the HBV model was implemented by Tsiang et al[14], who discarded the hypothesis that the number of infected cells is constant during therapy. They introduced the possibility that nucleos(t)ide analogs interfere with de novo infection of target hepatocytes since the RT/polymerase activity hampers the completion of the double-stranded DNA before migration towards the just-infected cell nucleous[15]. They have suggested that such an antiviral effect reduces the number of infected cells during treatment, and by this assumption, they were able to detail the HBV-DNA kinetics for 12 wk in patients treated with 30 mg/d adefovir (ADV)[14]. Using this model, Tsiang et al[14] have been able to show that the loss of infected hepatocytes is a rather slow process that can be described only from the second phase of viral load decline. They have reported half-lives for free virions and infected hepatocytes of 1.1 and 18 d, respectively, similar to those calcuated previously by Nowak et al[13].
Lewin et al[16], 2 years later, proposed instead a new model that suggests the possibility that infected cells can revert to their uninfected state after losing covalently closed circular DNA (cccDNA) by a non-cytolytic endogenous antiviral mechanism, similar to the one applied in the experimental models of acute HBV infection[17]. The authors have suggested that LMV or famciclovir (FCV) can partially inhibit new infections since cell polymerases in the hepatocytes nuclei can transform the circular HBV-DNA into cccDNA, which represents HBV matrix transcription. They have also found higher levels of variability in half-lives of free virions (from 1 to 92 h) and infected cells (from 2 to > 120 d). This variability is explained by the fact that even if most of the patients show a typical biphasic profile, the others show complex viral decline with “staircase” or multiphasic patterns.
Some of these patients, after the rapid first phase decline, had steady HBV-DNA levels for several days (even 4 wk) before viremia decreased, or in some cases, stabilized again. Variability in viremia decline may be explained by the patients’ heterogeneity according to their different conditions of HBV infection. In fact, a phase in which viremia remains stable may depend on a patient’s immunological condition, in which the infected cell clearance is very poor. This has been observed in patients at an early phase of HBV immune activation, which assumes a very low immune activation (very low δ) and a baseline number of infected cells approaching 100%. Wolters et al[18], following this interpretation, have
shown that higher baseline ALT levels are significantly associated with a greater rapidity of viral load decline in the second phase.
Different profiles of viremia decline may be caused by many reasons: modulation during therapy of cytolytic and non-cytolytic mechanisms of infected cell loss; presence of two or more infected cell populations with different half-lives; and infected cells with heterogeneity in their expression of drug-efflux pumps[16].
Lewin et al[16] have emphasized the complexity of HBV dynamics for treatments longer than a few weeks. Moreover, they have demonstrated the need for tight sampling immediately after drug administration, to warrant an accurate definition of viral clearance rate, and the need to evaluate the early stages of the delay before the drug starts its effect, as shown in HCV and HIV infections[5]. With tight viremia monitoring soon after the beginning of therapy (every 6 h in the first 2 d, compared to the 1-d interval adopted in previous studies), Wolters et al[18] have shown that the virion half-life is shorter (mean 15 h) than previously stated (24 h). These findings have been confirmed recently by other studies using higher sampling frequencies in the first 2 d of therapy (Table 1)[1920].
| Author | Therapy | HBeAg | Virion T1/2 (h) | Inf. cell T1/2 (d) | Antiviral effectiveness (%) |
| Nowak et al[13] | LMV 20-600 mg | POS | 24 | 10-100 | 87-99 |
| Lewin et al[16] | LMV 150 mg | POS | 28.5 | 2.4 > 120 | 95 |
| LMV + FCV | 99 | ||||
| Tsiang et al[14] | ADV | POS | 26.4 | 11-30 | 99 |
| Wolters et al[18] | LMV150 mg | POS | 131 | < 0-331 | 92-96 |
| Wolters et al[18] | ETV | POS/neg | 161 | 5.2-31.8 | 87-98 |
| Sypsa et al[19] | PegIFN2b 1-200 mg | neg | 12.71 | 2.7-75 | 83 |
| LMV 100 mg | 96 | ||||
| Colombatto et al[20] | PegIFN2a 180 mg | neg | nc | 2.5-77.3 | 88 |
| PegIFN2a + LMV | 8.21 | 4.7-33.3 | 99.6 (87) | ||
| LMV 100 mg | 9.51 | 4.3-56.5 | 99.4 (88) |
In one of these studies, Sypsa et al[19] analyzed HBV dynamics in HBeAg-negative patients during the first 4 wk of treatment with pegylated IFN-2b (PegIFN-2b) monotherapy or combined with LMV. The standard model was applied to patients receiving LMV alone or in combination, and accounted for the decreasing effectiveness of the drug between the weekly doses to patients treated with PegIFN-2b monotherapy. In this model, the impact of antiviral drugs on the dynamics of viral infection is considered by the terms (1-η) and (1-epsilon) of the equations 1, 2 and 3 (Figure 2), where η and epsilon represent the reduction in cell susceptibility to virus infection and the reduction in free virion production. This holds that the time required by the drug to achieve complete antiviral efficacy is quite short and much shorter than the circulating virion half-life. In this way, they could observe the fluctuations of viral load across the week of treatment in some patients, and this was ascribed to the decline of drug concentration between dosages. Besides the dependence of epsilon from the PegIFN 2b concentration, the authors suppose that the number of target and infected cells remain constant during the period of analysis (4 wk) and for the first 7 d of treatment. Starting from these assumptions, they emphasized that the mean antiviral efficacy of LMV monotherapy was superior to that of PegIFN-2b monotherapy (96.4% vs 82.6%) and comparable to that of PegIFN-2b + LMV (92.8%-94.4% for 100 &mgr;g or 200 &mgr;g, respectively). Moreover, they found that the infected cell half-life was comparable among the various groups of treatment (9.8 d vs 5.0 d vs 6.0 d for PegIFN-2b monotherapy, combination or LMV monotherapy, respectively), ranging from 2.7 to 75 d. Standard modeling of HBV dynamics was limited to the first 4-12 wk of therapy and was used to study direct antiviral activity of the drug. Instead, when using the model to tailor the treatment, it is mandatory to simulate viral dynamics throughout the whole treatment course, and this means introducing additional hypotheses about hepatocyte proliferation and immune system activity after the first month of therapy.
The hypothesis that the infected cell clearance activity by the immune system remains constant during therapy is in contrast with some common observations in HBV infection. For example, IgM anti-HBc levels, as surrogate markers of HBV-induced liver damage, decline progressively during treatment[12]. Thus, we have to hypothesize that the decrease in infected cells during treatment leads to a reduced immune stimulation that, in turn, could determine a decrease in the clearance of infected cells. It is likely that the kinetics of viral load decline during the first month of treatment are not simply biphasic in a significant proportion of patients treated either with LMV or PegIFNs + LMV. The average slope of weekly viral load declines observed by Sypsa et al[19] was similar during days 14-21 and 21-28 (-0.027 and 0.033 log10 cp/mL per day, respectively), but slower than those observed during days 7-14 (-0.067 log10 cp/mL per day).
These findings were ascribed to the prolonged first phase decline of viral load in some patients. In fact, we highlighted that all patients treated with LMV or Peg2a + LMV[20] had a viral load decline characterized by a rapid drop during the first phase of therapy (average HBV-DNA half-life of about 10 h during days 0-4), followed by another rapid drop (average HBV-DNA half-life of about 2 d) between days 4 and 14 (in particular between days 4-7). Attributing this second phase to the reduction in infected cells, according to the biphasic model, the infected cell half-life would be about 2 d only, and this would mean that chronic hepatitis patients with about 50% infected hepatocytes could lose > 10% of their overall hepatic mass every day. We could overcome this criticism if we suppose that the virion production in these patients was really inhibited in two phases: firstly a sharp drop as described in the model by the term “1-epsilon ”, followed by a second slower drop with exponential decline.
It is evident from all these studies that investigation of the long-term dynamics of HBV infection during the whole course of the antiviral therapy needs more specific models that take into account the complexity of HBV biology and its interplay with the host’s immune system. In consideration of the limitations previously described we developed a new model with simple biological assumptions on target and infected hepatocyte dynamics to make possible the simulation of the antiviral effects during the whole course of different antiviral treatments[20]. Briefly, the model holds that: (1) the sum of target and infected cells remains roughly constant and equals the total hepatocyte number in the normal liver (H0 = 2.5 × 1011 cells); (2) infected hepatocytes can generate infected daughter cells, as shown in animal models[21]; and (3) both target and infected cells contribute to the hepatocyte turnover in proportion to their relative numbers.
The following equation describes the full dynamics of the infected hepatocytes during therapy: dI(t)/dt = (1-η)β∙T(t)∙V(t) - δ(t)∙I(t)∙[1-I(t)/H0]. where η takes into account any variation of the susceptibility of target cells to get infected, as induced by therapy.
ALT serum levels as a marker of hepatocyte damage[22], as in other models[1123], were used to determine the infected hepatocyte number at baseline, according to the following equation: I0 = [ALT0-20]/[Φ∙δ0], where the numerical value of the constant Φ is equal to 3.24 × 10-4[11], calculated under the assumption that the normal ALT value is equal to 20 U/L and the natural hepatocyte turnover is 300/d[24].
The new model integrated the above hypothesis that the clearance rate of infected cells in HBeAg-negative chronic hepatitis patients could decrease after the first month of therapy because of the negative feedback derived from the progressive reduction of infected hepatocytes. Thus the equation describing the immune system activity was changed to: δ(t) = δ0∙[I(t-σ)/I0]k where σ is the time elapsing between the variation in the number of infected cells and the variation in the immune system activity (that is assumed to be 35 d), and k (which can vary from 0 to 1), which is the feedback parameter that links the variation in the virus-specific immune clearance activity to the variation in the number of infected cells. The multi-phase profile of the viral load decline observed in patients treated with LMV or Peg-IFNs + LMV during the first month of therapy led us to suggest that the free virus production might consist of two phases: the first one is described by the term 1-epsilon used in the standard model, and the second by an exponential function described by the following equation: Ψ(t) =(1-epsilon)∙[(1-γ)∙Ψ0∙e-φ∙t + γ∙Ψ0], where 1/φ represents the time constant of the second phase decline of virus production and (1-epsilon)γ∙Ψ0 is the asymptotic value (Ψasym) of the free virion production rate.
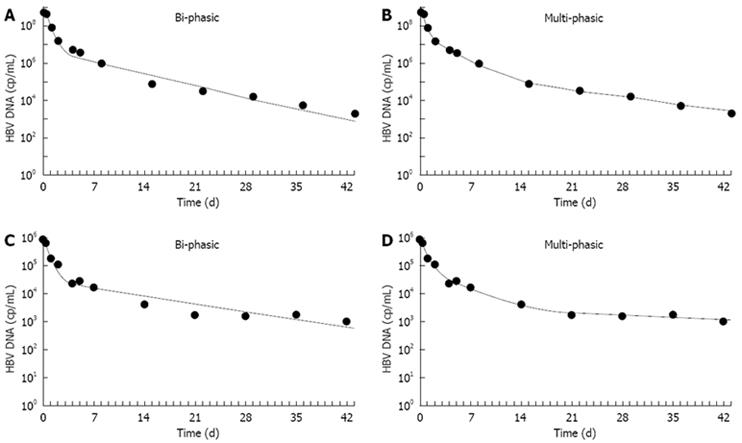
We then applied this multiphase model to 72 HBeAg-negative patients treated with LMV monotherapy and with Peg-IFN2a or with the two drugs combined in an international phase III study[25]. Applying the new model, we obtained a better fitting of the serum HBV-DNA multiphasic decline, as compared to the standard biphasic model (Figure 4), in 95% of the patients, and we could identify one additional phase of decline of viral production between days 4 and 14 in all LMV-treated patients.
We can hypothesize that two main biological mechanisms form the basis of this phase: a further reduction of virus production rate combined with an initial reduction in the number of infected cells. The additional antiviral effect of LMV inhibiting HBV replication during the second phase could be explained in several ways. One reason could be the decline of the cccDNA or viral minichromosome, provided that LMV blocks its production, as some authors have hypothesized in an animal model of hepadna-virus infection[26].
However, the half-lives determined for duck hepatitis B virus[26] and woodchuck hepatitis virus[21] in animal models and for HBV DNA in a chimpanzee experimental infection[27] were much longer than that computed for the above patients. Whalley et al[28] have reported an average HBV-DNA half-life of 3.7 ± 1.2 d compared with the 2 d found in the second phase of HBV-DNA decline during spontaneous resolution in patients with acute hepatitis B. Another hypothesis is that the block of virus production caused by LMV may restore some specific cytotoxic lymphocyte immune-mediated responses[29], and may also activate antiviral effects via cytokines, such as IFNγ and tumor necrosis factor α, which either reduce transcription or increase cccDNA degradation. It has been proven that such mechanisms inhibit HBV replication before hepatocellular damage in transgenic mice and chimpanzee acute hepatitis models[1722].
However, further studies are needed to understand better the biological reasons for this viral load decline. It is interesting to notice how Peg-IFN2a-treated patients had declines in serum HBV DNA much different from those observed in LMV-treated patients[20], given that the classic biphasic pattern was present during the first month of Peg-IFN2a monotherapy in the majority of patients. In the group of patients treated with Peg-IFN2a, however, the first slope of viral load decline was much lower than in the LMV-treated group with a mean HBV-DNA half-life of 1.6 ± 1.1 d and 9.5 ± 3.0 h, respectively.
The slower HBV-DNA decline during the first phase in patients treated with Peg-IFN2a monotherapy may have been caused by a decrease in virus production, similar to that induced by LMV with different kinetics, or to increased free virus clearance. Under the latter assumption, we noticed that the simulation of viral load decline did not fit with the experimental data, therefore, it appears more reasonable to accept the theory that Peg-IFN2a inhibits HBV replication inside the infected cells at a slower rate than LMV does.
The overall extent of inhibition of viral production induced by Peg-IFN2a was slightly higher (88%) than that reported by Sypsa et al[19] for Peg-IFN2b (82.6%). Such a difference emerged using our model, which allowed us to compute and study the antiviral effects of Peg-IFN during its whole period of action and not only during the first 4 d, as in the model of Sypsa et al[19].
Consistently, we could also prove that the extent of inhibition of viral production, in patients treated with LMV and Peg-IFN2a combination therapy, was comparable to that with LMV monotherapy, but the viral load decline was faster in the first phase (1/HBV-DNA decay constant: 2.79/d vs 1.91/d in LMV, P < 0.005) than in the second phase (1/HBV-DNA decay constant: 0.44 vs 0.34, P = 0.023).
In agreement with the fact that the molecular targets of LMV and IFN are different, these findings suggest that the mechanisms of IFN to inhibit HBV replication could be complementary and additive to those of LMV.
The experimental data reported in our study[20] proved also that the serum HBV-DNA decline after 4-5 wk of antiviral therapy tends to flatten in a large group of patients regardless of the treatment arm. If we assume that the viral load decline observed from day 14 onward depends uniquely on infected cell clearance, we can explain the slow decline in HBV-DNA levels after the first month of therapy, only accepting the reduction in the initial clearance rate of infected cells.
In the past, many efforts have been made to model variations in the immune response during viral infections[30], but they have led to a very complex system of differential equations without any effective result. Thus, with our model, we simply hypothesized a negative feedback on the immune clearance activity caused by a reduction in the number of infected cells, which is one major factor that induces cytotoxic immune responses.
The strength of the negative feedback, as modeled by the parameter “k”, was computed by fitting the HBV-DNA serum decline, which is usually detectable up to the third month of therapy. This allowed a more realistic simulation of the decline in HBV DNA and infected cells during the remaining period of therapy. It is noteworthy that, at the end of therapy, the mean logarithmic reduction in the HBV-infected hepatocyte fraction, computed by our model, was comparable in patients treated with Peg-IFN2a and LMV monotherapy (-3.30 log10 vs -3.31 log10, P > 0.05), but significantly higher in patients treated with combined Peg-IFN2a + LMV as compared to LMV monotherapy (-5.02 log10 vs -3.31 log10, P = 0.028).
These findings suggest that Peg-IFN2a, in spite of a lower inhibition of HBV replication, has an equivalent, if not higher, impact on infected cell clearance than that of viral polymerase inhibitors. This could be the direct consequence of PEG-IFN2a immunomodulatory activity that polymerase inhibitors are lacking.
Using our new multiphasic model, we could describe for the first time the second phase decrease in viral production that occurs mainly between days 4 and 14 in patients receiving LMV, alone or in combination.
Using the new model, we could prove that both IFN and LMV have inhibitory activities on HBV replication, but different kinetics. Their different mechanisms of action appear to work in synergy and cause faster declines in viral production during the first 2 wk of therapy in patients treated with both drugs.
The new model successfully describes the HBV infection dynamics far beyond the third month of antiviral therapy, under the assumption that the sum of infected and non-infected cells in HBeAg-negative chronic hepatitis B patients remains roughly constant during therapy, and both target and infected cells concur in hepatocyte turnover. These findings suggest that the ongoing production of new HBV-infected cells may occur after the division of already infected cells via transmission of the mini-chromosome-like cccDNA, when their immune-mediated clearance is reduced during long-term therapy. This might explain experimental data that report the persistence of high cccDNA levels even after 1 year of treatment with adefovir[31].
In the future, it will be very important to develop new models for a better simulation of HBV dynamics during various antiviral treatments, in order to predict the outcome of the infection after treatment discontinuation in every single patient, as is already available for hepatitis C patients[32]. The introduction of additional parameters that describe the HBV intrahepatic condition, related to infected hepatocytes and cccDNA copies, together with immune response markers in terms of immunoactivation and immunocompetence, could improve significantly the comprehension of the various profiles of response during and after antiviral treatment. In clinical practice, these new models could allow the development of simulators of treatment response that will be used as an “automatic pilot” for tailoring antiviral therapy in chronic hepatitis B, as well as chronic hepatitis C patients.
| 1. | Brunetto MR, Cerenzia MT, Oliveri F, Piantino P, Randone A, Calvo PL, Manzini P, Rocca G, Galli C, Bonino F. Monitoring the natural course and response to therapy of chronic hepatitis B with an automated semi-quantitative assay for IgM anti-HBc. J Hepatol. 1993;19:431-436. |
| 2. | Colloredo G, Bellati G, Leandro G, Colombatto P, Rho A, Bissoli F, Brunetto MR, Angeli G, Ideo G, Bonino F. Quantitative analysis of IgM anti-HBc in chronic hepatitis B patients using a new "gray-zone" for the evaluation of "borderline" values. J Hepatol. 1996;25:644-648. |
| 3. | Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, Mittler JE, Markowitz M, Moore JP, Perelson AS, Ho DD. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet. 1999;354:1782-1785. |
| 4. | Lam NP, Neumann AU, Gretch DR, Wiley TE, Perelson AS, Layden TJ. Dose-dependent acute clearance of hepatitis C genotype 1 virus with interferon alfa. Hepatology. 1997;26:226-231. |
| 5. | Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582-1586. |
| 6. | Neumann AU, Lam NP, Dahari H, Gretch DR, Wiley TE, Layden TJ, Perelson AS. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science. 1998;282:103-107. |
| 7. | Joklik WK. Interferons. Fields Virology. 2d ed. Raven Press: New York 1990; 383-410. |
| 8. | Gutterman JU. Cytokine therapeutics: lessons from interferon alpha. Proc Natl Acad Sci USA. 1994;91:1198-1205. |
| 9. | Layden JE, Layden TJ, Reddy KR, Levy-Drummer RS, Poulakos J, Neumann AU. First phase viral kinetic parameters as predictors of treatment response and their influence on the second phase viral decline. J Viral Hepat. 2002;9:340-345. |
| 10. | Zeuzem S, Pawlotsky JM, Lukasiewicz E, von Wagner M, Goulis I, Lurie Y, Gianfranco E, Vrolijk JM, Esteban JI, Hezode C. International, multicenter, randomized, controlled study comparing dynamically individualized versus standard treatment in patients with chronic hepatitis C. J Hepatol. 2005;43:250-257. |
| 11. | Colombatto P, Civitano L, Oliveri F, Coco B, Ciccorossi P, Flichman D, Campa M, Bonino F, Brunetto MR. Sustained response to interferon-ribavirin combination therapy predicted by a model of hepatitis C virus dynamics using both HCV RNA and alanine aminotransferase. Antivir Ther. 2003;8:519-530. |
| 12. | Perelson AS, Herrmann E, Micol F, Zeuzem S. New kinetic models for the hepatitis C virus. Hepatology. 2005;42:749-754. |
| 13. | Nowak MA, Bonhoeffer S, Hill AM, Boehme R, Thomas HC, McDade H. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci USA. 1996;93:4398-4402. |
| 14. | Tsiang M, Rooney JF, Toole JJ, Gibbs CS. Biphasic clearance kinetics of hepatitis B virus from patients during adefovir dipivoxil therapy. Hepatology. 1999;29:1863-1869. |
| 15. | Ganem D, Pollack JR, Tavis J. Hepatitis B virus reverse transcriptase and its many roles in hepadnaviral genomic replication. Infect Agents Dis. 1994;3:85-93. |
| 16. | Lewin SR, Ribeiro RM, Walters T, Lau GK, Bowden S, Locarnini S, Perelson AS. Analysis of hepatitis B viral load decline under potent therapy: complex decay profiles observed. Hepatology. 2001;34:1012-1020. |
| 17. | Guidotti LG, Rochford R, Chung J, Shapiro M, Purcell R, Chisari FV. Viral clearance without destruction of infected cells during acute HBV infection. Science. 1999;284:825-829. |
| 18. | Wolters LM, Hansen BE, Niesters HG, Levi-Drummer RS, Neumann AU, Schalm SW, de Man RA. The influence of baseline characteristics on viral dynamic parameters in chronic hepatitis B patients treated with lamivudine. J Hepatol. 2002;37:253-258. |
| 19. | Sypsa VA, Mimidis K, Tassopoulos NC, Chrysagis D, Vassiliadis T, Moulakakis A, Raptopoulou M, Haida C, Hatzakis A. A viral kinetic study using pegylated interferon alfa-2b and/or lamivudine in patients with chronic hepatitis B/HBeAg negative. Hepatology. 2005;42:77-85. |
| 20. | Colombatto P, Civitano L, Bizzarri R, Oliveri F, Choudhury S, Gieschke R, Bonino F, Brunetto MR. A multiphase model of the dynamics of HBV infection in HBeAg-negative patients during pegylated interferon-alpha2a, lamivudine and combination therapy. Antivir Ther. 2006;11:197-212. |
| 21. | Zhu Y, Yamamoto T, Cullen J, Saputelli J, Aldrich CE, Miller DS, Litwin S, Furman PA, Jilbert AR, Mason WS. Kinetics of hepadnavirus loss from the liver during inhibition of viral DNA synthesis. J Virol. 2001;75:311-322. |
| 22. | Ribeiro RM, Layden-Almer J, Powers KA, Layden TJ, Perelson AS. Dynamics of alanine aminotransferase during hepatitis C virus treatment. Hepatology. 2003;38:509-517. |
| 23. | Murray JM, Wieland SF, Purcell RH, Chisari FV. Dynamics of hepatitis B virus clearance in chimpanzees. Proc Natl Acad Sci USA. 2005;102:17780-17785. |
| 24. | Mac Sween RNM, Antony PP, Scheuer PJ. Pathology of the liver. Churchill Livingstone: Edinburgh 1987; 635-667. |
| 25. | Marcellin P, Lau GK, Bonino F, Farci P, Hadziyannis S, Jin R, Lu ZM, Piratvisuth T, Germanidis G, Yurdaydin C. Peginterferon alfa-2a alone, lamivudine alone, and the two in combination in patients with HBeAg-negative chronic hepatitis B. N Engl J Med. 2004;351:1206-1217. |
| 26. | Addison WR, Walters KA, Wong WW, Wilson JS, Madej D, Jewell LD, Tyrrell DL. Half-life of the duck hepatitis B virus covalently closed circular DNA pool in vivo following inhibition of viral replication. J Virol. 2002;76:6356-6363. |
| 27. | Wieland SF, Spangenberg HC, Thimme R, Purcell RH, Chisari FV. Expansion and contraction of the hepatitis B virus transcriptional template in infected chimpanzees. Proc Natl Acad Sci USA. 2004;101:2129-2134. |
| 28. | Whalley SA, Murray JM, Brown D, Webster GJ, Emery VC, Dusheiko GM, Perelson AS. Kinetics of acute hepatitis B virus infection in humans. J Exp Med. 2001;193:847-854. |
| 29. | Boni C, Penna A, Ogg GS, Bertoletti A, Pilli M, Cavallo C, Cavalli A, Urbani S, Boehme R, Panebianco R. Lamivudine treatment can overcome cytotoxic T-cell hyporesponsiveness in chronic hepatitis B: new perspectives for immune therapy. Hepatology. 2001;33:963-971. |
| 30. | Marchuk GI. Mathematical modelling of immune response in infectious diseases. Kluwer Academic: Dordrecht 1997; 225-230. |
| 31. | Werle-Lapostolle B, Bowden S, Locarnini S, Wursthorn K, Petersen J, Lau G, Trepo C, Marcellin P, Goodman Z, Delaney WE 4th. Persistence of cccDNA during the natural history of chronic hepatitis B and decline during adefovir dipivoxil therapy. Gastroenterology. 2004;126:1750-1758. |
| 32. | Colombatto P, Ciccorossi P, Maina AM, Civitano L, Oliveri F, Coco B, Romagnoli V, Bonino F, Brunetto MR. Early and accurate prediction of Peg-IFNs/ribavirin therapy outcome in the individual patient with chronic hepatitis C by modeling the dynamics of the infected cells. Clin Pharmacol Ther. 2008;84:212-215. |