Published online Dec 21, 2006. doi: 10.3748/wjg.v12.i47.7660
Revised: November 1, 2006
Accepted: November 6, 2006
Published online: December 21, 2006
AIM: To assess the sampling variability of computer-aided, fractal-corrected measures of fibrosis in liver biopsies.
METHODS: Samples were derived from six to eight different parts of livers removed from 12 patients with clinically and histologically proven cirrhosis undergoing orthotopic liver transplantation. Sirius red-stained sections with a thickness of 2 μm were digitized using a computer-aided image analysis system that automatically measures the surface of fibrosis, as well as its outline perimeter, fractal surface and outline dimensions, wrinkledness, and Hurst coefficient.
RESULTS: We found a high degree of inter-sample variability in the measurements of the surface [coefficient of variation (CV) = 43% ± 13%] and wrinkledness (CV = 28% ± 9%) of fibrosis, but the inter-sample variability of Hurst’s exponent was low (CV = 14% ± 2%).
CONCLUSION: This study suggests that Hurst’s exponent might be used in clinical practice as the best histological estimate of fibrosis in the whole organ, and evidences the fact that biopsy sections, which are fundamental for the qualitative diagnosis of chronic hepatitis, play a key role in the quantitative estimate of architectural changes in liver tissue.
- Citation: Grizzi F, Russo C, Franceschini B, Rocco MD, Torri V, Morenghi E, Fassati LR, Dioguardi N. Sampling variability of computer-aided fractal-corrected measures of liver fibrosis in needle biopsy specimens. World J Gastroenterol 2006; 12(47): 7660-7665
- URL: https://www.wjgnet.com/1007-9327/full/v12/i47/7660.htm
- DOI: https://dx.doi.org/10.3748/wjg.v12.i47.7660
The discovery of specific antiviral and antifibrotic treatments and the current debate concerning the possibility of reversing liver fibrosis[1-5] emphasize the need for rigorous quantitative methods capable of detecting small differences in the liver extra-cellular matrix (ECM). Such methods should provide, on the basis of biopsy section analysis, a representative index of the status of the whole organ.
Although the use of a panel of biochemical markers or other non-invasive approaches has been proposed[5-13], liver biopsy remains the “reference standard” for confirming a clinical diagnosis of chronic hepatitis, assessing disease severity, and monitoring the efficacy of therapeutic interventions[14-17].
All of the semi-quantitative systems for defining the histological stage of chronic liver disease[18-21] have been extensively criticized because their scores generate ordinals to label subjective categories of severity that are inevitably influenced by the skill and experience of the observer[22-24]. In addition, these ordinals are not continuous variables because the absolute distances between the labeled categories are unknown, restricting their application to the most widely used methods of mathematical and statistical analyses[25,26].
Available quantitative morphometric methods[27-29] have all the primary defects in their use of the Euclidean geometry, which is inexact to describe irregular objects, and the international system (IS) meter which is unsuitable for measuring highly irregular objects.
To investigate the dynamics underlying chronic hepatitis we have recently developed a computer-aided method based on the principles of fractal geometry that automatically measures some of the geometric characteristics of the irregularly shaped collagen fragments making up liver fibrosis[30-33]. However, in applying this quantitative method, we reflected upon the patchy (irregularly shaped or considered fractal) deposition of ECM components (Figure 1). Thus, we decided to revisit previous investigations that focused on evaluating whether a biopsy section reflects the fibrotic status of the whole liver[34-41].
We have studied biopsy sections of liver samples derived from patients undergoing orthotopic liver transplantation (OLT) with clinically and histologically proven cirrhosis. We used these samples to assess the degree of sampling variability of the quantitative fractal geometric parameters of liver fibrosis.
We found a high degree of inter-sample variability in the measurements of the surface and wrinkledness of fibrosis, but a low variability of Hurst’s exponent, which gives a measure of the heterogeneous distribution of a set of irregularly-shaped objects. With the support of the Euclidean and fractal dimensions, it is capable of evaluating the loss of natural order occurring in the histological picture as a result of the disruption of the natural quantitative relationship between the metric spaces covered by fibrosis and the parenchyma[42]. This gives the alterations in the significance of a physical variable and makes Hurst’s exponent the descriptor of the configurational disorder of hepatic tissue.
The study was conducted in accordance with the guidelines of the Ethics Committee of the Ospedale Maggiore IRCCS (Milan, Italy), where patients were treated.
The study was carried out on livers removed from 12 patients with clinically and histologically proven cirrhosis during OLT in order to define the variability of measured parameters in multiple specimens sampled in different sites of each liver’s mass. From each liver, 6 to 8 biopsy specimens (> 10 mm in length) were collected and analyzed. All patients were positive for hepatitis C virus (HCV) infection.
Two consecutive 2 μm-thick sections were cut from each formalin-fixed, paraffin-embedded specimen. One was subsequently stained with hematoxylin-eosin solution, and the other was stained with a freshly prepared Sirius red collagen staining solution[43].
The sections were independently staged by two expert hepatopathologists using Knodell’s histology activity index (HAI)[18], and the Sheuer[19], Ishak[20] and METAVIR[21] semi-quantitative scoring systems.
For image analysis the Sirius red-stained sections were digitized at 20 × objective magnification by using a Leica DMLA microscope (Leica, Italy) equipped with an x-y translator table, a digital camera (Leica DC200, Leica, Italy), and an Intel Dual-Pentium III, 660 MHz computer with incorporated ad hoc image analysis software. This software automatically selects fibrosis on the basis of RGB color segmentation[32-33]. The same image intensity level was used throughout the study. The surface area and perimeter of the fibrosis, together with its fractal surface and outline dimensions, wrinkledness, and Hurst exponent, were automatically calculated for each digitized histological section as previously described[33]. The entire procedure (patent pending) was very speedy as it digitized and furnished 11 parameters concerning the physical state of fibrosis in 10 s/mm2 of tissue biopsy surface. In brief, we geometrically defined the following:
(a) Fibrosis as a set of irregularly shaped objects (collagen fragments or islets) that could be distinguished from the remaining tissue by their chemical affinity to Sirius red dye (Figure 1A).
(b) Area of fibrosis as the sum of the areas of the collagen islets (Figure 1B), expressed as a percentage of the true liver biopsy section surface area excluding any unfilled natural spaces (vascular and biliary cavities, and sinusoidal spaces) and tissue-free spaces resulting from specimen manipulation. As collagen islets are irregularly shaped, the measures of their surface areas and outline perimeters were automatically corrected by using a fractal-reference meter[32]. The fractal-rectified fibrosis surface area (AF) is given by the formula:
AF ≌ AM + λΑ (D - Dγ) (AB - AM) (1)
where AM is the morphometric area of fibrosis, D the fractal surface dimension, Dγ the Euclidean dimension, AB the liver biopsy section surface area, (AB - AM) the area of the remaining tissue, and [λΑ (∆ - ∆γ)] the probability factor. λΑ was found to be ≌ 0.01[32,33]. Equation (1) also makes it possible to consider the smallest “probably present” collagen islets (which were invisible at the magnification used in the study)[32,33] in the measurement process.
(c) Fractal-rectified length of the perimeter of fibrosis (PF) as the sum of the lengths of the perimeters of each collagen islet (Figure 1B) given by the formula:
PF ≌ PM [1 + λP (D − Dγ) ] (2)
where PM is the morphometric perimeter of fibrosis, λP is the dilation constant for the perimeter of the collagen islets depending only on the scale of observation[32,33], and was found to be ≌ 4.5[32,33]. The obtained PF values were subsequently used to determine the wrinkledness of the fibrosis.
(d) Fractal surface and outline dimensions of fibrosis as measures of its space-filling properties (Figure 1C), which were automatically estimated by means of the box-counting method using the formula (3) (Figure 2):
where DB is the box-counting fractal dimension, ε the side length of the box, and N(ε) the smallest number of boxes of side ε required to cover the complete surface or the outline of the object (Figure 1D). As the zero limit cannot be applied to biological objects, the dimensions were calculated as D = d, where d is the slope of the graph of log [N(ε)] against log 1/ε. The log-log graphs were plotted, the linear segments were identified using least squares regression, and their gradients were calculated using an iterative resistant line method[30-33,44-46].
(e) Wrinkledness (W) of fibrosis as a form-factor, given by the formula (4) (Figure 3):
where R is the roundness coefficient[32,33].
(f) Hurst exponent of fibrosis as a measure of the heterogeneous distribution of a set of irregularly-shaped objects (in this case, collagen islets), obtained using the relationship:
H = Dγ + 1 – D (5)
where D is the fractal dimension of the outline of all of the collagen islets making up the fibrosis[33,47-49].
All data are expressed as mean ± SD and were analyzed using Statistica software (StatSoft Inc., Tulsa, OK, USA).
The sampling variability of the fibrosis surface, wrinkledness, and Hurst exponent was evaluated in each liver by using the coefficient of variation (CV) given by the formula:
CV=(SD/mean)×100% (6)
The obtained data were analyzed using the Student t-test. P values of less than 0.05 were considered statistically significant.
All histological sections were staged as cirrhosis and classified in the maximum category of each of the 4 systems used in the study (HAI, and the Scheuer, Ishak and METAVIR scoring systems).
Table 1 shows the fractal morphometric measures of each investigated liver. The minimum and maximum values of AF obtained by measuring the 88 biopsy sections were 4.95% and 55.67% of the specimen area, with a mean value of 20.46% ± 10.55%.
| Liver | Sections (n) | AF (%) | PF (μm) | D | W | H | |
| DA | DP | ||||||
| 1 | 6 | 19.17 ± 10.98 (9.1-38.4) | 6964.74 ± 3128.95 (4646.2-12328.6) | 1.64 ± 0.06 (1.6-1.8) | 1.56 ± 0.06 (1.5-1.7) | 1178.82 ± 198.79 (897.9-1453.3) | 0.35 ± 0.06 (0.3-0.5) |
| 2 | 8 | 22.00 ± 7.99 (8.5-35.1) | 3570.14 ± 1170.41 (1365.9-5240.7) | 1.66 ± 0 06 (1.5-1.7) | 1.57 ± 0.06 (1.4-1.7) | 748.94 ± 129.68 (1365.9-5240.7) | 0.34 ± 0.06 (0.4-0.6) |
| 3 | 8 | 15.62 ± 8.73 (5.5-33.8) | 4673.66 ± 4405.36 (907.6-15037.6) | 1.62 ± 0.07 (1.5-1.8) | 1.55 ± 0.07 (1.4-1.7) | 881.40 ± 354.46 (460-1641) | 0.37 ± 0.07 (0.3-0.6) |
| 4 | 8 | 32.83 ± 6.35 (25-44.2) | 7727.38 ± 4215.44 (2949.9-16341.1) | 1.74 ± 0.04 (1.6-1.8) | 1.64 ± 0.04 (1.6-1.7) | 1103.06 ± 307.68 (701.7-1649.3) | 0.26 ± 0.04 (0.3-0.4) |
| 5 | 6 | 19.53 ± 11.06 (4.95-32.9) | 6833.67 ± 3057.82 (3057.8-11213.4) | 1.64 ± 0.07 (1.5-1.7) | 1.56 ± 0.06 (1.5-1.6) | 1172.91 ± 342.08 (666.1-1690.3) | 0.35 ± 0.07 (0.4-0.5) |
| 6 | 8 | 31.42 ± 15.22 (13.1-55.67) | 7035.59 ± 3871.56 (2290.7-14153.6) | 1.74 ± 0.07 (1.6-1.8) | 1.66 ± 0.06 (1.6-1.8) | 1155.17 ± 367.12 (793.7-1713.5) | 0.25 ± 0.04 (0.2-0.4) |
| 7 | 6 | 12.81 ± 5.26 (6.5-20.8) | 6576.58 ± 4024.44 (2626.9-12294.2) | 1.61 ± 0.05 (1.5-1.7) | 1.55 ± 0.05 (1.5-1.6) | 1121.75 ± 429.47 (717.8-1796) | 0.38 ± 0.07 (0.4-0.5) |
| 8 | 6 | 13.52 ± 6.09 (5.5-21.7) | 5224.22 ± 3583.102 (1599.6-11107.4) | 1.57 ± 0.07 (1.5-1.7) | 1.49 ± 0.07 (1.4-1.6) | 908.53 ± 363.51 (547.1-1363.4) | 0.42 ± 0.07 (0.4-0.6) |
| 9 | 8 | 12.34 ± 6.87 (6.7-23.9) | 5087.80 ± 1619.29 (3081.7-6801.2) | 1.62 ± 0.05 (1.6-1.7) | 1.55 ± 0.05 (1.5-1.6) | 1076.95 ± 15.20 (902.5-1328.3) | 0.37 ± 0.05 (0.4-0.5) |
| 10 | 8 | 18.87 ± 5.54 (9.8-25) | 8133.72 ± 3459.80 (2699.6-12552.2) | 1.68 ± 0.05 (1.6-1.8) | 1.61 ± 0.06 (1.5-1.7) | 1276.35 ± 421.98 (635.9-1834.8) | 0.31 ± 0.05 (0.3-0.5) |
| 11 | 8 | 18.74 ± 4.93 (9.7-25.2) | 5760.81 ± 1698.43 (2602.6-7805.2) | 1.63 ± 0.05 (1.6-1.7) | 1.56 ± 0.05 (1.5-1.6) | 958.96 ± 173.98 (632.4-1147.6) | 0.34 ± 0.05 (0.4-0.5) |
| 12 | 8 | 25.26 ± 11.35 (9.7-44.4) | 5621.00 ± 2603.91 (1637.6-9839.8) | 1.71 ± 0.06 (1.6-1.8) | 1.62 ± 0.05 (1.5-1.7) | 970.14 ± 255.81 (609.3-1455.8) | 0.28 ± 0.06 (0.3-0.5) |
The same 88 biopsy sections gave PF values ranging from 907.6 μm and 16341.1 μm, with a mean value of 6073.6 ± 3299.6 μm.
The values of the fractal surface dimension of fibrosis ranged from 1.47 to 1.84 (mean 1.66 ± 0.07), and those of the fractal outline dimension ranged from 1.41 to 1.77, with a mean of 1.58 ± 0.07.
The mean W value was 1041.6 ± 321.25 (range: 460-1834.8). The H values ranged from 0.23 to 0.59, with a mean of 0.41 ± 0.07.
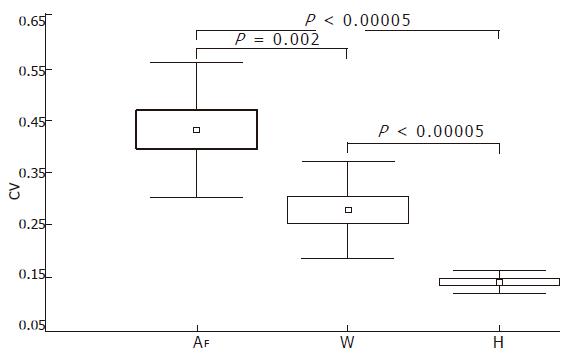
Table 2 shows the inter-sample variability determined in the 6 to 8 biopsy samples that were taken from each of the 12 livers. High CV values were obtained for both the surface (CV = 43% ± 12%, range, 19.79-57.28) and the wrinkledness of fibrosis (CV = 28% ± 9%, range, 14.13-40.22), whereas the variability of Hurst’s exponent was low (CV = 14% ± 2%, range, 10.71-17.74). Statistical comparisons of the mean surface, wrinkledness, and Hurst’s exponent CVs showed that Hurst exponent was characterized by a smaller range and that Hurst exponent mean CV was statistically different from that of the fibrosis surface (P < 0.00005) and wrinkledness (P < 0.00005) (Figure 4).
| CV (%) | ||||
| Patient | Sections (n) | AF | W | H |
| 1 | 6 | 57.28 | 16.86 | 13.90 |
| 2 | 8 | 36.31 | 17.31 | 15.27 |
| 3 | 8 | 55.9 | 40.22 | 16.86 |
| 4 | 8 | 19.79 | 27.89 | 10.71 |
| 5 | 6 | 56.64 | 29.17 | 14.87 |
| 6 | 8 | 48.44 | 31.78 | 17.74 |
| 7 | 6 | 41.05 | 38.29 | 11.67 |
| 8 | 6 | 45.05 | 40.01 | 15.41 |
| 9 | 8 | 55.67 | 14.13 | 11.45 |
| 10 | 8 | 29.38 | 33.06 | 16.13 |
| 11 | 8 | 26.31 | 18.14 | 12.68 |
| 12 | 8 | 44.94 | 26.37 | 15.13 |
During the course of chronic hepatitis, the net result of the balance between ECM synthesis (fibrogenesis) and degradation (fibrolysis) is the irregular shape and patchy distribution of collagen fragments. Currently, the lack of robust and representative markers of fibrosis is the single greatest factor limiting both the validation of progression or regression of fibrosis, and the testing of antifibrotic therapies in clinical trials. This observation prompted us to investigate whether fractal-rectified measures of fibrosis recognized in two-dimensional liver biopsy sections provide concrete scalars that can represent the state of the whole organ. This aim was reinforced by recent proposals to use methods of analyzing blood stream molecules as a means of scoring liver fibrosis. However, none of these methods has inspired sufficient confidence to displace our reliance on hepatic histology[33,50-57].
To obtain rigorous measures of irregularly shaped collagen islets, a computer-aided method was developed that uses a fractal-corrected meter to provide close-to-reality measurements[30-33]. Such measurements cannot be obtained using the Euclidean meter, which is able to quantify only smooth objects (e.g. geometrical figures) that are practically unknown in Nature[30-33,44-46].
To determine the extent to which a histological section represents the whole liver we compared the scalar number generated by our quantitative method representing the magnitude of the area, wrinkledness and Hurst’s exponent of the fibrosis recognized in two-dimensional sections taken from different parts of 12 explanted livers. The present study was restricted to explanted cirrhotic livers as they could make it possible to sample multiple specimens from the same liver, but impossible to obtain from the liver of living patients.
In a previous study, we found a high degree of intra-sample variability in the surface area of fibrosis that revealed the three-dimensional spatial irregularity of fibrosis detectable in the sample that reveals the non-representativity of the sample respect in the whole liver tissue[33]. In line with this finding, our analysis of the surface area (CV = 43% ± 12%) and wrinkledness (CV = 28% ± 9%) of the fibrosis detected in two-dimensional sections (Table 2) taken from multiple biopsies excised in different sites of each liver mass, revealed a high degree of variability and thus a low possibility to predict the state of a sample and that of the whole organ (i.e. liver).
Chronic hepatitis is an irregular dynamical process complex both in time and in space, and its end stage known as cirrhosis is characterized by a wide distortion of the normal parenchyma configuration and secondary vascular events that might contribute to the heterogeneous distribution of ECM components[58].
The lowest variability (CV = 14% ± 2%) was detected for Hurst exponent in our study. We have introduced this parameter to measure the loss of natural liver tissue harmony[33]. This concept results from the ratio of two quantitative canons normally found in disease-free livers: 2% of ECM belonging to the bearing system of the liver tissue, and 98% of parenchymal tissue.
Hurst’s exponent which gives a measure of the heterogeneous distribution of a set of irregularly-shaped objects, is capable of evaluating the loss of natural order that occurs in the histological picture as a result of the disruption of the natural quantitative relationship between the metric spaces covered by fibrosis and the parenchyma[42]. This is because Hurst exponent derives from the interaction between the Euclidean and fractal dimensions, becoming a measure unit. Both Euclidean and fractal dimensions separately express only the position of an object in the Euclidean space.
The present results suggest that this quantitative parameter might be more useful in clinical practice as a means of estimating fibrosis and its progression or reversibility after therapy, than the surface and wrinkledness of fibrosis.
Our results also underscore the key role of biopsy analyses both in diagnosing the histology of chronic hepatitis and in quantifying changes in the geometry of ECM islets. The clinical relevance of any of the parameters issued from morphometry is however not known yet. This incompleteness may be due to the low rigor in the actual detection of the data based on the Euclidean geometry and the use of linear IS meter to measure very irregular objects[30-33].
In summary, our method offers the following theoretical and experimental contributions. Hurst’s exponent can be used to provide a good estimate of tissue alterations. Objective and rigorous metric measures of the fibrosis of a section of biopsied tissue do not fully represent the status of the organ as a whole. Hurst’s exponent of liver tissue in a histological section is a good descriptor of the architectural condition of the whole liver.
Hurst’s exponent therefore gives scientific value to the liver tissue status indicated by the term of architectural change, originally used by Ishak et al[20] in their definition of the staging of chronic viral hepatitis.
S- Editor Liu Y L- Editor Wang XL E- Editor Lu W
| 1. | Bonis PA, Friedman SL, Kaplan MM. Is liver fibrosis reversible. N Engl J Med. 2001;344:452-454. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 129] [Cited by in RCA: 129] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 2. | Desmet VJ, Roskams T. Cirrhosis reversal: a duel between dogma and myth. J Hepatol. 2004;40:860-867. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 172] [Cited by in RCA: 168] [Article Influence: 8.0] [Reference Citation Analysis (0)] |
| 3. | Fallowfield JA, Iredale JP. Reversal of liver fibrosis and cirrhosis--an emerging reality. Scott Med J. 2004;49:3-6. [PubMed] |
| 4. | Pol S, Carnot F, Nalpas B, Lagneau JL, Fontaine H, Serpaggi J, Serfaty L, Bedossa P, Bréchot C. Reversibility of hepatitis C virus-related cirrhosis. Hum Pathol. 2004;35:107-112. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 109] [Cited by in RCA: 93] [Article Influence: 4.4] [Reference Citation Analysis (0)] |
| 5. | Desmet VJ. Comments on cirrhosis reversal. Dig Liver Dis. 2005;37:909-916. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 21] [Cited by in RCA: 21] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 6. | Poynard T, Imbert-Bismut F, Munteanu M, Messous D, Myers RP, Thabut D, Ratziu V, Mercadier A, Benhamou Y, Hainque B. Overview of the diagnostic value of biochemical markers of liver fibrosis (FibroTest, HCV FibroSure) and necrosis (ActiTest) in patients with chronic hepatitis C. Comp Hepatol. 2004;3:8. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 250] [Cited by in RCA: 280] [Article Influence: 13.3] [Reference Citation Analysis (0)] |
| 7. | Callewaert N, Van Vlierberghe H, Van Hecke A, Laroy W, Delanghe J, Contreras R. Noninvasive diagnosis of liver cirrhosis using DNA sequencer-based total serum protein glycomics. Nat Med. 2004;10:429-434. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 336] [Cited by in RCA: 322] [Article Influence: 15.3] [Reference Citation Analysis (0)] |
| 8. | Ziol M, Handra-Luca A, Kettaneh A, Christidis C, Mal F, Kazemi F, de Lédinghen V, Marcellin P, Dhumeaux D, Trinchet JC. Noninvasive assessment of liver fibrosis by measurement of stiffness in patients with chronic hepatitis C. Hepatology. 2005;41:48-54. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1090] [Cited by in RCA: 1095] [Article Influence: 54.8] [Reference Citation Analysis (0)] |
| 9. | Sud A, Hui JM, Farrell GC, Bandara P, Kench JG, Fung C, Lin R, Samarasinghe D, Liddle C, McCaughan GW. Improved prediction of fibrosis in chronic hepatitis C using measures of insulin resistance in a probability index. Hepatology. 2004;39:1239-1247. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 138] [Cited by in RCA: 133] [Article Influence: 6.3] [Reference Citation Analysis (0)] |
| 10. | Rosenberg WM, Voelker M, Thiel R, Becka M, Burt A, Schuppan D, Hubscher S, Roskams T, Pinzani M, Arthur MJ. Serum markers detect the presence of liver fibrosis: a cohort study. Gastroenterology. 2004;127:1704-1713. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 756] [Cited by in RCA: 759] [Article Influence: 36.1] [Reference Citation Analysis (0)] |
| 11. | Patel K, Gordon SC, Jacobson I, Hézode C, Oh E, Smith KM, Pawlotsky JM, McHutchison JG. Evaluation of a panel of non-invasive serum markers to differentiate mild from moderate-to-advanced liver fibrosis in chronic hepatitis C patients. J Hepatol. 2004;41:935-942. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 242] [Cited by in RCA: 241] [Article Influence: 11.5] [Reference Citation Analysis (0)] |
| 12. | Imbert-Bismut F, Ratziu V, Pieroni L, Charlotte F, Benhamou Y, Poynard T. Biochemical markers of liver fibrosis in patients with hepatitis C virus infection: a prospective study. Lancet. 2001;357:1069-1075. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1066] [Cited by in RCA: 1037] [Article Influence: 43.2] [Reference Citation Analysis (0)] |
| 13. | Yamada H, Ebara M, Yamaguchi T, Okabe S, Fukuda H, Yoshikawa M, Kishimoto T, Matsubara H, Hachiya H, Ishikura H. A pilot approach for quantitative assessment of liver fibrosis using ultrasound: preliminary results in 79 cases. J Hepatol. 2006;44:68-75. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 60] [Cited by in RCA: 43] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 14. | Desmet VJ. Liver tissue examination. J Hepatol. 2003;39 Suppl 1:S43-S49. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 25] [Cited by in RCA: 19] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 15. | Bravo AA, Sheth SG, Chopra S. Liver biopsy. N Engl J Med. 2001;344:495-500. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1843] [Cited by in RCA: 1736] [Article Influence: 72.3] [Reference Citation Analysis (0)] |
| 16. | Kleiner DE. The liver biopsy in chronic hepatitis C: a view from the other side of the microscope. Semin Liver Dis. 2005;25:52-64. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 50] [Cited by in RCA: 45] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 17. | Desmet V, Fevery J. Liver biopsy. Baillieres Clin Gastroenterol. 1995;9:811-828. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 10] [Cited by in RCA: 9] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 18. | Desmet VJ. Knodell RG, Ishak KG, Black WC, Chen TS, Craig R, Kaplowitz N, Kiernan TW, Wollman J. Formulation and application of a numerical scoring system for assessing histological activity in asymptomatic chronic active hepatitis [Hepatology 1981; 1: 431-435]. J Hepatol. 2003;38:382-386. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2558] [Cited by in RCA: 2507] [Article Influence: 57.0] [Reference Citation Analysis (0)] |
| 19. | Scheuer PJ. Classification of chronic viral hepatitis: a need for reassessment. J Hepatol. 1991;13:372-374. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1130] [Cited by in RCA: 1198] [Article Influence: 35.2] [Reference Citation Analysis (0)] |
| 20. | Ishak K, Baptista A, Bianchi L, Callea F, De Groote J, Gudat F, Denk H, Desmet V, Korb G, MacSween RN. Histological grading and staging of chronic hepatitis. J Hepatol. 1995;22:696-699. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 3521] [Cited by in RCA: 3782] [Article Influence: 126.1] [Reference Citation Analysis (1)] |
| 21. | Bedossa P, Poynard T. An algorithm for the grading of activity in chronic hepatitis C. The METAVIR Cooperative Study Group. Hepatology. 1996;24:289-293. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2860] [Cited by in RCA: 3082] [Article Influence: 106.3] [Reference Citation Analysis (0)] |
| 22. | Hübscher SG. Histological grading and staging in chronic hepatitis: clinical applications and problems. J Hepatol. 1998;29:1015-1022. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 70] [Cited by in RCA: 62] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 23. | Scheuer PJ. Assessment of liver biopsies in chronic hepatitis: how is it best done. J Hepatol. 2003;38:240-242. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 13] [Cited by in RCA: 9] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 24. | Rosenberg WM. Rating fibrosis progression in chronic liver diseases. J Hepatol. 2003;38:357-360. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 31] [Cited by in RCA: 31] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 25. | Lagging LM, Westin J, Svensson E, Aires N, Dhillon AP, Lindh M, Wejstål R, Norkrans G. Progression of fibrosis in untreated patients with hepatitis C virus infection. Liver. 2002;22:136-144. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 58] [Cited by in RCA: 51] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 26. | Svensson E. Ordinal invariant measures for individual and group changes in ordered categorical data. Stat Med. 1998;17:2923-2936. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 2] [Reference Citation Analysis (0)] |
| 27. | Masseroli M, Caballero T, O'Valle F, Del Moral RM, Pérez-Milena A, Del Moral RG. Automatic quantification of liver fibrosis: design and validation of a new image analysis method: comparison with semi-quantitative indexes of fibrosis. J Hepatol. 2000;32:453-464. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 99] [Cited by in RCA: 93] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 28. | Pilette C, Rousselet MC, Bedossa P, Chappard D, Oberti F, Rifflet H, Maïga MY, Gallois Y, Calès P. Histopathological evaluation of liver fibrosis: quantitative image analysis vs semi-quantitative scores. Comparison with serum markers. J Hepatol. 1998;28:439-446. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 154] [Cited by in RCA: 147] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 29. | Wright M, Thursz M, Pullen R, Thomas H, Goldin R. Quantitative versus morphological assessment of liver fibrosis: semi-quantitative scores are more robust than digital image fibrosis area estimation. Liver Int. 2003;23:28-34. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 37] [Cited by in RCA: 30] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 30. | Dioguardi N, Grizzi F, Bossi P, Roncalli M. Fractal and spectral dimension analysis of liver fibrosis in needle biopsy specimens. Anal Quant Cytol Histol. 1999;21:262-266. [PubMed] |
| 31. | Grizzi F, Dioguardi N. A fractal scoring system for quantifying active collagen synthesis during chronic liver disease. Int J Chaos Theor Appl. 1999;4:39-44. |
| 32. | Dioguardi N, Franceschini B, Aletti G, Russo C, Grizzi F. Fractal dimension rectified meter for quantification of liver fibrosis and other irregular microscopic objects. Anal Quant Cytol Histol. 2003;25:312-320. [PubMed] |
| 33. | Dioguardi N, Grizzi F, Franceschini B, Bossi P, Russo C. Liver fibrosis and tissue architectural change measurement using fractal-rectified metrics and Hurst's exponent. World J Gastroenterol. 2006;12:2187-2194. [PubMed] |
| 34. | Bedossa P, Dargère D, Paradis V. Sampling variability of liver fibrosis in chronic hepatitis C. Hepatology. 2003;38:1449-1457. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1193] [Cited by in RCA: 1398] [Article Influence: 63.5] [Reference Citation Analysis (0)] |
| 35. | Siddique I, El-Naga HA, Madda JP, Memon A, Hasan F. Sampling variability on percutaneous liver biopsy in patients with chronic hepatitis C virus infection. Scand J Gastroenterol. 2003;38:427-432. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 123] [Cited by in RCA: 122] [Article Influence: 5.5] [Reference Citation Analysis (0)] |
| 36. | Olsson R, Hägerstrand I, Broomé U, Danielsson A, Järnerot G, Lööf L, Prytz H, Rydén BO, Wallerstedt S. Sampling variability of percutaneous liver biopsy in primary sclerosing cholangitis. J Clin Pathol. 1995;48:933-935. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 98] [Cited by in RCA: 90] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 37. | Imamura H, Kawasaki S, Bandai Y, Sanjo K, Idezuki Y. Comparison between wedge and needle biopsies for evaluating the degree of cirrhosis. J Hepatol. 1993;17:215-219. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 14] [Cited by in RCA: 8] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 38. | Gluud C. Sampling variability in percutaneous liver biopsy. Lancet. 1986;1:975. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2] [Cited by in RCA: 2] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 39. | Maharaj B, Maharaj RJ, Leary WP, Cooppan RM, Naran AD, Pirie D, Pudifin DJ. Sampling variability and its influence on the diagnostic yield of percutaneous needle biopsy of the liver. Lancet. 1986;1:523-525. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 461] [Cited by in RCA: 462] [Article Influence: 11.8] [Reference Citation Analysis (0)] |
| 40. | Layden TJ. Percutaneous needle biopsy specimens. Sampling variability in patients with chronic hepatitis and cirrhosis. Arch Intern Med. 1979;139:856. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 4] [Cited by in RCA: 3] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 41. | Abdi W, Millan JC, Mezey E. Sampling variability on percutaneous liver biopsy. Arch Intern Med. 1979;139:667-669. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 163] [Cited by in RCA: 150] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 42. | Dioguardi N, Franceschini B, Russo C, Grizzi F. Computer-aided morphometry of liver inflammation in needle biopsies. World J Gastroenterol. 2005;11:6995-7000. [PubMed] |
| 43. | Junqueira LC, Bignolas G, Brentani RR. Picrosirius staining plus polarization microscopy, a specific method for collagen detection in tissue sections. Histochem J. 1979;11:447-455. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1745] [Cited by in RCA: 1851] [Article Influence: 40.2] [Reference Citation Analysis (0)] |
| 44. | Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal Physiology. New York: Oxford University Press 1994; . [DOI] [Full Text] |
| 45. | Hastings HM, Sugihara G. Fractals. A User's Guide for the Natural Sciences. Oxford: Oxford Science Publications 1993; . |
| 46. | Dioguardi N, Grizzi F. Fractal dimension exponent for quantitative evaluation of liver collagen in bioptic specimens. Basel, Boston, Berlin: Birkhauser Press 2001; 113-120. |
| 47. | Hurst HE. Long-term storage capacity of reservoirs. Trans Am Soc Civ Eng. 1951;116:770-808. |
| 48. | Hurst HE, Black RP, Simaiki YM. Long-term storage: an experimental study. London: Constable 1965; . |
| 49. | Bassingthwaighte JB, Raymond GM. Evaluation of the dispersional analysis method for fractal time series. Ann Biomed Eng. 1995;23:491-505. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 108] [Cited by in RCA: 68] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 50. | Herrine SK, Friedman LS. Divining the role of liver biopsy in hepatitis C. J Hepatol. 2005;43:374-376. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 7] [Cited by in RCA: 7] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 51. | Afdhal NH. Biopsy or biomarkers: is there a gold standard for diagnosis of liver fibrosis. Clin Chem. 2004;50:1299-1300. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 42] [Cited by in RCA: 39] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 52. | Afdhal NH. Diagnosing fibrosis in hepatitis C: is the pendulum swinging from biopsy to blood tests. Hepatology. 2003;37:972-974. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 92] [Cited by in RCA: 93] [Article Influence: 4.2] [Reference Citation Analysis (0)] |
| 53. | Tao J, Peng HQ, Cai WM, Dong FQ, Weng HL, Liu RH. Influence factors of serum fibrosis markers in liver fibrosis. World J Gastroenterol. 2003;9:2497-2500. [PubMed] |
| 54. | Zheng M, Cai WM, Weng HL, Liu RH. ROC curves in evaluation of serum fibrosis indices for hepatic fibrosis. World J Gastroenterol. 2002;8:1073-1076. [PubMed] |
| 55. | Rosenthal-Allieri MA, Peritore ML, Tran A, Halfon P, Benzaken S, Bernard A. Analytical variability of the Fibrotest proteins. Clin Biochem. 2005;38:473-478. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 31] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 56. | Ghany MG, Doo E. Assessment of liver fibrosis: palpate, poke or pulse. Hepatology. 2005;42:759-761. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 14] [Cited by in RCA: 18] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 57. | Dufour DR. Assessment of liver fibrosis: Can serum become the sample of choice. Clin Chem. 2005;51:1763-1764. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 7] [Cited by in RCA: 7] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 58. | Wanless IR. Liver biopsy in the diagnosis of hepatocellular carcinoma. Clin Liver Dis. 2005;9:281-5, vii. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 14] [Cited by in RCA: 12] [Article Influence: 0.6] [Reference Citation Analysis (0)] |