Published online Dec 26, 2017. doi: 10.5662/wjm.v7.i4.112
Peer-review started: October 29, 2017
First decision: November 20, 2017
Revised: November 23, 2017
Accepted: December 3, 2017
Article in press: December 3, 2017
Published online: December 26, 2017
Processing time: 58 Days and 10.4 Hours
A statistically significant research finding should not be defined as a P-value of 0.05 or less, because this definition does not take into account study power. Statistical significance was originally defined by Fisher RA as a P-value of 0.05 or less. According to Fisher, any finding that is likely to occur by random variation no more than 1 in 20 times is considered significant. Neyman J and Pearson ES subsequently argued that Fisher’s definition was incomplete. They proposed that statistical significance could only be determined by analyzing the chance of incorrectly considering a study finding was significant (a Type I error) or incorrectly considering a study finding was insignificant (a Type II error). Their definition of statistical significance is also incomplete because the error rates are considered separately, not together. A better definition of statistical significance is the positive predictive value of a P-value, which is equal to the power divided by the sum of power and the P-value. This definition is more complete and relevant than Fisher’s or Neyman-Peason’s definitions, because it takes into account both concepts of statistical significance. Using this definition, a statistically significant finding requires a P-value of 0.05 or less when the power is at least 95%, and a P-value of 0.032 or less when the power is 60%. To achieve statistical significance, P-values must be adjusted downward as the study power decreases.
Core tip: Statistical significance is currently defined as a P-value of 0.05 or less, however, this definition is inadequate because of the effect of study power. A better definition of statistical significance is based upon the P-value’s positive predictive value. To achieve statistical significance using this definition, the power divided by the sum of power plus the P-value must be 95% or greater.
- Citation: Heston TF, King JM. Predictive power of statistical significance. World J Methodol 2017; 7(4): 112-116
- URL: https://www.wjgnet.com/2222-0682/full/v7/i4/112.htm
- DOI: https://dx.doi.org/10.5662/wjm.v7.i4.112
Scientific research has long utilized and accepted that a research finding is statistically significant if the likelihood of observing the statistical significance equates to P < 0.05. In other words, the result could be attributed to luck less than 1 in 20 times. If we are testing for example, effects of drug A on effect B, we could stratify groups into those receiving therapy vs those taking placebo vs no pharmacological intervention. If the data resulted in a P-value less than 0.05, under the generally accepted definition, this would suggest that our results are statistically significant. However, it could be equally argued that had it resulted in a P-value of 0.06, or just above the generally accepted cutoff of 0.05, it is still statistically significant, but to a slightly lesser degree - an index of statistical significance rather than a dichotomous yes or no. In that case, further testing may be indicated to validate the results but perhaps not enough evidence to outright conclude that the null hypothesis, drug A has no effect, is accurate in this sense.
The originator of this idea of a statistical threshold was the famous statistician R. A. Fisher who in his book Statistical Methods for Research Workers, first proposed hypothesis testing using an analysis of variance P value[1]. In his words, the importance of statistical significance in biological investigation is to “prevent us being deceived by accidental occurrences” which are “not the causes we wish to study, or are trying to detect, but a combination of the many other circumstances which we can not control”[2]. His argument was that P ≤ 0.05 was a convenient level of standardization to hold researchers to, but that it is not a definitive rule as an arbitrary number. It is ultimately the responsibility of the investigator to evaluate the significance of their obtained data and P-value. For example, in some cases, a P-value of 0.05 may indicate further investigation is warranted while in others that may suffice.
There were however, opposing viewpoints to this idea, namely that of Neyman J and Pearson ES who argued for more for a “hypothesis testing” rather than “significance testing” as Fisher had postulated[3]. Neyman and Pearson[4] raised the question that Fisher failed to, namely that with data interpretation there may be not only a type I error, but a type II error (accepting the null hypothesis when it should in fact be rejected). They famously stated “Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behavior with regard to them, in following which we insure that, in the long run of experience, we shall not be too often wrong”[4]. Part of the Neyman-Pearson approach includes researchers assigning prior to an experiment, the alternative hypothesis which should be specific such that drug X has Y effect by 30%[5]. This hypothesis is later accepted or rejected based on the P-value whose threshold was arbitrarily set at 0.05.
These two viewpoints between Neyman-Pearson and the more subjective view of Fisher were heavily debated and are ultimately recognized as either the Neyman-Pearson approach or the Fisher approach. In today’s academic setting, the determination of statistical variance with a P-value has truly become dichotomous, either rejection or acceptance based on P < 0.05, rather than more of an index of suspicion as Fisher had originally proposed. However, an approach of confidence based on the P-value could be beneficial rather than a definitive decision based on an arbitrary cutoff.
The meaning and use of statistical significance as originally defined by Fisher RA, Jerzy Neyman and Egon Pearson has undergone little change in the almost 100 years since originally proposed. Statistical significance as original proposed by Fisher’s P-value was the determination of whether or not a finding was unusual and worthy of further investigation. The Neyman-Pearson proposal was similar but slightly different. They proposed the concepts of alpha and beta with the alpha level representing the chance of erroneously thinking there is a significant finding (a Type I error) and the beta level representing the chance of erroneously thinking there is no significant finding (a Type II error) in the data observed[6].
Statistical significance as currently used represents the chance that the null hypothesis is not true as defined by the P-value. The classic definition of a statistically significant result is when the P-value is less than or equal to 0.05, meaning that there is at most a one in twenty chance that the test statistic found is due to normal variation of the null hypothesis[2]. So when researchers state that their findings are “statistically significant” what they mean is that if in reality there was no difference between the groups studied, their findings would randomly occur at most only once out of twenty trials.
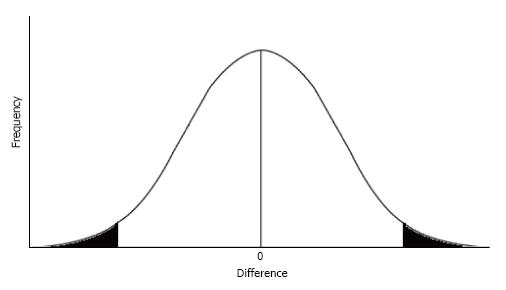
For example, consider an experiment in which there is no true difference between a placebo and an experimental drug. Because of normal random variation, a frequency distribution graph representing the difference between subjects taking a placebo compared with those taking the experimental drug typically forms a bell shaped curve[7]. When there is no true difference between the placebo and the experimental drug, small differences will occur frequently and cluster around zero, the center of the peak of the curve. Relatively large differences will also occur, albeit infrequently, and these results are represented by the upper and lower tails of the graph. Assuming the entire area under the bell shaped curve equals 1, as represented in Figure 1, the findings are assumed to be statistically significant when the difference found falls in either the lower or upper 2.5% of the frequency distribution[8].
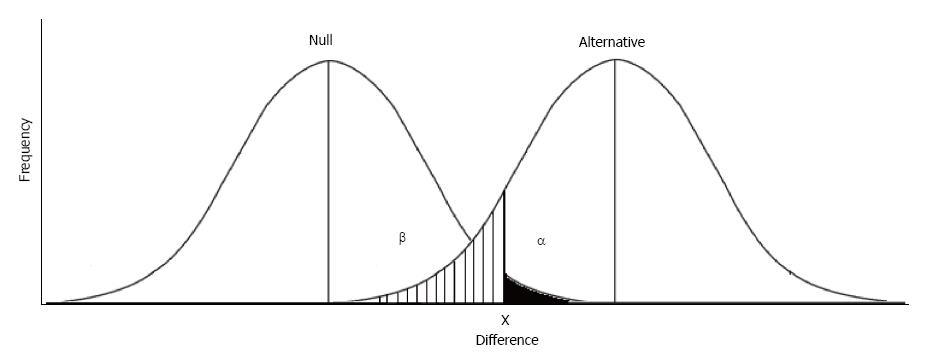
Note that the classical definition of statistical significance according to Fisher relies only upon a single frequency distribution curve, representing the null hypothesis that no true difference exists between the two groups observed[9]. Fisher’s approach makes the primary assumption that only one group exists, as represented by a single frequency distribution curve, and P-values (the likelihood of a large difference being observed) define statistical significance. The Neyman-Pearson approach is slightly different, in that the primary assumption is that two groups exist, and two frequency distributions are necessary[10]. In this approach, the tail of the frequency distribution representing the null hypothesis (no difference) is represented by alpha (α). Similar to the P-value, alpha represents the chance of rejecting the null hypothesis when in fact it is true, a Type I error[11]. The tail of the frequency distribution representing the alternative hypothesis (a true difference exists) is represented by beta (β). Beta represents the chance of rejecting the alternative hypothesis when in fact it is true, a Type II error. If we are doing a one-tailed comparison, e.g., when we assume the experimental drug will improve but not hurt patients, alpha and beta can be visualized in Figure 2. The area in black represents a Type I error and the lined area represents a Type II error.
It is time that the statistical significance be defined not just as the chance that the null hypothesis is not true (a low P-value), or the likelihood of error when accepting (α) or rejecting (β) the null hypothesis. While these statistics help us evaluate research data, they do not give us the odds of being right or wrong, which requires that we analyze both the P-value with β together[12].
While it is helpful to visualize the concepts of alpha and beta on frequency distribution graphs, it is additionally illuminating to compare these concepts with sensitivity, specificity, and predictive values obtained from 2 × 2 contingency tables. In Table 1, the rows represent our statistical test results, and the columns represent what is actually true. Row 1 represents the situation when our data analysis results in a P-value of ≤ 0.05, and row 2 represents the situation when our analysis results in a P-value of > 0.05. The columns represent reality. Column 1 represents the situation when the alternative hypothesis is in reality true, and column 2 represents the situation when the null hypothesis in reality is true.
| Reality | |||
| Study findings | Alternative hypothesis true | Null hypothesis true | |
| Significant P-value ≤ 0.05 | True positive | False positive | |
| Insignificant P-value > 0.05 | False negative | True negative | |
In Table 1, row 1 column 1 are the true positives because the P-value is ≤ 0.05 and the alternative hypothesis is true. Row 1 column 2 are false positives, because even though the P-value is ≤ 0.05, the reality is that there is no significant difference and the null hypothesis is true. Similarly, row 2 column 1 are the false negatives because the P-value is insignificant (P > 0.05) but in reality the alternative hypothesis is true. Row 2 column 2 are the true negatives because the P-value is insignificant and the null hypothesis is true.
Table 2 shows our findings in terms of alpha and beta. In this case, alpha represents the exact P-value, not just whether or not the P-value is ≤ 0.05. Beta is not only the chance of a Type II error (a false negative), it is used to determine the study’s power which is simply equal to 1 - beta. Table 3 shows the same information in another way, showing the situations in which our test of statistical significance, the P-value, is in fact correct or is in error.
| Reality | |||
| Study findings | Alternative hypothesis true | Null hypothesis true | |
| Significant P-value ≤ 0.05 | 1 - beta (power) | Alpha (exact P-value) | |
| Insignificant P-value > 0.05 | Beta | 1 - alpha | |
| Reality | |||
| Study findings | Alternative hypothesis true | Null hypothesis true | |
| Significant P-value ≤ 0.05 | Correct | Type I error | |
| Insignificant P-value > 0.05 | Type II error | Correct | |
When we know beta and alpha, or alternatively the P-value and power of the study, we can fill out the contingency table and answer our real question of how likely is it that our findings represent the truth. Statistical power, equal to 1 - beta, is typically set in advance to help determine sample size. A typical level recommended for power is 0.80[13]. Table 4 is an example 2 × 2 contingency table in the which the study has a power of 0.80 and the analysis finds a statistically significant result of P = 0.05. In this situation, the sensitivity of the test statistic equals the power, or 0.8/(0.8 + 0.2). The specificity of the test statistic is 1 minus alpha, or 0.95/(0.05 + 0.95). Our positive predictive value is power divided by the sum of power and the exact P-value, or 0.80/(0.80 + 0.05). The negative predictive value is the specificity divided by the sum of the specificity and beta, or 0.95/(0.95 + 0.20).
| Reality | |||
| Study findings | Alternative hypothesis true | Null hypothesis true | |
| Significant P-value ≤ 0.05 | 0.8 | 0.05 | |
| Insignificant P-value > 0.05 | 0.2 | 0.95 | |
To be 95% confident that the P-value represents a statistically significant result, the positive predictive value must be 95% or greater. In the standard situation where the study power is 0.80, a P-value of 0.42 or less is required to achieve this level of confidence. As shown in Table 5, a power of 0.95 is required for a P-value of 0.05 to indicate a 95% or greater confidence that the study’s findings are statistically significant. If the power falls to 90%, a P-value of 0.047 or less is required to be 95% confident that the alternative hypothesis is true (i.e., a 95% positive predictive value). If the power is only 60%, then a P-value of 0.032 or less is required to be 95% confident that the alternative hypothesis is true. To determine how likely a study’s findings represent the truth, determine the positive predictive value (PPV) of the test statistic:
| Study power | P-value |
| 0.95 | 0.05 |
| 0.9 | 0.047 |
| 0.85 | 0.045 |
| 0.8 | 0.042 |
| 0.75 | 0.039 |
| 0.7 | 0.037 |
| 0.65 | 0.034 |
| 0.6 | 0.032 |
PPV = power/(power + P-value)
To determine the required P-value to achieve a 95% PPV:
P-value = (power - 0.95 * power)/0.95
In the situation where the P-value is greater than the cutoff values determined by the preceding method, it is helpful to determine just how confident we can be that the null hypothesis is correct. This simply entails calculating the negative predictive value of the test statistic:
NPV = (1 - alpha)/(1 + beta - alpha)
Finally, using this method we can determine the overall accuracy of a research study. Prior to collecting and analyzing the research data, pre-set values are determined for power and a cutoff P-value for statistical significance. If we want to be 95% confident that a research study will correctly identify reality, a pre-set power of 95% along with a pre-set cutoff P-value of 0.05 is required. At a pre-set power of 90%, a pre-set cutoff P-value of 0.01 is required. When the pre-set power is 80% or less, the maximum confidence in the accuracy of the study findings is at most 90% even when a pre-set P-value cutoff is extremely low. To determine the maximum level of confidence a study can have at a specific level of power and cutoff P-value (alpha), calculate the accuracy:
Accuracy = (1 + power - alpha)/2
Statistical significance has for too long been broadly defined as a P-value of 0.05 or less[14]. Using the P-value alone can be misleading because its calculation does not take into account the effect of study power upon the likelihood that the P-value represents normal variation or a true difference in study populations[15]. If we want to be at least 95% confident that a research study has identified a true difference in study populations, the power must be at least 95%. If the power is lower, the required P-value to indicate a statistically significant result needs to be adjusted downward according to the formula P-value = (power - 0.95*power)/0.95. Furthermore, by using the positive predictive value of the P-value, not just the P-value alone, researchers and readers are able to better understand the level of confidence they can have in the findings and better assess clinical relevance[16]. Only when the power of a study is at least 95% does a P-value of 0.05 or less indicate a statistically significant result.
Manuscript source: Invited manuscript
Specialty type: Medical laboratory technology
Country of origin: United States
Peer-review report classification
Grade A (Excellent): A
Grade B (Very good): 0
Grade C (Good): 0
Grade D (Fair): 0
Grade E (Poor): 0
P- Reviewer: Dominguez A S- Editor: Ji FF L- Editor: A E- Editor: Lu YJ
| 1. | Fisher RA. Intraclass correlations and the analysis of variance. Statistical methods for research workers. Edinburgh: Oliver and Boyd 1934; 198-235. |
| 2. | Fisher RA. The statistical method in psychical research. Proceedings of the Society for Psychical Research. University Library Special Collections. 1929;39:189-192. |
| 3. | Lehmann EL. The Fisher, Neyman-Pearson theories of testing hypotheses: one theory or two? J Am Stat Assoc. 1993;88:1242-1249. [RCA] [DOI] [Full Text] [Cited by in Crossref: 191] [Cited by in RCA: 96] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 4. | Neyman J, Pearson ES. On the problem of the most efficient tests of statistical hypotheses. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 1933; 289-337. [RCA] [DOI] [Full Text] [Cited by in Crossref: 1627] [Cited by in RCA: 1645] [Article Influence: 58.8] [Reference Citation Analysis (0)] |
| 5. | Sterne JA, Davey Smith G. Sifting the evidence-what’s wrong with significance tests? BMJ. 2001;322:226-231. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 117] [Cited by in RCA: 119] [Article Influence: 5.0] [Reference Citation Analysis (0)] |
| 6. | Hubbard R, Bayarri MJ. Confusion over measures of evidence (p ‘s) versus errors (α’s) in classical statistical testing. The American Statistician. 2003;57:171-178. [RCA] [DOI] [Full Text] [Cited by in Crossref: 179] [Cited by in RCA: 97] [Article Influence: 4.4] [Reference Citation Analysis (0)] |
| 7. | Hazra A, Gogtay N. Biostatistics Series Module 1: Basics of Biostatistics. Indian J Dermatol. 2016;61:10-20. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 7] [Cited by in RCA: 8] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 9. | Hansen JP. Can’t miss: conquer any number task by making important statistics simple. Part 6. Tests of statistical significance (z test statistic, rejecting the null hypothesis, p value), t test, z test for proportions, statistical significance versus meaningful difference. J Healthc Qual. 2004;26:43-53. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 6] [Cited by in RCA: 7] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 10. | Bradley MT, Brand A. Significance Testing Needs a Taxonomy: Or How the Fisher, Neyman-Pearson Controversy Resulted in the Inferential Tail Wagging the Measurement Dog. Psychol Rep. 2016;119:487-504. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 11] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 11. | Imberger G, Gluud C, Boylan J, Wetterslev J. Systematic Reviews of Anesthesiologic Interventions Reported as Statistically Significant: Problems with Power, Precision, and Type 1 Error Protection. Anesth Analg. 2015;121:1611-1622. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 77] [Cited by in RCA: 87] [Article Influence: 9.7] [Reference Citation Analysis (0)] |
| 12. | Heston T. A new definition of statistical significance. J Nucl Med. 2013;54:1262. [DOI] [Full Text] |
| 13. | Bland JM. The tyranny of power: is there a better way to calculate sample size? BMJ. 2009;339:b3985. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 70] [Cited by in RCA: 77] [Article Influence: 4.8] [Reference Citation Analysis (0)] |
| 14. | Johnson DH. The insignificance of statistical significance testing. J Wildlife Manage. 1999;63:763. [RCA] [DOI] [Full Text] [Cited by in Crossref: 656] [Cited by in RCA: 659] [Article Influence: 25.3] [Reference Citation Analysis (0)] |
| 15. | Moyé LA. P-value interpretation and alpha allocation in clinical trials. Ann Epidemiol. 1998;8:351-357. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 43] [Cited by in RCA: 35] [Article Influence: 1.3] [Reference Citation Analysis (0)] |
| 16. | Heston T, Wahl R. How often are statistically significant results clinically relevant? not often. J Nucl Med. 2009;50:1370. [DOI] [Full Text] |