Revised: November 5, 2012
Accepted: December 6, 2012
Published online: March 26, 2013
AIM: To describe confidence interval calculation for antidotal potency ratios using bootstrap method.
METHODS: We can easily adapt the nonparametric bootstrap method which was invented by Efron to construct confidence intervals in such situations like this. The bootstrap method is a resampling method in which the bootstrap samples are obtained by resampling from the original sample.
RESULTS: The described confidence interval calculation using bootstrap method does not require the sampling distribution antidotal potency ratio. This can serve as a substantial help for toxicologists, who are directed to employ the Dixon up-and-down method with the application of lower number of animals to determine lethal dose 50 values for characterizing the investigated toxic molecules and eventually for characterizing the antidotal protections by the test antidotal systems.
CONCLUSION: The described method can serve as a useful tool in various other applications. Simplicity of the method makes it easier to do the calculation using most of the programming software packages.
- Citation: Manage A, Petrikovics I. Confidence limit calculation for antidotal potency ratio derived from lethal dose 50. World J Methodol 2013; 3(1): 7-10
- URL: https://www.wjgnet.com/2222-0682/full/v3/i1/7.htm
- DOI: https://dx.doi.org/10.5662/wjm.v3.i1.7
To characterize toxic effects of poisons and overdosed drugs, acute toxicity testing methods were developed in the beginning of the 19th century. Trevan[1] first wrote up the concept of lethal dose 50 (LD50) (medium lethal dose) in 1927. He also indicated that LD50 is not a biological constant, its precision depends on many factors (e.g., number of animals used, sex, species, strain, age, diet, general health condition, route of administration, stress, formulation, intra and inter laboratory variations, etc.). To express acute toxicity, LD50 is a good tool, and many government agencies still rely on these data. Many methods have been developed to characterize the toxic effects (acute toxicity) of chemicals, and expressed as LD50 values and its 95% confidence limit and the slope of the probit line, e.g., Litchfield and Wilcoxon[2], Bliss[3], Holland et al[4]. Up until the 90s, the Litchfield and Wilcoxon[2] method was one of the most frequently used tool for toxicologists to characterize acute toxicity, and the in vivo antidotal efficacy of various antidotal systems.
An example, Pei et al [5], analyzed data for LD50 values of paraoxon that is an organophosphorus (OP) type nerve agent, in the presence of various antidotal systems by the method of Litchfield and Wilcoxon, as adapted to a computer program PHARM/PCS version 4.2. by Bergol’ts et al[6]. The antidotal potency ratios (APRs) derived from the dose-response curves of paraoxon were used to express the in vivo efficacy of various OP antidotal systems to antagonize the lethal effects of paraoxon (APR = LD50 of paraoxon antagonized/LD50 of paraoxon unantagonized). Tests for the parallelism of the dose-effect curves were done, and all statistical procedures were performed at the 95% confidence level. The authors used six groups of animals, 8 animals per groups (48 animals) for each LD50 value.
Since the Litchfield-Wilcoxon method requires a large number (40-50) of animals, efforts were done to introduce other LD50 determinations with a lesser number of animals. The up-and-down methods by Dixon[7], Bruce[8] can provide adequate estimation of LD50 and approximation of the 95% confidence interval by using as few as 6-9 animals. When this method was compared with the traditional Litchfield-Wilcoxon method, excellent agreement was obtained for all the 10 molecules tested.
Another example: Petrikovics et al [9], determined LD50 values for paraoxon by the method of Dixon[6], and 95% confidence limit was estimated by the method of Bruce[10]. For each experiment, 6-10 animals were used. The LD50 values were calculated from the equation of Log (LD50) = log (dose final) + k log (d) where dose final is the final dose administered, k is the tabular value from the table, and d is the interval between doses. APRs were expressed as a simple number (without confidence limit). APR = mean LD50 of paraoxon antagonized/mean LD50 of paraoxon unantagonized.
Another example: Petrikovics et al[11], determined LD50 for cyanide by the up-and-down method of Dixon[7]. This method requires settings for the starting doses and the stage distances (dose difference between doses) for each test system. The software (based on “Implementation of Dixon and Massey UPD”, Introduction to statistical Analysis, 1983, pp.434-438) provides information for the next dose for each stage, based on the mortality results for the given stage. The log dose difference of 0.1 was set up based on the earlier studies with cyanide (Petrikovics et al[12], where the LD50 values were determined by the classic Litchfield-Wilcoxon[2] method. For each LD50 values 10-18 were used. LD50 values were expressed as average ± 95% confidence limit by the software. APRs were expressed as a ratio of average LD50 of cyanide with antidotes and average LD50 of cyanide without antidotes. Again, confidence limits for APR were not expressed.
In a situation like this where the distribution of the ratio is unknown, it is difficult to calculate the confidence intervals using classical methods. However, we can easily adapt the nonparametric bootstrap method which was invented by Efron[13] to construct confidence intervals in such situations like this. The bootstrap method is a resampling method in which the bootstrap samples are obtained by resampling from the original sample. A comprehensive coverage of the bootstrap method can be found in Efron and Tibshirani[14]. Chernick[15], Shao and Tu[16], Davison and Hinkley[17], Manly[18] and Hayden[19] are also useful references.
There are several ways of calculating bootstrap confidence intervals. Briefly, one way of calculating the bootstrap confidence interval for APR given below:
To assume that the data set is coming from two samples which we call sample 1 and sample 2 to calculate the APR.
(1) Obtain a bootstrap sample X* = (X1*, X2*,......, Xn1*) from the original sample 1 X = (X1, X2,......, Xn1).
(2) Calculate logLD50 dose estimate using
[page 389 Dixon (1969)];
(3) Obtain a bootstrap sample Y* = (Y1*, Y2*,......, Yn1*) from the original sample 2 Y = (Y1, Y2,......, Yn1);
(4) Calculate logLD50 dose estimate using,
(5) Calculate the ratio,
(as the values are in log base 10);
(6) Repeat step 1 through step 5, a large number of times (B = 1000) to get a list of values;
(7) Find the quantiles APR(α/2) and APR(1-α/2) for the list of B ratio values. (APRα/2, APR1-α/2) is the 100 (1 - α)% confidence interval for the ratio. This confidence interval is usually called percentile bootstrap confidence interval.
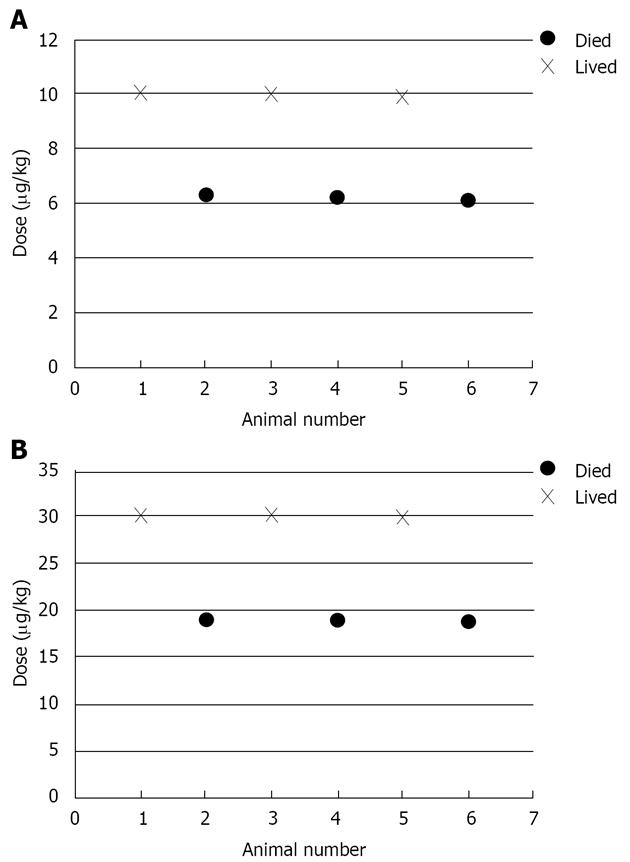
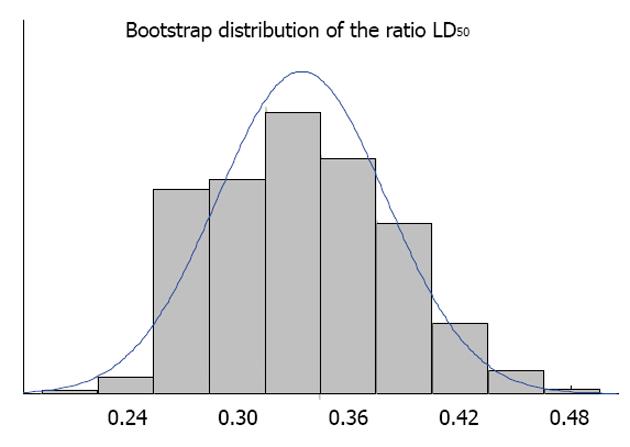
We illustrate the method for LD50 ratio for the following two experiments (Figure 1). Figure 2 shows the histogram of the bootstrap distribution of the APR. Quantiles of this distribution are used to derive the relevant confidence limits. In our illustration here we use the 95% confidence limit. LD50 dose estimate for the first experiment is 7.834 and the LD50 dose estimate for the second experiment is 23.812. This gives the APR to be 0.32897. Therefore, the lower confidence limit, which is the 2.5th percentile of the bootstrap distribution is 0.25821 and the upper confidence limit which is the 97.5th percentile of the bootstrap distribution is 0.41714.
We used a simple method to construct the confidence interval for calculating APR derived from two LD50. The described nonparametric bootstrap method to determine confidence intervals can easily be constructed even in situations where the distribution of the ratio is unknown. This presentation describes a calculation of the bootstrap confidence interval for APR. This can serve as a substantial improvement for toxicologists, who are directed to employ the Dixon up-and-down method with the application of lower number of animals to determine LD50 values for characterizing the investigated toxic molecules and eventually for characterizing the antidotal protections by the test antidotal systems. The described method can serve as a useful tool in various other applications. Simplicity of the method makes it easier to do the calculation using most of the programming software packages.
To characterize toxic effects of poisons and overdosed drugs, acute toxicity testing methods were developed in the beginning of the 19th century. To express acute toxicity, lethal dose 50 (LD50) is a good tool, and many government agencies still rely on these data. Many methods have been developed to characterize the toxic effects (acute toxicity) of chemicals, and expressed as LD50 values and its 95% confidence limit and the slope of the probit line. To characterize antidotal efficacy of a given antidotal system, antidotal potency ratios (APRs) are calculated, that is the ratio of the LD50 of the toxic chemical with the test antidotal system and the LD50 of the toxic chemicals without any antidote(s) (control). The higher is the APR, the better is the antidotal system.
When applying the classic Litchfield-Wilcoxon method for LD50 determination, a large number of animals (6-8 groups of animals, 6-8 animal/group = 36-64) are needed. To reduce the number of animals, new methods were developed, and the Dixon up-and-down method has become popular with its lower number of animal needed (8-18 animals/LD50). However, when the Litchfield-Wilcoxon method was adapted to a computer program PHARM/PCS version 4.2. by Tallarida and Murray, the APR was automatically expressed with 95% confidence limits by the software. There is a need for the 95% confidence limit determination with the Dixon up-and-down method when expressing APR values. Although Bruce provided adequate estimation for it, this article introduces a more practical tool for filling this gap.
Previous methods to characterize acute toxicity and/or determining antidotal efficacy for antidotal systems needed to be transformed in order to (1) reduce the number of animals used for LD50 determination (2) calculate 95% confidence limits for APR with lower number of animals used. This article can serve as a substantial help for toxicologists, who are directed to employ the Dixon up-and-down method with the application of lower number of animals to determine LD50 values for characterizing the investigated toxic molecules and eventually for characterizing the antidotal protections by the test antidotal systems.
The described method can serve as a useful tool in various other applications. Simplicity of the method makes it easier to do the calculation using most of the programming software packages. Authors used a simple MATLAB code to illustrate the confidence interval for the given example.
LD50 is the dose that kills 50% of the tested animal population. APR = LD50 of the toxic chemicals in the presence of the test antidotal system(s)/LD50 of the toxic chemical without any antidote(s) (control). APR is use to express in vivo efficacy for antidotal systems. Bootstrap method is a standard technique in which we take simple random samples with replacement from the original sample. With this, overlapping samples is permissible in this technique. Strength of the paper is the application of the bootstrap method to calculate a confidence interval for the LD50 ratio. Validation of the method proven practically and theoretically in the literature.
This is a good practical method to express 95% confidence limits for APR derived from the Dixon up-and-down method.
P- Reviewers Hutz RJ, Dhawan DK, Wan TTH S- Editor Zhai HH L- Editor A E- Editor Xiong L
| 1. | Trevan JW. The error of determination of toxicity. Proc R Soc Lond. 1927;101:483-514. [RCA] [DOI] [Full Text] [Cited by in Crossref: 244] [Cited by in RCA: 240] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 2. | Litchfield JT, Wilcoxon F. A simplified method of evaluating dose-effect experiments. J Pharmacol Exp Ther. 1949;96:99-113. [PubMed] |
| 4. | Holland KD, McKeon AC, Canney DJ, Covey DF, Ferrendelli JA. Relative anticonvulsant effects of GABAmimetic and GABA modulatory agents. Epilepsia. 1992;33:981-986. [PubMed] |
| 5. | Pei L, Petrikovics I, Way JL. Antagonism of the lethal effects of paraoxon by carrier erythrocytes containing phosphotriesterase. Fundam Appl Toxicol. 1995;28:209-214. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 28] [Cited by in RCA: 23] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 6. | Bergol’ts VV, Volodin IuIu. [A package of applied programs for pharmacological and biochemical calculations]. Farmakol Toksikol. 1987;50:70-73. [PubMed] |
| 7. | Dixon WJ. The up-and-down method for small animal samples. Am Stat Assoc J. 1965;12:967-978. [DOI] [Full Text] |
| 8. | Bruce RD. An Up-and-Down procedure for acute toxicity testing. Fundam Appl Toxico. 1985;5:15-157. [RCA] [DOI] [Full Text] [Cited by in Crossref: 234] [Cited by in RCA: 205] [Article Influence: 5.1] [Reference Citation Analysis (0)] |
| 9. | Petrikovics I, Hong K, Omburo G, Hu QZ, Pei L, McGuinn WD, Sylvester D, Tamulinas C, Papahadjopoulos D, Jaszberenyi JC. Antagonism of paraoxon intoxication by recombinant phosphotriesterase encapsulated within sterically stabilized liposomes. Toxicol Appl Pharmacol. 1999;156:56-63. [PubMed] |
| 10. | Bruce RD. A confirmatory study of the up-and-down method for acute oral toxicity testing. Fundam Appl Toxicol. 1987;8:97-100. [PubMed] |
| 11. | Petrikovics I, Baskin SI, Beigel KM, Schapiro BJ, Rockwood GA, Manage AB, Budai M, Szilasi M. Nano-intercalated rhodanese in cyanide antagonism. Nanotoxicology. 2010;4:247-254. [PubMed] |
| 12. | Petrikovics I, Pei L, McGuinn WD, Cannon EP, Way JL. Cyanide antagonism with organic thiosulfonates and carrier red blood cells containing rhodanese. Fund Appl Toxicol. 1995;24:1-8. [RCA] [DOI] [Full Text] [Cited by in Crossref: 46] [Cited by in RCA: 45] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 13. | Efron B. Bootstrap methods: another look at the jackknife. Ann Statist. 1979;7:1-26. [RCA] [DOI] [Full Text] [Cited by in Crossref: 10059] [Cited by in RCA: 10231] [Article Influence: 222.4] [Reference Citation Analysis (0)] |
| 14. | Efron B, Tibshirani RJ. An Introduction to the Bootstrap. New York: Chapman and Hall 1993; . |
| 15. | Chernick M. Bootstrap Methods: A practitioner’s Guide. New York: Wiley 2007; . |
| 16. | Shao J, Tu D. The Jackknife and Boostrap. New York: Springer 1995; . [DOI] [Full Text] |
| 17. | Davidson A, Hinkley D. Boostrap Method and Their Applications. Cambridge: Cambridge University Press 1997; . |
| 18. | Manly BFJ. Randomization, Bootstrap and Monte Carlo Methods in Biology. Boca Raton, FL: Chapman and Hall/CRC Press 2006; . |
| 19. | Hayden RW. A Review of: “Mathematical Statistics with Resampling and R, by L. M. Chihara and T. C. Hesterberg”. J Biopharm Stat. 2012;22:1287-1288. |