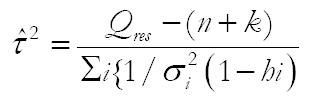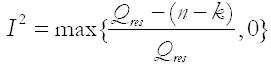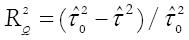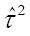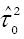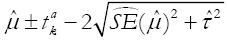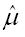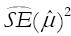Published online Aug 26, 2012. doi: 10.5662/wjm.v2.i4.27
Revised: March 19, 2011
Accepted: July 4, 2012
Published online: August 26, 2012
Aggregate data meta-analysis is currently the most commonly used method for combining the results from different studies on the same outcome of interest. In this paper, we provide a brief introduction to meta-analysis, including a description of aggregate and individual participant data meta-analysis. We then focus the rest of the tutorial on aggregate data meta-analysis. We start by first describing the difference between fixed and random-effects meta-analysis, with particular attention devoted to the latter. This is followed by an example using the random-effects, method of moments approach and includes an intercept-only model as well as a model with one predictor. We then describe alternative random-effects approaches such as maximum likelihood, restricted maximum likelihood and profile likelihood as well as a non-parametric approach. A brief description of selected statistical programs available to conduct random-effects aggregate data meta-analysis, limited to those that allow both an intercept-only as well as at least one predictor in the model, is given. These descriptions include those found in an existing general statistics software package as well as one developed specifically for an aggregate data meta-analysis. Following this, some of the disadvantages of random-effects meta-analysis are described. We then describe recently proposed alternative models for conducting aggregate data meta-analysis, including the varying coefficient model. We conclude the paper with some recommendations and directions for future research. These recommendations include the continued use of the more commonly used random-effects models until newer models are more thoroughly tested as well as the timely integration of new and well-tested models into traditional as well as meta-analytic-specific software packages.
- Citation: Kelley GA, Kelley KS. Statistical models for meta-analysis: A brief tutorial. World J Methodol 2012; 2(4): 27-32
- URL: https://www.wjgnet.com/2222-0682/full/v2/i4/27.htm
- DOI: https://dx.doi.org/10.5662/wjm.v2.i4.27
Meta-analysis is currently the most common approach for quantitatively combining the results of the same outcome from different studies. Indeed, the use of meta-analysis has increased dramatically over the past 30 years. For example, a recent PubMed search by the authors using the keyword “meta-analysis” resulted in 6 hits in the year 1980 vs 6865 hits in the year 2010 (unpublished results). Meta-analysis can be accomplished using either an aggregate data (AD) or individual participant data (IPD) approach. Using an AD approach, summary data for the same outcome from each study, for example, change outcome means and standard deviations for resting systolic blood pressure, are pooled for statistical analysis. In contrast, an IPD meta-analysis includes the pooling of raw data for each participant from each included study. While the IPD approach might be considered the ideal in that it allows for such things as (1) standardizing statistical analyses from each study; (2) obtaining summary results directly, indigenous of study reporting; (3) checking the assumptions of models; (4) assessing participant-level effects; and (5) examining interactions[1], the obtainment of IPD as well as the associated costs for conducting an IPD meta-analysis can be prohibitive[1]. In addition, since the main interest in meta-analysis is often the overall result[2,3], both the IPD and AD approaches should yield similar findings[4,5]. Given these realities, the AD approach continues to be the most commonly used method for pooling the findings of separate studies. Congruent with the use of the AD approach is the need to select a model for combining findings from different studies as well as examining the potential influence of selected covariates on the overall results. Given the former, the purpose of this paper is to provide a brief tutorial of several models currently available for AD meta-analysis, with an emphasis on random-effects models.
The statistical aspects of an AD meta-analysis encompass a two-stage approach. In the first stage, the summary statistics from each study are calculated. In the second stage, these summary statistics from each study are combined to yield an overall result. The focus of this brief tutorial is on the second stage. For a more detailed description of stage one, the reader is referred to the work of Lipsey et al[6].
As previously mentioned, the meta-analyst is often most interested in the overall result(s)[2,3]. Borrowing from Harbord et al[7] and regardless of whether a fixed or random-effects model is used, conducting an AD meta-analysis requires that the analyst be able to derive from study i of n studies an estimate of the outcome of interest (γi) such as a difference in means or log odds ratio, and a standard error of the estimate σi, often which has to be estimated from other data in each study. A fixed-effect meta-analysis assumes that all observed variation is caused by the play of chance, that is, within-study sampling error. Thus, since all studies are assumed to measure the same overall effect, i.e., a single true effect size θ, the intercept-only fixed-effect model can be denoted as γi = θ + εi where εi represents the sampling error for γi.
In contrast, the intercept-only random-effects model allows θi to differ between studies under the assumption of a normal distribution around θ. This can be denoted as γi = θ + εi + μi, where μi represents the between study variance τ2 that must be estimated from the data. Put more simply, a fixed-effect model tests the null hypothesis that there is zero effect in every study while a random-effects model tests the null hypothesis that the mean effect is zero[8]. The fixed-effect model is appropriate for an AD meta-analysis when all included studies are identical and the goal is to estimate a common effect size for the identified population and not generalize to the rest of the population. However, since most researchers are probably interested in generalizing results across a variety of situations and the included studies are unlikely to be functionally equal, the random-effects model is usually the more appropriate model[8,9].
In addition to generating an overall effect size from the pooling of studies, one may also be interested in looking at the effect of potential covariates on the overall effect size, especially, but not exclusively, when significant between-study heterogeneity exists. Since the random vs fixed-effect model is usually the more appropriate model to use, we focus our discussion on the random-effects model in the form of regression, i.e., meta-regression. This is denoted as γi = xiβ + μi + εi, where the single linear covariate (predictor) xiβ replaces the mean θ.
Several different types of random-effects meta-regression models have been recommended for use in an AD meta-analysis, the primary difference being in the calculation of the between-study variance τ2[10]. These models may be better described as mixed-effects models when covariates are included. However, in order to avoid confusion, they will continue to be described as random-effects models.
Regardless of the model chosen, random-effects meta-regression models will initially estimate τ2, the between-study variance, followed by β, the regression coefficients. The regression coefficients are calculated using weighted least squares, 1/(σi2 + τ2), where σi2 represents the standard error of the estimated effect size from study i.
Currently, the most common random-effects meta-regression model used is an extension of the noniterative method of moments approach originally proposed by DerSimonian et al[11]. For this model τ2 is estimated as:[12]
Math 1
where Qres is the residual weighted sum of squares heterogeneity statistic, calculated as:
Math 2
and hi represents the ith diagonal element of the hat matrix X(X’V0-1X)-1 XV01, and V0 = diagonal (σ12,σ22, ... σn2).
Based on the work of Higgins et al[13], the proportion of residual heterogeneity is calculated as:
Math 3
Adjusted R2 (the proportion of between study variance explained by the covariates) is calculated as:
Math 4
where
Math 5
is the estimate of the between-study variance in the model with covariates and
Math 6
is the estimate of the between-study variance without covariates, i.e., intercept-only model.
Summary random-effects estimates do not provide any information regarding how treatment effects from new individual trials are distributed around the summary effect[14]. This may be problematic since the treatment effect is assumed to vary between studies when a random-effects model is used. Recently, prediction intervals have been developed and recommended for determining how treatment effects from new individual trials are distributed about the mean in a random-effects meta- analysis[14]. This is calculated as
Math 7
where
Math 8
is the average weighted estimate across studies,
Math 9
- 2 is the 100 (1 - α/2)% percentile of the t-distribution with k-2 degrees of freedom,
Math 10
is the estimated squared standard error of
Math 11
, and
Math 12
is the estimated between study variance. This is in contrast to obtaining a confidence interval of
Math 13
+ 1.96
Math 14
[14,15]. As previously described in more detail[15], the major point is that the variability between studies, as measured by
Math 15
, needs to be included when making predictions for a new study but not if making inferences about the average effect size. In addition, using the t-distribution vs the normal distribution for prediction intervals is in recognition of the fact that it is estimated rather than being known. Furthermore, it is important to understand that conclusions based on prediction intervals should not be used to determine whether confidence intervals for underlying mean effects are correct or incorrect since prediction intervals are based on a random mean effect while confidence intervals are not.
Data from a previously published meta-analysis of six randomized controlled trials addressing the efficacy of combined aerobic exercise and diet on lipids and lipoproteins in adult men and women at least 18 years of age will serve as the brief example[16]. This dataset reflects the real world of AD meta-analysis with respect to the small number of studies that are usually included and while being mindful that participants are nested within studies, thereby increasing power and precision[17,18]. The focus of the example is on effect size changes in triglycerides, a continuous variable and one of the primary outcomes of the original meta-analysis[16]. At stage one, effect sizes from each study were calculated by subtracting the change score in the intervention group (aerobic exercise and diet) from the change score in the control group. Negative values were indicative of improvements (reductions) in triglycerides. Variances were calculated from the pooled standard deviations of change scores in the intervention and control groups. At stage two, results were pooled using method of moments random-effects meta-regression[11]. While somewhat arbitrary, residual heterogeneity ( ) was classified as small (< 50%), medium (50% to < 75%) and large (≥ 75%)[19]. All data were analyzed using the updated metareg command (version 2.2.6)[7] in version 11.2 of Stata[20].
The intercept-only results are shown in Table 1, Model 1. As can be seen, a statistically significant decrease of approximately 9 mg/dL was observed for triglycerides as a result of a combined aerobic exercise and diet intervention. In addition, non-overlapping confidence intervals were found. However, based on fixed-effect analysis, there was a large amount of residual variation attributable to heterogeneity ( ). This is not uncommon in meta-analysis. The 95% prediction interval for a new trial was -34.08 to 15.35 mg/dL. While a lack of substantial residual heterogeneity should not exclude one from conducting covariate analysis, the presence of a large amount of heterogeneity does provide support for such. Table 1, Model 2 includes effect size changes in bodyweight (change outcome difference between the intervention and control group) as a single covariate. As can be seen, body weight is a statistically significant covariate for triglycerides. For every 1 kg decrease in bodyweight, an approximate 3 mg/dL decrease in triglycerides can be expected. The adjusted R2 is 76.9%, meaning that 76.9% of the between-study variance (93.7%) is explained by changes in bodyweight while the remaining 23.1% is unexplained. Importantly, the 76.9% and 23.1% sum to 100% because we’re solely concerned here with the variance between studies and not the within-study variability. Additionally, from the output in Table 1, Model 2, a large amount of residual variation is still due to heterogeneity (93.7%) while only 6.3% is attributable to within-sample variability. Thus, while decreases in bodyweight appear to be a strong predictor of decreases in triglycerides, a large amount of between-study heterogeneity continues to exist. This suggests that other covariates are also contributing to between-study heterogeneity. This occurrence is not uncommon in meta-analysis[13]. To address this issue, a radically different approach has recently been proposed in which a formal process for soliciting opinions is sought from quantitatively trained assessors regarding internal biases and subject-matter specialists regarding external biases[21,22]. After adjusting for these biases, the authors reported no apparent heterogeneity[21].
| Variable | Studies (n) | Participants (n) | β | σ | z | p(z) | 95% CI | τ2 | I2res |
| Model 1 (intercept-only) | |||||||||
| Intercept | 6 | 559 | -9.4 | 3.7 | -2.5 | 0.01 | -16.6 to -2.1 | 65.4 | 98.8 |
| Model 2 (intercept + 1 covariate) | |||||||||
| Intercept | 6 | 559 | 7.5 | 5.9 | 1.3 | .02 | -4.1 to 19.1 | ||
| Bodyweight (kg) | 6 | 559 | 2.9 | 0.9 | 3.2 | .001 | 1.1 to 4.8 | 15.1 | 93.7 |
Irrespective of the type of meta-regression model chosen, it’s important to realize that when conducting a meta-analysis, studies are not randomly assigned to covariates[23]. Consequently, meta-regression that includes covariates is considered to be observational in nature and thus, does not support causal inferences. Rather, the validity of these findings would need to be tested in large, well-designed randomized controlled trials.
While the original DerSimonian and Laird random-effects model is the most widely used[11], it may not be the most appropriate. For example, Brockwell et al[24] found that even with large sample sizes, the intervals based on the DerSimonian and Laird method did not attain the preferred coverage for the odds-ratio. This appeared to be the result of the estimated inverse variance weights that included estimates of the variance component. The DerSimonian and Laird approach has also been critiqued by Hardy et al[25]. While not commonly used, DerSimonian et al[26] have recently provided updated random-effects models that they believe are more valid than the original DerSimonian and Laird model. These models include two new two-step methods that appear to approximate the optimal iterative method better than the earlier and most commonly used one-step non-iterative method[11].
Alternative and more computationally intensive parametric random-effects models for estimating between-study heterogeneity in an AD meta-analysis have been proposed. These include, but are not necessarily limited to, maximum likelihood, restricted maximum likelihood and profile likelihood[10,25,27]. One nonparametric random-effects model, the permutations model, has also been proposed for estimating the between-study variance in an aggregate data meta-analysis[28]. While not discussed further, the empirical Bayes model for estimating τ2 has also been proposed for random-effects meta-analyses[27]. However, the results for such have been mixed[10,29].
As described by others[30], the maximum likelihood model assumes that both the within and between-study effects have normal distributions. The between-studies variance for the log-likelihood function is then solved iteratively. Unfortunately, this model does not always converge, the end result being that estimates are reported as missing. In addition, when the between studies variance is negative, it is set to zero. When this occurs, the model collapses into a fixed-effect model.
Coterminous with the maximum likelihood approach, the restricted maximum likelihood model also follows the same assumptions of normal within and between-study effects. However, unlike the maximum likelihood model, only that portion of the likelihood function that doesn’t change, for example, μ if estimating τ2 is maximized. Another similarity to the maximum likelihood approach is that this method doesn’t always converge, resulting in estimates being reported as missing. In addition, when the between-studies variance is negative, the model collapses into a fixed-effect model.
Thompson et al[10] advocate for the use of a restricted maximum likelihood model but not the maximum likelihood model because the latter does not account for the degrees of freedom employed when estimating the fixed-effect portion of the model. The end result is a smaller and standard errors. This may be particularly relevant when the number of studies included is small, a common occurrence in meta-analysis.
The profile likelihood method also utilizes the same function as the maximum likelihood model. However, unlike the maximum likelihood model, nested iterations that converge to a maximum are used to account for the uncertainty associated with the between studies variance. However, similar to the maximum likelihood and restricted maximum likelihood models, the model doesn’t always converge. Consequently, values not calculated are reported as missing. In addition, the confidence intervals produced by this model are asymmetric.
A nonparametric random-effects approach for estimating between-study heterogeneity is the permutations model described by Follmann et al[28]. By permuting the sign of each observed effect, a dataset of observed study outcomes is generated under the assumption that all true study effects are zero and observed effects are due to random variation. The original DerSimonian and Laird model[11] is then used to estimate an overall effect size for each combination. Based on the distribution of these effect sizes, asymmetric confidence intervals as well as heterogeneity statistics are estimated.
When conducting an AD meta-analysis, one is usually interested in a fast, efficient and accurate way of not only calculating the outcome of interest (intercept-only model) but also the association with one or more predictor variables with the outcome of interest (meta-regression). With the former in mind, the user-written routine metaan[30], developed for use in the general statistics package Stata[20], allows one to conduct random-effects AD meta-analysis using the method of moments, maximum likelihood, restricted maximum likelihood and profile likelihood approaches. In addition, the metareg user-written routine[7], also for Stata[20], allows one to calculate the method of moments, maximum likelihood, restricted maximum likelihood and empirical Baye’s estimate. Comprehensive meta-analysis[31], a statistical software package developed specifically for AD meta-analysis, allows the user to conduct random-effects analysis using the method of moments and maximum likelihood approaches. However, only a single predictor (simple meta-regression) is allowed in each model.
While random-effects models are generally preferred over fixed-effect models, random-effects models also have disadvantages. For example, random effects models assume that study-level effect sizes are sampled from a larger distribution of effect sizes[8]. However, this may not be realistic. In addition, the smaller the number of studies included, the poorer the estimate of , i.e., weaker precision[8]. Unfortunately, to the best of the authors’ knowledge, no definitive cutpoint for what constitutes a small number of studies has been established.
Alternative models to both fixed and random-effects meta-analysis for aggregate data have recently been proposed. For example, Bonett et al[32-34] has advocated for what is known as the varying coefficient model. As described by Krizan et al[35], Bonett argues that current fixed-effect models inappropriately assume a common effect size across all included studies and perform poorly when heterogeneity exists while current random-effects models require unrealistic assumptions about random sampling of observed effect sizes from a normally distributed “superpopulation”. In contrast, the varying coefficient model makes no assumptions with respect to a common effect size or random sampling of study populations from a normally distributed, well-defined “superpopulation” of studies. The varying coefficient model has been shown to have better coverage probabilities than both fixed and selected random-effects models when applied across a variety of statistics[32-34], including unstandardized and standardized mean differences[32]. Other alternative models have also been recently proposed by Kulinskaya et al[36].
In time, it is likely that the DerSimonian et al[11] approach will be replaced by more accurate and precise models. However, at this time, it is probably imprudent to over-react to newly proposed models. This is especially true since many of the alternatives proposed as a means of dealing with specific problems in meta-analysis may turn out to have problems of their own, often with substantially worse impact than the problems they were intended to solve. In addition, the usually minor differences in results from the use of different random-effects approaches for meta-analysis may have little effect on the “big picture”, something that should be considered as practically relevant. The former notwithstanding, a need exists for extensive testing of all current models as well as the development of newer ones across a variety of different scenarios. In addition, a gap exists between the development and testing of these models and their timely integration into traditional as well as meta-analytic-specific software packages, one or both of which are probably used by the vast majority of those conducting meta-analytic research. However, from our perspective, the final decision about when a model is ready for widespread use is truly Solomonic.
Peer reviewer: Martin Voracek, Associate Professor, School of Psychology, University of Vienna, Liebiggasse 5, Rm 03-46, Vienna A-1010, Austria
S- Editor Xiong L L- Editor A E- Editor Xiong L
| 1. | Riley RD, Lambert PC, Abo-Zaid G. Meta-analysis of individual participant data: rationale, conduct, and reporting. BMJ. 2010;340:c221. [PubMed] |
| 2. | Glass GV, McGaw B, Smith ML. Meta-analysis in social research. Newbury Park, CA: Sage 1981; 22-23. |
| 3. | Smith ML, Glass GV. Meta-analysis of psychotherapy outcome studies. Am Psychol. 1977;32:752-760. [PubMed] |
| 4. | Olkin I, Sampson A. Comparison of meta-analysis versus analysis of variance of individual patient data. Biometrics. 1998;54:317-322. [PubMed] |
| 5. | Cooper H, Patall EA. The relative benefits of meta-analysis conducted with individual participant data versus aggregated data. Psychol Methods. 2009;14:165-176. [PubMed] |
| 6. | Lipsey MW, Wilson DB. Practical meta-analysis. Thousand Oaks, CA: Sage 2001; 34-72. |
| 8. | Borenstein M, Hedges L, Higgins J, Rothstein H. Introduction to meta-analysis. West Sussex: John Wiley and Sons 2009; 61-62, 83-84. |
| 9. | Hunter JE, Schmidt FL. Fixed effects vs random effects meta-analysis models: implications for cumulative research knowledge. Int J Sel Assess. 2000;8:275-292. [RCA] [DOI] [Full Text] [Cited by in Crossref: 469] [Cited by in RCA: 384] [Article Influence: 22.6] [Reference Citation Analysis (0)] |
| 10. | Thompson SG, Sharp SJ. Explaining heterogeneity in meta-analysis: a comparison of methods. Stat Med. 1999;18:2693-2708. [PubMed] |
| 11. | DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7:177-188. [PubMed] |
| 12. | Dumouchel WH, Harris JE. Bayes methods for combining the results of cancer studies in humans and other species. J Am Stat Assoc. 1983;78:293-308. |
| 13. | Higgins JP, Thompson SG. Quantifying heterogeneity in a meta-analysis. Stat Med. 2002;21:1539-1558. [PubMed] |
| 14. | Higgins JP, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J R Stat Soc Ser A Stat Soc. 2009;172:137-159. [PubMed] |
| 15. | Kelley GA, Kelley KS. Impact of progressive resistance training on lipids and lipoproteins in adults: another look at a meta-analysis using prediction intervals. Prev Med. 2009;49:473-475. [PubMed] |
| 16. | Kelley GA, Kelley KS, Roberts S, Haskell W. Efficacy of aerobic exercise and a prudent diet for improving selected lipids and lipoproteins in adults: a meta-analysis of randomized controlled trials. BMC Med. 2011;9:74. [PubMed] |
| 17. | Sacks HS, Berrier J, Reitman D, Ancona-Berk VA, Chalmers TC. Meta-analyses of randomized controlled trials. N Engl J Med. 1987;316:450-455. [PubMed] |
| 18. | Hedges LV, Pigott TD. The power of statistical tests in meta-analysis. Psychol Methods. 2001;6:203-217. [PubMed] |
| 19. | Higgins JP, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557-560. [PubMed] |
| 20. | Stata/SE for Windows Version 11. 1. version College Station. TX: Stata Corporation 2010; . |
| 21. | Thompson S, Ekelund U, Jebb S, Lindroos AK, Mander A, Sharp S, Turner R, Wilks D. A proposed method of bias adjustment for meta-analyses of published observational studies. Int J Epidemiol. 2011;40:765-777. [PubMed] |
| 22. | Turner RM, Spiegelhalter DJ, Smith GC, Thompson SG. Bias modelling in evidence synthesis. J R Stat Soc Ser A Stat Soc. 2009;172:21-47. [PubMed] |
| 23. | Littell JH, Corcoran J, Pillai V. Systematic reviews and meta-analysis. New York: Oxford University Press 2008; 120. |
| 24. | Brockwell SE, Gordon IR. A comparison of statistical methods for meta-analysis. Stat Med. 2001;20:825-840. [PubMed] |
| 25. | Hardy RJ, Thompson SG. A likelihood approach to meta-analysis with random effects. Stat Med. 1996;15:619-629. [PubMed] |
| 26. | DerSimonian R, Kacker R. Random-effects model for meta-analysis of clinical trials: an update. Contemp Clin Trials. 2007;28:105-114. [PubMed] |
| 27. | Morris CN. Parametric empirical bayes inference - theory and applications. J Am Stat Assoc. 1983;78:47-55. |
| 28. | Follmann DA, Proschan MA. Valid inference in random effects meta-analysis. Biometrics. 1999;55:732-737. [PubMed] |
| 29. | Sidik K, Jonkman JN. A comparison of heterogeneity variance estimators in combining results of studies. Stat Med. 2007;26:1964-1981. [PubMed] |
| 32. | Bonett DG. Meta-analytic interval estimation for standardized and unstandardized mean differences. Psychol Methods. 2009;14:225-238. [PubMed] |
| 33. | Bonett DG. Transforming odds ratios into correlations for meta-analytic research. Am Psychol. 2007;62:254-255. [PubMed] |
| 34. | Bonett DG. Meta-analytic interval estimation for bivariate correlations. Psychol Methods. 2008;13:173-181. [PubMed] |
| 35. | Krizan Z. Synthesizer 1.0: a varying-coefficient meta-analytic tool. Behav Res Methods. 2010;42:863-870. [PubMed] |
| 36. | Kulinskaya E, Morgenthaler S, Staudte RG. Meta Analysis: A Guide to Calibrating and Combining Statistical Evidence. Hoboken, NJ: John Wiley and Sons 2008; 3-14. |