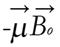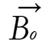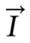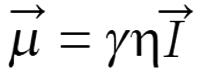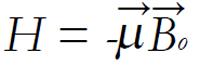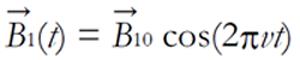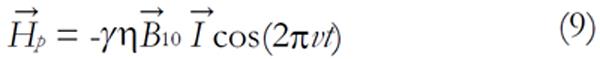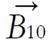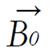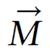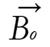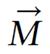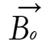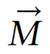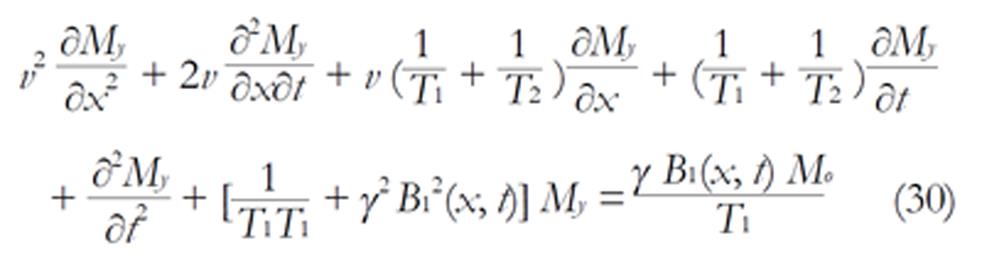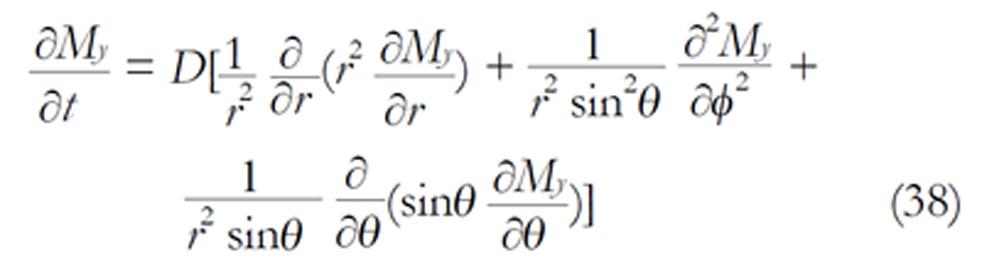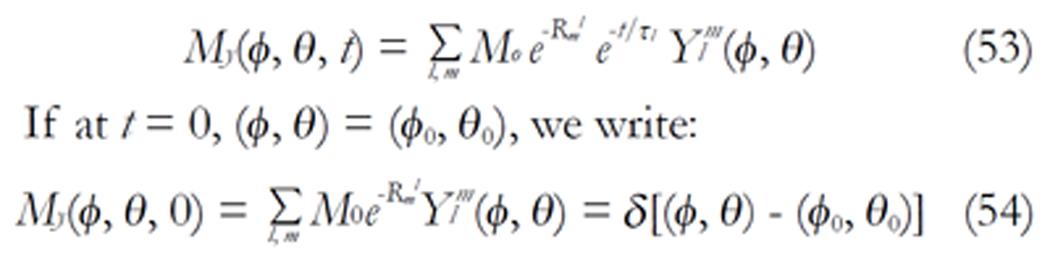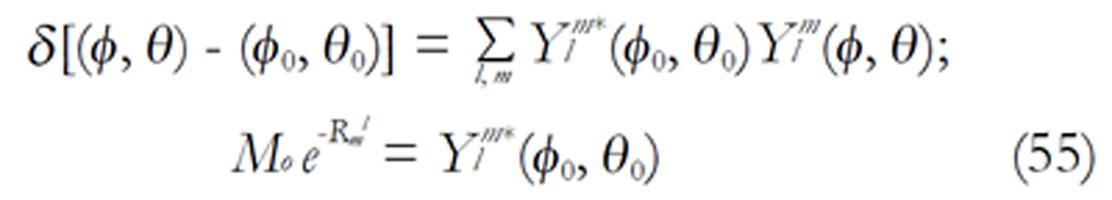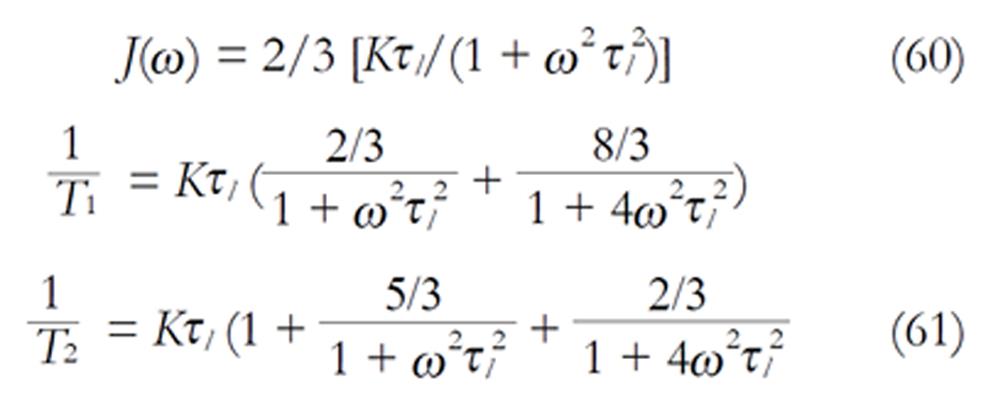Published online Apr 12, 2014. doi: 10.5528/wjtm.v3.i1.17
Revised: February 16, 2014
Accepted: March 3, 2014
Published online: April 12, 2014
Processing time: 189 Days and 11 Hours
Magnetic resonance imaging (MRI), magnetic resonance angiography (MRA) and magnetic resonance spectroscopy (MRS) are fundamental concepts used in modern medicine to improve health care. These concepts are based on the principle of nuclear magnetic resonance (NMR). Over the years, various laboratories around the world have applied different numerical techniques based on the Bloch NMR equations to solve specific problems in physics, biology, chemistry, engineering and medicine. The ultimate goal of any physician is to obtain maximum physical, biophysical, chemical and biological information on any tissue or cell under examination. This goal can be achieved by solving the Bloch NMR flow equations analytically. In this review, we present the basic principle of NMR/MRI in a way that can be easily understood by any researcher who needs an NMR concept to solve a specific medical problems. After a very brief history of the subject, a second order, non homogeneous, time-dependent differential equation derived from the Bloch NMR equation is presented. This equation has the basic intrinsic properties of MRI, MRA and MRS that can be extracted by means of classical and quantum mechanics for possible application in nanomedicine.
Core tip: Magnetic resonance imaging is one of the most powerful methods for investigating structural and dynamics of biological matter. Based on quantum mechanical principles applied to Bloch nuclear magnetic resonance (NMR) flow equations, we aimed to apply the analytical solutions obtained from the Bloch NMR flow equations to nanomedicine. This may trigger research towards the design of nano devices that capable of delivering drugs directly to specifically targeted cells, with the possibility of very early diagnosis of diseases and treating them with powerful drugs at the pathological site alone, reducing any harmful side effects.
- Citation: Onwu OS, Dada OM, Awojoyogbe OB. Physics and mathematics of magnetic resonance imaging for nanomedicine: An overview. World J Transl Med 2014; 3(1): 17-30
- URL: https://www.wjgnet.com/2220-6132/full/v3/i1/17.htm
- DOI: https://dx.doi.org/10.5528/wjtm.v3.i1.17
Nuclear magnetic resonance (NMR) is a very important analytical and experimental tool for physical, chemical and structural analysis of certain organic materials. Magnetic resonance is a branch of spectroscopy that detects the quantum-mechanical transitions induced by electromagnetic (EM) radiation in a system of discrete energy levels of electrons or nuclei placed in a static magnetic field[1,2]. NMR employs EM waves in the radio-frequency range between 900 MHz and 2 KHz. Some nuclei experience nuclear resonance, while others do not. Exhibition of this phenomenon is dependent on whether they possess a property called “spin”[2].
NMR is one of the most powerful methods for investigating the structure and dynamics of matter in different states of aggregation. This is due to the following features: (1) the interactions of nuclear magnetic moments are very weak compared with the thermal energy; therefore, we are dealing with para-magnetism. Moreover, the energy delivered by the radio-frequency generator are much larger compared with the strength of these inter-nuclear couplings. That leads to the possibility of manipulating these interactions in a specific way and simplifying the spectral response; (2) the radio-frequency photons have much lower energy compared with the energy of chemical bonds. Therefore, the interaction of EM radiation with matter, particularly biomolecules, is non-ionizing; and (3) the number of radio-frequency photons with a specific frequency is very large. Hence, the phase of the associated EM wave is very well defined. The high degree of coherence of radio-frequency radiation is essential to implement NMR experiments, including magnetic resonance imaging (MRI)[3].
Spin is a fundamental property of nature, like electrical charge or mass. Spin comes in multiples of 1/2 and can be positive (+) or negative (-). Protons, electrons and neutrons possess spins. Individual unpaired electrons, protons and neutrons each possess a spin of 1/2. In the deuterium atom (2H), for example, with one unpaired electron, one unpaired proton and one unpaired neutron, the total electronic spin is equal to 1/2 and the total nuclear spin is equal to 1. Two or more particles with spins having opposite signs can pair up to eliminate the observable manifestations of spin. An example is helium, (24He). In NMR, it is the unpaired nuclear spins that are important. When placed in a magnetic field of strength B, a particle with a net spin can absorb a photon, of frequency ω. The frequency of ω depends on the gyromagnetic ratio γ, of the particle [as shown in equation (1)], given by the expression:
ω = γB (1)
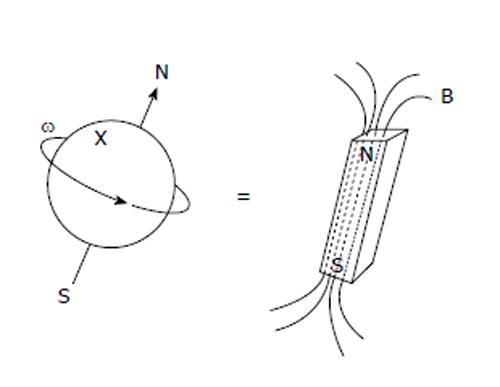
For hydrogen nuclei, the gyromagnetic ratio γ = 42.58 MHz/T[4]. Nuclei are composed of positively charged protons and uncharged neutrons held together by nuclear forces[4,5], as shown in Figure 1.
The shell model for the nucleus tells us that nucleons, just like electrons, fill orbitals. When the number of protons or neutrons equals 2, 8, 20, 28, 50, 82 and 126, the orbitals are filled, because nucleons have spin, just like electrons do, and their spins can pair up when the orbitals are being filled and cancel out. Almost every element in the periodic table has an isotope with a non-zero nuclear spin[4,5]. NMR can only be performed on isotopes whose natural abundance is high enough to be detected; some of the nuclei that are of interest in NMR/MRI are listed in Table 1.
| Nucleus | Spin quantum number (I) | Natural abundance (%) | Gyromagnetic ratioγ(10-7 rad/T sec) | Sensitivity1 (% vs1H) | Electric quadruple moment (Q) (e.1024 cm2) |
| 1H | 1/2 | 99.9844 | 26.7520 | 100.000 | - |
| 2H | 1/1 | 0.0156 | 4.1067 | 0.965 | 0.00277 |
| 13C | 1/2 | 1.1080 | 6.7265 | 1.590 | - |
| 15N | 1/2 | 0.3650 | -2.7108 | 0.104 | - |
| 19F | 1/2 | 100.0000 | 25.167 | 83.300 | - |
| 31P | 1/2 | 100.0000 | 10.829 | 6.630 | - |
We have seen that ω = γB and hence the energy of the radio waves needed to cause a transition between the two spin states is given by equation (2):
E = ηγB (2)
When the energy of the photon matches the energy difference between the two spin states, absorption of energy occurs. In an NMR experiment, the frequency of the photon is in the radio frequency (RF) range. In NMR spectroscopy, ω is between 600 and 800 MHz for hydrogen nuclei. However, in clinical MRI, ω is typically between 15 and 80 MHz for hydrogen imaging[6] (Table 2).
| Nuclei | Unpaired protons | Unpaired neutrons | Net spin | γ(MHz/T) |
| 1H | 1 | 0 | 1/2 | 42.58 |
| 2H | 1 | 1 | 1/1 | 6.54 |
| 31P | 1 | 0 | 1/2 | 17.25 |
| 23Na | 1 | 2 | 3/2 | 11.27 |
| 14N | 1 | 1 | 1/1 | 3.08 |
| 13C | 0 | 1 | 1/2 | 10.71 |
| 19F | 1 | 0 | 1/2 | 40.08 |
To get a better understanding of how particles with spin behave under a magnetic field, we consider a proton that has a spin property. If we imagine the spin of this proton as a magnetic moment vector, causing the proton to behave like a tiny magnet with a North and South Poles. When the proton is placed in an external magnetic field, the spin vector of the particle aligns itself with the external field, just like a magnet would. There is a low energy configuration or state where the poles are aligned N-S-N-S and a high energy state N-N-S-S.
This particle can undergo a transition between the two energy states by the absorption of a photon. A particle in the lower energy state absorbs a photon and ends up in the higher energy state. The energy of this photon must exactly match the energy difference between the two states. The energy E, of a photon is related to its frequency ω, by Planck’s constant (η = h/2π, h = 6.626 × 10-34 Js).
E = ηω (3)
In NMR and MRI, the quantity ω is called the resonance frequency or the Larmor Frequency[6].
MRI is an imaging technique used primarily in medical settings to produce high quality images of the inside of the human body. MRI is based on the principles of NMR, a spectroscopic technique used by scientists to obtain microscopic chemical and physical information about molecules. The technique was called MRI rather than nuclear MRI because of the negative connotations associated with the word nuclear in the late 1970’s. MRI started as a tomographic imaging technique; that is, it produced an image of the NMR signal in a thin slice through the human body. MRI has advanced from a tomographic imaging technique to a volume imaging technique. MRI is based on the absorption and emission of energy in the RF range of the EM spectrum[3,7].
In the past, many scientists were taught that one cannot obtain an image smaller than the wavelength of the energy being used to image it. MRI gets around this limitation by producing images based on spatial variations in the phase and frequency of the RF energy being absorbed and emitted by the imaged object.
Clinical MRI uses the magnetic properties of hydrogen and its interaction with both a large external magnetic field and radio waves to produce highly detailed images of the human body. Hydrogen has a significant magnetic moment and is the most abundant nucleus in the human body. For these reasons, we use only the hydrogen proton in routine clinical imaging[7].
To perform MRI, we first need a strong magnetic field. The field strength of the magnets used for MR is measured in units of Tesla. One (1) Tesla is equal to 10000 Gauss. The magnetic field of the earth is approximately 0.5 Gauss. Given that relationship, a 1.0 T magnet has a magnetic field approximately 20000 times stronger than that of the earth. The type of magnets used for MRI usually belongs to one of three types; permanent, resistive, and superconductive.
A permanent magnet is sometimes referred to as a vertical field magnet. These magnets are constructed of two magnets (one at each pole). The patient lies on a scanning table between these two plates[8].
The advantages of these systems are: relatively low cost, no electricity or cryogenic liquids are needed to maintain the magnetic field, their more open design may help alleviate some patient anxiety and their nearly nonexistent fringe field. It should be noted that not all vertical field magnets are permanent magnets.
Resistive magnets are constructed from a coil of wire. The more turns to the coil, and the more current in the coil, the higher the magnetic field. These types of magnets are most often designed to produce a horizontal field because of their solenoid design. As previously mentioned, some vertical field systems are based on resistive magnets. The main advantages of these types of magnets are: no liquid cryogen, the ability to “turn off” the magnetic field and their relatively small fringe field.
Superconducting magnets are the most common. They are made from coils of wire (as are resistive magnets) and thus produce a horizontal field. They use liquid helium to keep the magnet wire at 4 degrees Kelvin where there is no resistance. The current flows through the wire without having to be connected to an external power source. The main advantage of superconducting magnets is their ability to attain field strengths of up to 3 Tesla for clinical imagers and up to 10 Tesla or more for small bore spectroscopy magnets[9].
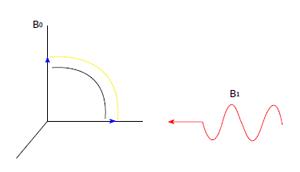
A radio wave is actually an oscillating EM field. The RF field is also referred to as the B1 field. It is oriented perpendicular to the main magnetic field (B0). If we apply a pulse of RF energy into the tissue at the Larmor frequency, we first find the individual spins begin to precess in phase, as will the net magnetization vector. As the RF pulse continues, some of the spins in the lower energy state absorb energy from the RF field and make a transition into the higher energy state. This has the effect of “tipping” the net magnetization toward the transverse plane. This phenomenon is illustrated in Figure 2. For the purpose of this explanation, we will assume sufficient energy is applied to produce a 90-degree flip of the net magnetization. In such an example, it is said that a 90-degree flip angle or a 90-degree pulse has been applied[10].
Oriented perpendicular to B0 is a receiver coil. As the magnetization (now referred to as transverse magnetization, or Mxy) precesses through the receiver coil, a current or signal is induced in the coil. The principle behind this signal induction is Faraday’s Law of Induction. This states that if a magnetic field is moved through a conductor, a current will be produced in the conductor. If we increase the size of the magnetic field, or increase the speed with which it moves, we will increase the size of the signal (current) induced in the conductor.
To detect the signal produced in the coil, the transmitter must be turned off. When the RF pulse is discontinued, the signal in the coil begins at given amplitude (determined by the amount of magnetization precesssing in the transverse plane (Figure 2) and the precessional frequency) and fades rapidly away. This initial signal is referred to as the Free Induction Decay (FID). The signal fades as the individual spins contributing to the net magnetization lose their phase coherence, making the vector sum equal to zero. At the same time, but independently, some of the spins that had moved into the higher energy state give off their energy to their lattice and return to the lower energy state, causing the net magnetization to re-grow along the z axis. This re-growth occurs at a rate given by the tissue relaxation parameter, known as T1[9,10].
A spin packet is a group of spins experiencing the same magnetic field strength. At any instant in time, the magnetic field caused by the spins in each spin packet can be represented by a magnetization vector;
Math 1
The vector sum of the magnetization vectors from all the spin packets is the net magnetization. Adapting the conventional NMR coordinate system, the external magnetic field and the net magnetization vector at equilibrium are both along the Z axis.
The time constant that describes how Mz returns to its equilibrium value is called the spin lattice relaxation time (T1). The equation governing this behavior as a function of time t after its displacement is:
Mz = Mo (1 - e-t/T1) (4)
At equilibrium, the net magnetization vector lies along the direction of the applied magnetic field Bo and is called the equilibrium magnetization Mo. In this configuration, the Z component of magnetization Mz equals Mo. Mz is referred to as the longitudinal magnetization. There is no transverse (Mx or My) magnetization here.
The resonant frequency of a nucleus is determined by a combination of nuclear characteristics and the strength of the magnetic field. The specific relationship between resonant frequency and the field strength is an inherent characteristic of each nuclide and is generally designated as gyromagnetic ratio γ. The resonant frequency is also known as the Larmor frequency.
The time constant that describes the return to equilibrium of the transverse magnetization, Mxy, is called the spin-spin relaxation time, T2.
Mxy = Mxyo e-t/T2 (5)
T2 is always less than or equal to T1. The net magnetization in the XY plane goes to zero and then the longitudinal magnetization grows in until we have Mo along Z.
If a pulse of RF energy with a frequency corresponding to the nuclear precession rate is applied to a material, some of the energy will be absorbed by the individual nuclei. The absorption of energy by a nucleus flips its alignment away from the direction of the magnetic field. This increased energy places the nucleus in an excited state. In this excited state, the precession is now transformed into a spinning motion of the nucleus around the axis of the magnetic field[1-14].
The history of the development of the concept of NMR started with Felix Bloch at Harvard, and Edward Purcell at Stanford, both of whom were awarded the Nobel Prize in 1952, discovered the magnetic resonance phenomenon independently in 1946, using different instrumentation. In the period between 1950 and 1970, NMR was developed and used for chemical and physical molecular analysis. In 1971 Raymond Damadian (an Armenian-American medical practitioner and inventor of the first MR Scanning Machine) showed that the nuclear magnetic relaxation times of tissues and tumors differed, thus motivating scientists to consider magnetic resonance for the detection of disease. In 1973 the X-ray-based computerized tomography (CT) was introduced by Hounsfield. MRI was first demonstrated on small test tube samples that same year by Paul Lauterbur. He used a technique similar to that used in CT. In 1975 Richard Ernst, a Swiss physical chemist, proposed MRI using phase and frequency encoding, and the Fourier Transform. This technique is the basis of current MRI techniques. A few years later, in 1977, Raymond Damadian demonstrated MRI called field-focusing NMR. In this same year, Peter Mansfield developed the echo-planar imaging (EPI) technique. This technique was later developed to produce images at video rates (30 ms/image). Edelstein and coworkers demonstrated imaging of the body using Ernst’s technique in 1980. A single image could be acquired in approximately five minutes by this technique. By 1986, imaging time was reduced to about five seconds, without sacrificing significant image quality. In the same year, the NMR microscope was developed, which allowed approximately 10m resolution on approximately one cm samples. In 1987 EPI was used to perform real-time moving imaging of a single cardiac cycle. In this same year, Charles Dumoulin perfected magnetic resonance angiography (MRA), which allowed imaging of flowing blood without the use of contrast agents.
In 1991, Richard Ernst was rewarded for his achievements in pulsed Fourier Transform NMR and MRI with the Nobel Prize in Chemistry. In 1992 functional MRI (fMRI) was developed. This technique allows the mapping of the functions of the various regions of the human brain. Five years earlier, many clinicians thought EPI’s primary application was to be in real-time cardiac imaging. The development of fMRI opened up a new application for EPI in mapping the regions of the brain responsible for thought and motor control. In 1994, researchers at the State University of New York at Stony Brook and Princeton University demonstrated the imaging of hyperpolarized 129Xe gas for respiration studies.
In 2003, Paul C Lauterbur of the University of Illinois and Sir Peter Mansfield of the University of Nottingham were awarded the Nobel Prize in Medicine for their discoveries concerning MRI. MRI is clearly a young, but growing science[1,3,5-16].
The appearance of NMR spectra, and consequently the molecular structure they are able to provide, arises from the discrete nature of the energy levels pertaining to a nuclear spin system. The energy levels are mainly a result of Zeeman interaction,
Math 2
between the static magnetic field of induction
Math 3
and nuclear magnetic moment
Math 4
The quantum-mechanical quantity called spin momentum,
Math 5
is related to magnetic moment by
Math 6
where γ is the gyromagnetic ratio and η is the Planck’s constant divided by 2π.
In the absence of the magnetic nuclear, the spin states are generated. The application of a static magnetic field which induces a magnetic interaction, is described by Zeeman Hamiltonian
Math 7
Taking the magnetic field orientation to be along the z-direction we get:
H = -γηBo Iz (6)
The Eigen values Em of this Hamiltonian can be evaluated from the Schrodinger equation
H|m> = -γηB0m|m> (7)
where |m> is the Eigen state corresponding to the Eigen value Em = -γηBom. The magnetic quantum number is m, where m = l, l-1, ... , -l. Therefore, the equidistant energy differences are for the single-quantum transitions m = ±1 given by[1,4,5,7]
ΔE = ηω0 (8)
where the Larmor frequency is defined as[1,4,5,7]
vo = vL = ω0/2π
Another important ingredient for a magnetic resonance experiment is represented by the presence of the RF field. Only the magnetic component of the EM field, i.e.,
Math 8
interacts with the magnetic moment of the nuclei. The amplitude of the RF field is and v is the carrier frequency. This field is produced by an RF coil and leads to a perturbation Hamiltonian:
Math 9
From the time-dependent perturbation theory of quantum mechanics, it can be stated that a transition between two states |ψ> and |> is allowed, provided that <ψ|Hp|> ≠ 0. This takes place if v ≈ v0 (i.e., the resonance condition) and the alternative magnetic field
Math 10
is polarized perpendicular to the static magnetic field[11]
Math 11
In general, NMR experiments are performed at high temperatures, employing a large number of spins. These features lead to the possibility to treat classically some aspects of the experiments. The excess of spins oriented along the static magnetic field
Math 12
with respect to those oriented in the opposite direction results in a macroscopic nuclear magnetization
Math 13
aligned along the static magnetic field, which is called the equilibrium magnetization. It can be displaced from this equilibrium by an appropriate perturbation, for instance, by an RF excitation. It is then subject to a precessional motion around
Math 14
with the Larmor frequency vL. The EM perturbation that brings
Math 15
into a plane perpendicular to
Math 16
allows the observation of the Larmor precession through an electromotive force that occurs in a coil whose axis is contained in that plane. This can be done by rotation of the magnetization using a resonant 90° RF pulse. The nuclear magnetization
Math 17
can be oriented antiparallel to
Math 18
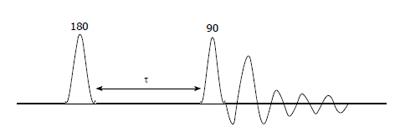
by the action of a 180° pulse. The majority of NMR experiments used pulse sequences composed of 90° and 180° RF pulses[9-18].
A coil of wire placed around the x-axis will provide a magnetic field along the x-axis when a direct current is passed through the coil. An alternating current will produce a magnetic field that alternates in direction. In a frame of reference rotating about the z-axis at a frequency equal to that of the alternating current, the magnetic field along the x’-axis will be constant, just as in the direct current case in the laboratory frame. This is the same as moving the coil about the rotating frame coordinate system at the Larmor Frequency. In magnetic resonance, the magnetic field created by the coil passing an alternating current at the Larmor frequency is called the B1 magnetic field. When the alternating current through the coil is turned on and off it creates a pulsed B1 magnetic field along the x’-axis. The spins respond to this pulse in such a way as to cause the net magnetization vector to rotate about the direction of the applied B1 field. The rotation angle depends on the length of time τ for which the field is switched on and its magnitude, B1[2,6,7,9].
A 90° pulse is one that rotates the magnetization vector clockwise by 90° about the x’-axis and rotates the equilibrium magnetization down to the y’-axis. In the laboratory frame, the equilibrium magnetization spirals down around the z-axis to the xy-plane. One can now see why the rotating frame of reference is helpful in describing the behavior of magnetization in response to a pulsed magnetic field. A 180° pulse will rotate the magnetization vector by 180° and rotates the equilibrium magnetization down along the z-axis.
The net magnetization at any orientation will behave according to the rotation equation. For example, a net magnetization vector along the y’-axis will end up along the y’-axis when acted upon by a 180° pulse of B1 along the x’-axis. A net magnetization vector between x’- and y’- will end up between x’ and y’ after the application of 180° pulse of B1 applied along the x’-axis[9].
Longitudinal magnetization is aligned along the field axis Bo (that is, the z-axis) and has a finite equilibrium value of Moz. Moz represents the equilibrium magnetization at the start of any NMR experiment.
Transverse magnetization is perpendicular to Bo, precesses around the z-axis at the Larmor frequency and has an equilibrium value of zero[13].
ω = 2πv = -γB0
A simple 1D NMR spectrum is obtained by a 90° pulse, followed by detection of the FID and Fourier transformation of the FID. More complicated pulse sequences allow measurement of specific parameters, 2D and multi-dimensional data.
The inversion-recovery (IR) pulse sequence can be used to measure the T1 relaxation times of all the resonances in a spectrum. IR pulse sequence is pictorially represented in Figure 3.
Alternatively, the zero crossing point for each peak can be used to estimate the T1. Using the time τ0 at which the signal I is zero:
τ0 = T1 ln2 = 0.693 T1 (10)
This provides a very useful spot check for the value of T1 in any sample. We must note that the relaxation delay between subsequent scans must be set to at least 5 T1 for experiments for good estimates of T1.
The saturation-recovery pulse sequence starts from perfectly equal populations of α and β spin states (Mz = 0, achievable by saturation). During a subsequent waiting period t, the z-magnetization reappears in an exponential recovery until it has assumed equilibrium value Mzo for a very long time t:
Mz = Mzo (1 - e-t/T1) (11)
An experiment of this nature does not require long recovery delays between scans; however, saturation of the spin states is not always easy[10].
Any pulsed NMR experiment is repeated many times, and the scans added together to improve signal-to-noise (S/N) ratio. If the signals are not fully relaxed before each pulse/acquisition, then the signal in each scan will progressively decrease.
A recovery delay of about 5 × T1 between subsequent scans almost completely restores Mzo, yielding reliable integrals. Recovery delays of about 1.4 T1 maximizes S/N ratio, but the integrals of slowly relaxing signals will be smaller than those of the rapidly relaxing signals.
If a signal, or a whole spectrum, is irradiated continuously with RF, then the populations Nα and Nβ will equalize and no signal can be observed. This can be used for selective removal of a peak, e.g., a solvent peak from a spectrum. For example, in biological samples, H2O would yield a huge signal without solvent suppression. A simple way of solvent suppression is presented by selective saturation by pre-irradiation = weak irradiation of the solvent signal during the recovery delay before the 90° pulse[10,18].
Weak interactions between the small magnetic moments of nuclear spins with the environment result in slow relaxation rates and allow the design of long and complicated pulse sequences. In contrast to optical spectroscopy, nuclear spins can access only a finite number of energy levels. This allows the accurate calculation of the outcome of pulse sequences. Transverse magnetization can be destroyed by a “pulsed field gradient”: an electric current is sent through a gradient coil for a few milliseconds. This results in a wide distribution of Larmor frequencies during the gradient and, hence, averaging of the transverse magnetization vectors to zero[18].
The energy of the magnetic moment of a nuclear spin in a magnetic field is given by
E = -μB (12)
where μ is the spin angular momentum and B is the magnetic field (in general B is a vector quantity). To conduct an NMR experiment, a sample is first placed in a static field. By convention, the direction of the static magnetic field is along the z-axis, and the magnitude of the magnetic field is given by Bo (no longer a vector because it points only along the z-axis). In this case, the energy of a nuclear spin in an NMR magnet becomes
E = -μzB0 = -γIzBo (13)
where γ is the gyromagnetic ratio (sometimes called the magnetogyric ratio) and Iz is the spin quantum number in the z-axis direction. The energy associated with a particular quantum number m is given as:
Em = -mηγBo (14)
NMR transition energies are very small. These small energies translate into low sensitivity. When samples are placed into a magnetic field, a small excess of nuclei fall into the α state. This excess of spins in the α over the β states accounts for the entire net magnetization that is used in the NMR experiment. The ratio of the number of spins in the β state to those in the α state is given by a Boltzmann distribution:
Nα/Nβ = eΔE/(kBT) (15)
where ΔE is the difference of energies of the α and β states, kB is Boltzmann constant, and T is the absolute temperature. Higher magnetic fields produce correspondingly larger differences in spin states, leading to greater sensitivity[12,14,15].
If the bulk magnetization is along the field direction, as it is at equilibrium, then there is no torque and hence no motion. As expected, at equilibrium the system is stationary. If the system is away from equilibrium and the bulk magnetization vector is oriented other than along the z-axis, then the magnetization precesses (rotates) about the z-axis with an angular velocity given by the energy separation of the two states (γBo). This torque will not change the length of the magnetization vector; it only varies its orientation. This orientation cannot be the only motion, since the system would never return to equilibrium. Therefore, along with the rotation, there is a relaxation of the vector to bring it back along the z-axis. Therefore the x- and y-components of the nuclear magnetization decay towards zero, and the z-component decays towards the equilibrium value (Mo)[4,10,14].
Considering bulk magnetization M that arises from all the magnetic moments in a sample, M experiences a torque when placed in a magnetic field, according to the expression given below:
dJ(t)/dt = M(t) ×B(t) (16)
where J(t) is the bulk spin angular momentum. The vector quantities in equation (16) are time dependent. The time-dependence of the magnetic field comes about when we apply RF pulses along the x- or y-axis. Equation (16) is essentially identical to an equation that describes the motion of a gyroscope[18-20]:
dL(t)/dt = r×mg (17)
where L(t) is the gyroscope’s angular momentum, r the radius from the fixed point of rotation, m is the mass, and g is gravity. Thus, a nuclear spin in a magnetic field will behave much like a gyroscope in a gravitational field. To make equation (16) useful, we use the relationship for the z-component of the magnetic moment:
μz = γIz = γηm (18)
Then multiply each side by γ to yield
dM(t)/dt = M(t) ×γB(t) (19)
In 1946 Felix Bloch formulated a set of equations that describe the behavior of nuclear spin in a magnetic field under the influence of RF pulses. He modified equation (19), given above, to account for the observation that nuclear spins “relax” to equilibrium values following the application of RF pulses. Bloch assumed they relax along the z-axis and in the x-y plane at different rates, but following first order kinetics. These rates are designated 1/T1 and 1/T2 for the z-axis and x-y plane, respectively. T1 is called spin-lattice relaxation and T2 the spin-spin relaxation. With the addition of relaxation, equation (19) becomes:
dM(t)/dt = M(t) ×γB(t) - R [M(t) - Mo] (20)
where R is the “relaxation matrix”. Equation (20) can best be explained by considering each of its components:
dMz(t)/dt = γ[Mx(t) By(t) ×My(t) Bx(t)] - [Mz(t) - Mo]/T1
dMx(t)/dt = γ[My(t) Bz(t) ×Mz(t) By(t)] - Mx(t)/T2
dMy(t)/dt = γ[Mz(t) Bx(t) ×Mx(t) Bz(t)] - My(t)/T2 (21)
The terms in equation (21) that do not involve either T1 or T2 are the result of the cross product in equation (20). Equation (21) describes the motion of magnetization in the “laboratory frame”, an ordinary coordinate is stationary. Mathematically, the laboratory frame is not the simplest coordinate system, because the magnetization is moving at a frequency ω0 = γBo in the x-y (transverse) plane. A simpler coordinate system is the “rotating frame”, in which the x-y plane rotates around the z-axis at a frequency Ω = -γBo. In the rotating frame, magnetization “on resonance” does not precess in the transverse plane. The transformation of equation (21) to the rotating frame is achieved by replacing each Bz (defined as Bo) by Ω/λ:
dMz(t)/dt = γ [Mx(t) Byr(t) - My(t) Bxr(t)] - [Mz(t) - Mo]/T1
dMx(t)/dt = -ΩMy(t) - γMz(t) Byr(t) - Mx(t)/T2
dMy(t)/dt = γMz(t) Bxr(t) + ΩMx(t) - My(t)/T2 (22)
In equation (22), the components of B have been written with r superscripts to denote that it is a rotating frame[17-23].
We shall examine the behavior of equation (22) under two different limiting conditions, the effect of a short RF pulse and free precession. The RF pulse will be assumed to be very short compared to either relaxation times T1 and T2, as well as the angular frequency Ω. This assumption is valid for many typical pulsed NMR experiments, in which the pulse lengths can be as short as 5 μs. If the RF pulse is applied along the x-axis, these conditions will allow us to neglect terms in equation (22) that contain T1, T2, Ω, and By.
dMz/dt = -My(t) γBxr(t)
dMx(t)/dt = 0
dMy(t)/dt = Mz(t) γBxr(t) (23)
Before solving equation (23), we need to discuss the meaning of Bx(t) and By(t). We can recall that Bo is the static magnetic field strength oriented along the z-axis. Bx(t) and By(t) are magnetic fields oriented along the x- and y-axes that are generated by rf pulses. By analogy to ω0 = γBo defining the frequency of the NMR transitions in the static magnetic field, we can see that the terms γBx(t) and γBy(t) are frequencies of the magnetization rotating around the x- or y-axis. Thus, applying these frequencies for different periods of time will allow for different degrees of rotation around the x- or y-axis. If we introduce a frequency of rotation about the x-axis as ωx = γBx(t), solutions to equation (23) can now be given as:
Mz(t) = Mo cos(ωxt)
Mx(t) = 0
My(t) = Mo sin(ωxt) (24)
Finally, if we let θ = ωxt be the pulse angle, equation (24) shows that application of a magnetic field (RF pulse) along the x-axis causes the magnetization that was originally along the z-axis to rotate toward the y-axis by an angle θ. Note that when θ = 0, Mz(t) = Mo and MY(t) = 0 (all the magnetization is still pointing along the z-axis). When θ = 90°, MY(t) = Mo and Mz(t) = 0 (all the magnetization is still pointing along the y-axis). These have described the effects of a simple RF pulse. The second limiting condition for equation (22) is free precession in the absence of any applied pulse. In that case, Bx and By are both equal to zero, and equation (22) becomes:
dMz(t)/dt = -[Mz(t) - Mo]/T1
dMx(t)/dt = -ΩMy(t) - Mx(t)/T2
dMy(t)/dt = -ΩMx(t) - My(t)/T2 (25)
The solutions to equation (25) can be given as:
Mz(t) = Mo (1 - et/T1)
Mx(t) = Mo cos(Ωt) e-t/T2
My(t) = Mo sin(Ωt) et/T2 (26)
Equation (26) describes magnetization precessing in the x-y plane at a frequency Ω, while it is relaxing along the z-axis at a rate of 1/T1 and relaxing in the x-y plane at a rate 1/T2[17-19,21,24].
The Bloch NMR flow equations can be written as[25,26]:
∂Mx/∂t + v ∂Mx/∂x = -Mx/T2 (27)
∂My/∂t + v ∂My/∂x = γMzB1(x) - My/T2 (28)
∂Mz/∂t + v ∂Mz/∂x = -γMzB1(x) + (Mo - Mz)/T1 (29)
From equation (28 and 29), we have
Math 19
Equation (30) is a general second order, non-homogeneous, time dependent differential equation that can be applied to any fluid flow problem. At any given time t, we can obtain information about the system, provided that appropriate boundary conditions are applied. From equation (30), we can obtain the diffusion equation, the wave equation, telephone and telegraph equations, Schrödinger’s equation, Legendre’s equation, etc., and solve them in terms of NMR parameters by the application of appropriate initial or boundary conditions. Hence, we can obtain very important information about the dynamics of the system. It should be noted, however, that the term FoγB1(x, t) is the forcing function (Fo = Mo/T1). If the function is zero, we have a freely vibrating system; otherwise, the system is undergoing a forced vibration.
A diffusion equation can easily be obtained from equation (30) if we assume that the NMR wave is a plane wave such that:
My(x, t) = A eμx + ηt (31)
subject to the following MRI experimental conditions:
γ2B12(x, t) << 1/(T1T2) (32)
where μ and η are dependent on the NMR parameters. Taking
η2 = Tg and 2η = T0 (33)
Equation (30) becomes
v2 ∂2My/∂x2 + T0 ∂My/∂t = FoγB1(x, t) (34)
If we write
D = -v2/T0
v = (-D T0)1/2 (35)
Then equation (34) becomes
∂My/∂t = D ∂2My/∂x2 + Fo/T0γB1(x, t) (36a)
Equation (36a) can be written in generalized co-ordinates as:
∂My/∂t = D∂2My + Fo/T0γB1(t) (36b)
If D represents the diffusion coefficient, then Equation (36) is the equation of diffusion of magnetization as the nuclear spins move. The function Fo/T0γB1(x, t) is the forcing function, which shows that application of the RF B1 field has an influence on the diffusion of magnetization within a voxel. It is interesting to note that the dimension of equation (35) exactly matches that of the diffusion coefficient.
Equation (36) is only applicable when D is non-directional. That is, we have a constant diffusion coefficient (isotropic medium). Equation (36) can be considered for restricted diffusion in various geometries[25,26]. This model would work quite well for molecules that move very short distances over a very considerable amount of time; where
Ω = Tg + γ2B12(x, t);
Fo = Mo/T1;
Tg = 1/(T1T2)
and T0 = 1/T1 + 1/T2 (37)
where γ is the gyromagnetic ratio, D is the diffusion coefficient, v is the fluid velocity, T1 is the spin lattice relaxation time, T2 is the spin relaxation time, Mo is the equilibrium magnetization, B1(x, t) is the applied magnetic field and My is the transverse magnetization. Solutions to equation (36) have been discussed by applying a number of analytical methods[26], and for the present purpose it is sufficient to design the NMR system in such a way that the transverse magnetization My, takes the form of a plane wave.
The random re-orientation of molecules (or larger systems) is an important process for many biophysical probes. By the equipartition theorem, larger molecules re-orient more slowly than do smaller objects and, hence, measurements of the rotational diffusion constants can give insight into the overall mass and its distribution within an object. In this study, the mathematical concept of rotational diffusion MRI and molecular dynamics of biological fluids is presented. This approach ensures the analytical solution of the Bloch NMR flow equation, which enables us to obtain the NMR transverse magnetization in terms of spherical harmonic functions and NMR relaxation parameters for measuring rotational diffusion at the molecular level.
Theoretical and experimental studies to determine rotational diffusion coefficients using Fluorescence Correlation Spectroscopy, fluorescence anisotropy, flow birefringence, dielectric spectroscopy, NMR relaxation and other biophysical methods that are sensitive to picosecond or slower rotational processes have been published earlier studies[1-12].
In this study, we have presented a new method based on the Bloch NMR flow equation to measure rotational diffusion of biological fluids. The approach ensures that analytical solutions to the Bloch NMR flow equation yield the NMR transverse magnetization in terms of spherical harmonic functions and NMR relaxation parameters. The NMR/MRI technique can generate exquisite images of the soft tissue anatomy of the human body; therefore, this method is expected to become an efficient and reliable technique for measuring rotational diffusion at the molecular level for application in nanomedicine.
We consider a tumbling molecule that can be completely described by a rotational diffusion equation where the radius is fixed (r = R). It would be very important to derive the diffusion system directly from equations (36). Equations (36) within a spherical cavity is given by
Math 20
A tumbling molecule exhibits rotational diffusion that describes the tumbling motion of the molecules. In this case, the radius is fixed (r = R) and equation (38) becomes the rotational diffusion equation (the radial differential terms disappear):
Math 21
where Dr = D/R2 is the rotational diffusion coefficient and R is the fixed radius of a sphere. The parameter D is called translational diffusion coefficient. The NMR transverse magnetization My of the diffusing molecule which is making a tumbling motion is the general solution of equation (39) obtained by the method of separation of variables:
My(φ, θ, t) = A e-Dr l (l + 1) tYlm(φ, θ) (40)
Equation (40) can be related to the correlation time constant τ:
1/τ1 = D/R2l (l + 1) = Dr l (l + 1) (41)
Equation (40) becomes:
My(φ, θ, t) = A e-t/τlYlm(φ, θ) (42)
If we sum over all possible values of m and l, equation (42) gives
Math 22
The rotational correlation time τl , is the characteristic time constant associated with the Brownian rotation diffusion of a particle in a solution. This is the time it takes the particle to rotate by one radian and it is a function of the particle size. For globular proteins, a spherical approximation can be used and the rotational correlation time is given by equation (44)[21]
τl = 4πηR3/(3kT) (44)
where η is the viscosity of the solvent, R is the effective hydrodynamic radius of the protein molecule, k is the Boltzmann constant and T is the temperature. From the molecular weight (MW) of the protein (M), the hydrodynamic radius can be calculated as follows:
R = [3M/(4πρNa)]1/3 + Rw (45)
where ρ is the average density for proteins (1.37 g/cm3), Na is the Avogadro’s number and rw is the hydration radius (1.6Ǻ to 3.2Ǻ). For rigid protein molecules, in the limit of slow molecular motion (τl >> 0.5 ns) and high magnetic field (500 MHz or greater), a closed-form solution for τl as a function of the ratio of the longitudinal (T1) and transverse (T2) 15N relaxation times is
τl = 1/(4πωN) (6T1/T2 - 7)1/2 (46a)
where ωN is the 15N resonance frequency (Hz). Average 15N T1 and T2 relaxation times for a given protein can be measured using 1D 15N-edited relaxation experiments. To minimize contributions from unfolded segments, each 1D spectrum is integrated over the downfield backbone amide 1H region (typically 10.5 to 8.5 ppm) and the results are used to fit an exponential decay as a function of delay time. One then computes the correlation time and compares it to a standard curve of τl vs protein MW obtained at the same temperature on a series of known monomeric proteins of varying size. The T1/T2 method is suitable for proteins with MW of up to MW ≈ 25 kDa. Accurate measurement of the diminishing 15N T2 becomes difficult for larger proteins and cross-correlated relaxation rates are measured instead[21].
The parameter l is a dimensionless constant; therefore, it may be appropriate in this study to define l as
l = T1/T2 (46b)
Values of rotational correlated time for some monomeric NESG (North East Structural Genomics Consortium) targets are shown in Table 1.
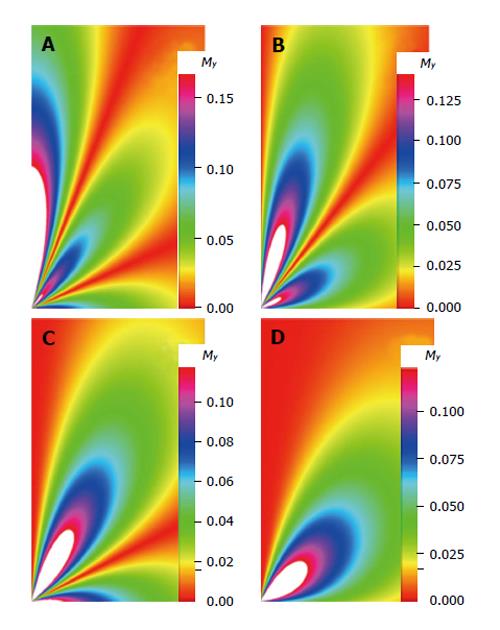
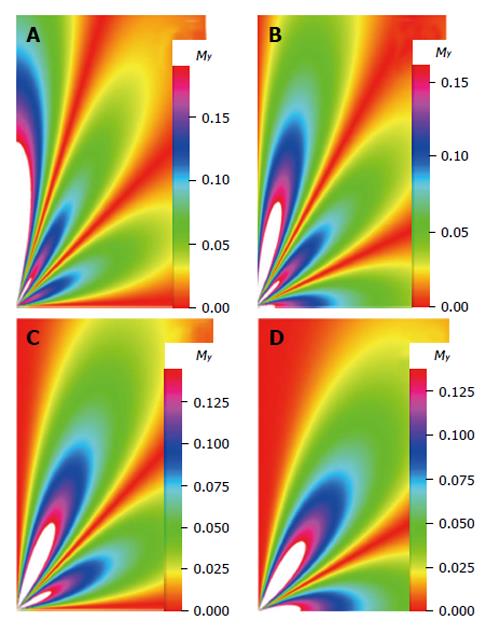
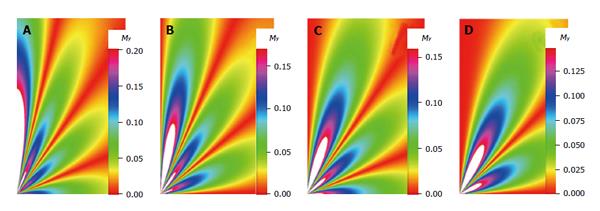
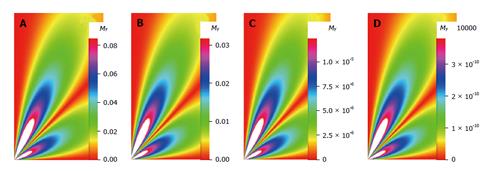
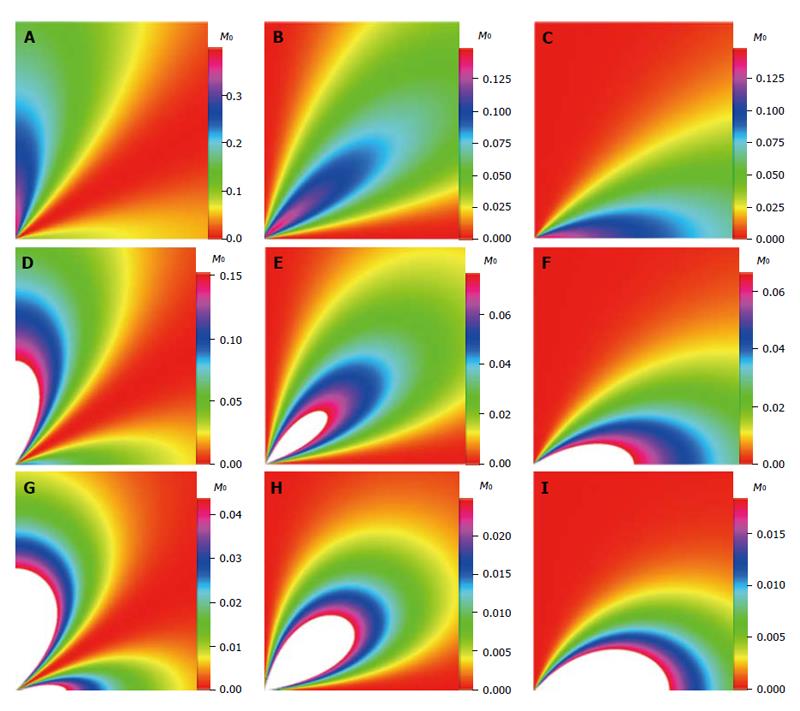
The density images below are obtained for the first three isotopes of Table 3, for M0 = 1, m = 0, 1, 2, 3, and a time of 3 ns. The plots shown in Figures 4, 5, 6, and 7 are made with the assumption that the spins move across rigid spheres whose radii (= R) are in the range {0, 81/2}. Figures 4-7 give the density mapping of the transverse magnetization for specific correlation times (i.e., for selected NESG targets) and NMR relaxation parameters.
| NESG target (isotope labeling) | MW (kDa) | 15N T1 (ms) | 15N T2 (ms) | l = T1/T2 | τl(ns) |
| PsR76A (NC5) | 7.2 | 478 | 128 | 3.734375 | 5.1 |
| VfR117 (NC) | 11.2 | 605 | 119 | 5.084034 | 6.3 |
| SyR11 (NC5) | 12.4 | 630 | 104 | 6.057692 | 7.1 |
| ER541-37-162 (NC5) | 15.8 | 729 | 66.5 | 10.96241 | 10.0 |
| ER540 (NC5) | 18.8 | 909 | 66.5 | 13.66917 | 11.3 |
| SoR190 (NC) | 13.8 | 697.5 | 100.9 | 6.912785 | 7.7 |
| TR80 (NC5) | 10.5 | 612.8 | 102.9 | 5.955296 | 7.0 |
| Ubiquitin (NC) | 9 | 441.8 | 144.6 | 3.055325 | 4.4 |
| HR2873B (NC) | 10.7 | 492 | 115 | 4.278261 | 5.7 |
| B-domain (NC) | 7.2 | 423.5 | 153.3 | 2.762557 | 4.05 |
| BcR97A (NC) | 13.1 | 705.8 | 80.6 | 8.756824 | 8.8 |
| PfR193A (NC) | 13.6 | 733.9 | 80.9 | 9.071693 | 9.0 |
| MvR76 (NC) | 20.2 | 1015 | 64.5 | 15.73643 | 12.2 |
| DvR115G (NC) | 10.9 | 608.7 | 115.6 | 5.265571 | 6.5 |
| MrR110B (NC5) | 11.8 | 707 | 99.2 | 7.127016 | 7.8 |
| VpR247 (NC5) | 12.5 | 661.2 | 88.3 | 7.488109 | 8.05 |
| BcR147A (NC) | 11.9 | 645 | 104 | 6.201923 | 7.2 |
| WR73 (NC5) | 21.9 | 1261 | 41.3 | 30.53269 | 13.0 |
| NsR431C (NC5) | 16.8 | 855.5 | 71.2 | 12.01545 | 10.6 |
| StR82 (NC) | 9.2 | 537.3 | 100.4 | 5.351594 | 6.6 |
When a particle moves in a fluid, either under the influence of an applied force or torque, or due to Brownian motion, it experiences frictional resistance. The proportionality between particle velocity and frictional resistance is the frictional coefficient.
It may be significant to note that the rotational diffusion coefficient Dr, can be defined from equation (39) as
Dr = D/R2 = kB T/(R2fr) (47)
where kB is the Boltzmann’s constant, fr is the rotational frictional coefficient, R is the hydrodynamic radius of the molecule being observed and T is the absolute temperature. Equation (47) becomes discretized when the time constant is introduced:
1/τl = kB T/(R2fr) l (l + 1) (48)
fr = kB Tτl/R2l (l + 1) (49)
Therefore, for the NESG target PsR76A (NC5)[21], the rotational friction coefficient can easily be calculated:
fr = 90.16765 × 10-9kBT/R2
It may be very important to note from equations (35, 39) that
D = -v2/T0 = Dr R2 (50a)
And
Dr = -v2/(T0R2) = -ω2/T0 (50b)
where
ω = v/R
is the angular velocity. Hence, we have:
fr = kB T T0/v2 (50c)
The angular drift velocity can be defined as
Ωd = dω/dT0 = Fω/fr (51)
Equation (50b) defines the angular deviation in terms of the T1 and T2 relaxation parameters for rotational diffusion about a single axis
ω2 = DrT0 (52)
Equation (52) describes the response of the angular drift velocity to an external torque Fω assuming that the flow stays non-turbulent and that inertial effects can be neglected.
Rotational diffusion is a process by which the equilibrium statistical distribution of the overall orientation of molecules is maintained or restored. The random re-orientation of molecules is an important process for many biophysical probes. The rotational diffusion of molecules in the presence of static magnetic and RF fields can be described by the NMR diffusion equation. The NMR diffusion equation within a spherical cavity has been described in equation (42).
The radial parameter R is constant; therefore, we may assume that A = Mo e-R. If we sum over all m and l, we have:
Math 23
Then, the delta function may be expanded such that:
Math 24
For this system, the autocorrelation function may be given as:
G(t) = 12π/20 [μ0/(4π)]2η2γ4/r6
[Y2m*(φ, θ) Y2m(φ, θ)e-t/τl] (57)
The angle bracket is the average over the transverse magnetization of the rotating molecules. This average is given as:
1/4∫d(φ, θ)∫d(φ0, θ0)Yln*(φ0, θ0) Ylm(φ, θ)
Y2m(0, θ0) Y2m*(, θ)e-t/τl (58)
If we perform the integral, we obtain[27-31]:
G(t) = K/3 e-t/τl (59)
where τl = R2/(6D) = 1/(6Dr), and K = 9/20 [μ0/(4π)]2η2γ4/r6 is the second moment of interaction and r is the separation between two nuclear spins. The spectral density function is the Fourier transformation[27-31] of equation (53):
Math 25
From equation (55), we can map Mo as a function of the radius of the rigid rotator R (which is also dependent on θ0 and φ0). At the point when RF B1 field is just removed, Mo starts building up from its lowest value. For multi-voxel imaging, R may be changing with different tissue conditions. This may have very important influence on the changes in Mo. Figure 8 show the changes in Mo with assumed ranges for R.
We have presented the basic principle of NMR/MRI in a way that can be easily understood and that may fascinate researchers into the field of NMR/MRI. After a very brief history of the subject, a second order non-homogeneous, time dependent differential equation derived from the Bloch NMR equation was presented. Note that equation (30) uniquely assembles all the NMR, MRI, MRA and magnetic resonance spectroscopy parameters in an exciting way ready to be explored. The NMR signals as represented by equations (40-42) and Figures 4-7 are greatly influenced by the T1 and T2 relation times and the NMR parameter m. As l increases the motion gets faster and as m is increased, the particle’s motion moves closer to orbiting the equator. This can greatly motivate further research into the use of rotational motion of nanoparticles to perform medical procedures inside the human body, noninvasively. Equations (40-42) are also the solutions for a rigidly rotating diatomic molecule. They are the angular parts of the hydrogen atom wave functions. These functions are important in many theoretical and practical applications, particularly in the computation of atomic orbital electron configurations, representation of gravitational fields, geoids, and the magnetic fields of planetary bodies and stars, and characterization of the cosmic microwave background radiation. In 3D computer graphics, spherical harmonics play a special role in a wide variety of topics including indirect lighting (ambient occlusion, global illumination, pre computed radiance transfer, etc.) and recognition of 3D shapes. The concept presented in this study can also be used to analyze the Earth’s magnetic resonance. Application of this concept to nanomedicine will be the focus of our next investigation. Towards this goal, we derived the standard parameters of NMR relaxometry of diatomic molecules directly from the NMR diffusion equation. The advantage of this is that we are able to obtain the autocorrelation function and the spectral density function without the use of the rigorous method of probability distribution function.
P- Reviewer: Sijens PE S- Editor: Song XX L- Editor: Stewart G E- Editor: Liu SQ
| 1. | Clare S. Functional MRI: Methods and Applications. PhD thesis: University of Nottingham 1997; 1-12. |
| 2. |
Hornak JP.
The Basics of NMR. Available from: |
| 3. | Lerner L, Horita DA. Teaching high-resolution nuclear magnetic resonance to graduate students in biophysics. Biophys J. 1993;65:2692-2697. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 3] [Cited by in RCA: 3] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 5. | Haacke ME, Brown RW, Thompson MR, Venkatesan R. Magnetic resonance imaging: Physical principles and sequence design. New York: John Wiley and Sons 1999; 3-13. |
| 7. | Brix G, Kolem H, Nitz WR, Bock M, Huppertz A, Zech CJ, Dietrich O. Basics of Magnetic Resonance Imaging and Magnetic Resonance Spectroscopy. Heidelberg: Springer Berlin 2008; 3-167. |
| 8. | Posadas AND, Tannus A, Panepucci CH, Crestana S. Magnetic Resonance Imaging as a non–invasive technique for investigating 3-D preferential flow occurring within stratified soil samples. Computers and Electronics in Agriculture. 1996;14:255-267. [DOI] [Full Text] |
| 10. | Chrysikopoulos HS. Clinical MR Imaging and Physics: A tutorial. Berlin: Springer Berlin Heidelberg 2009; 1-31. [DOI] [Full Text] |
| 11. | Shankar R. Principles of Quantum Mechanics. New York: Plenum Press 1994; 265-266. |
| 12. | Slichter CP. Principles of Magnetic Resonance. New York: Harper and Row 1963; 1-28. |
| 13. | Abragam A. The Principles of Nuclear Magnetism. Oxford: Clarendon Press 1961; 1-15. |
| 14. | Ernst RR, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in one and two Dimensions. Oxford: Oxford University 1990; 152-162. |
| 15. | Edison AS. Theory and Applications of NMR Spectroscopy. Online Lecture Notes: University of Florida, Florida, 2000: 5-6. Available from: http://nmrc.wsu.edu/files/ pdf/theory.pdf. . |
| 16. | Cowan BP. Nuclear Magnetic Resonance and Relaxation (First Edition). Cambridge: Cambridge University Press 1997; 1-6. |
| 17. | Lent AH, Hinshaw WS. An Introduction to NMR Imaging: From the Bloch Equation to the Imaging Equation. Proc of the IEEE. 1983;71:338-350. [DOI] [Full Text] |
| 18. |
Walker R. Mathematics of Nuclear Magnetic Resonance Imaging. Online Publications, 2011-03-08, cited 2013-09-01; 1-8 screens. Available from: |
| 19. | Wolff-Reichert B. A Conceptual Tour of Pulsed NMR. Online Lecture Notes: Department of Physics and Astronomy, University of Hawaii, Hawaii, 2008: 1-8. Available from: http://www.phys.hawaii.edu/~teb/phys481l/PS2A6_ConceptualTour.pdf 2008; . |
| 20. | Awojoyogbe OB, Dada M. Mathematical Design of a Magnetic Resonance Imaging Sequence based on Bloch NMR Flow Equations and Bessel Functions. Chinese Journal of Magn Reson Imaging. 2013;5:373-381. [DOI] [Full Text] |
| 21. |
NMR determined Rotational correlation time. University of Buffalo Online Publication, 2011-10-13, cited 2013-09-01. Available from: |
| 22. | Wang Y. Physics of MRI. Online Lecture Notes: Polytechnic University, Brooklyn, New York,2006: 15-25. Available from: http://eeweb.poly.edu/~yao/EL5823/MRI_physics_ch12.pdf; . |
| 23. | Peleg Y, Pnini R, Zaarur E. Schaum’s Outline of Theory and Problems of Quantum Mechanics. New York: McGraw-Hill Professional 1998; 123-124. |
| 24. | Dada OM, Awojoyogbe OB, Adesola OA, Boubaker K. Magnetic Resonance Imaging-derived Flow Parameters for the Analysis of Cardiovascular Diseases and Drug Development. Magnetic Resonance Insights. 2013;6:83-93. [RCA] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 1] [Cited by in RCA: 1] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 25. | Awojoyogbe OB. A quantum mechanical model of the Bloch NMR flow equations for electron dynamics in fluids at the molecular level. Phys Scr. 2007;75:788. [DOI] [Full Text] |
| 26. | Awojoyogbe OB, Dada OM, Faromika OP, Dada OE. Mathematical Concept of the Bloch Flow Equations for General Magnetic Resonance Imaging: A Review. Concep in Magn Reson Part A. 2011;38A:85-101. [DOI] [Full Text] |
| 27. | Bottomley PA, Foster TH, Argersinger RE, Pfeifer LM. A review of normal tissue hydrogen NMR relaxation times and relaxation mechanisms from 1-100 MHz: dependence on tissue type, NMR frequency, temperature, species, excision, and age. Med Phys. 1984;11:425-448. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 907] [Cited by in RCA: 842] [Article Influence: 20.5] [Reference Citation Analysis (0)] |
| 28. | Carneiro AAO, Vilela GR, de Araujo DB, Baffa O. MRI relaxometry: methods and applications. Braz J Phys. 2006;36:9-15. [DOI] [Full Text] |
| 29. | Quigley MF, Iskandar B, Quigley ME, Nicosia M, Haughton V. Cerebrospinal fluid flow in foramen magnum: temporal and spatial patterns at MR imaging in volunteers and in patients with Chiari I malformation. Radiology. 2004;232:229-236. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 102] [Cited by in RCA: 104] [Article Influence: 5.0] [Reference Citation Analysis (0)] |
| 30. | Compston A, Coles A. Multiple sclerosis. Lancet. 2002;359:1221-1231. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1514] [Cited by in RCA: 1471] [Article Influence: 64.0] [Reference Citation Analysis (0)] |
| 31. | Miller SP, Vigneron DB, Henry RG, Bohland MA, Ceppi-Cozzio C, Hoffman C, Newton N, Partridge JC, Ferriero DM, Barkovich AJ. Serial quantitative diffusion tensor MRI of the premature brain: development in newborns with and without injury. J Magn Reson Imaging. 2002;16:621-632. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 259] [Cited by in RCA: 247] [Article Influence: 10.7] [Reference Citation Analysis (0)] |