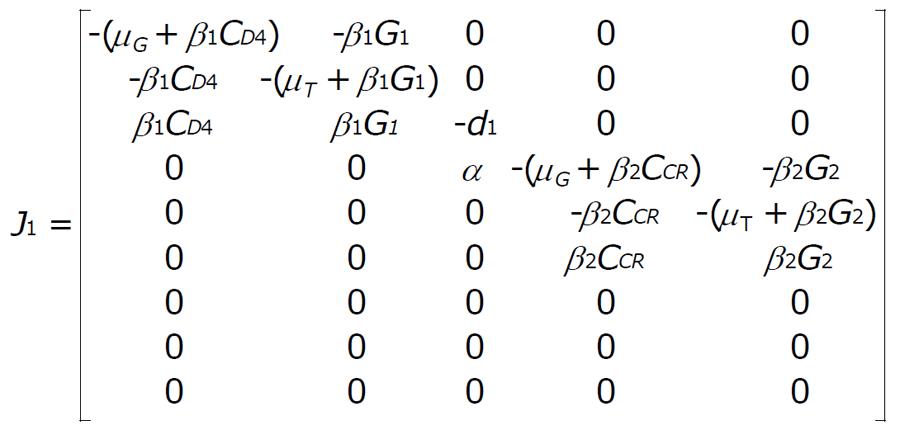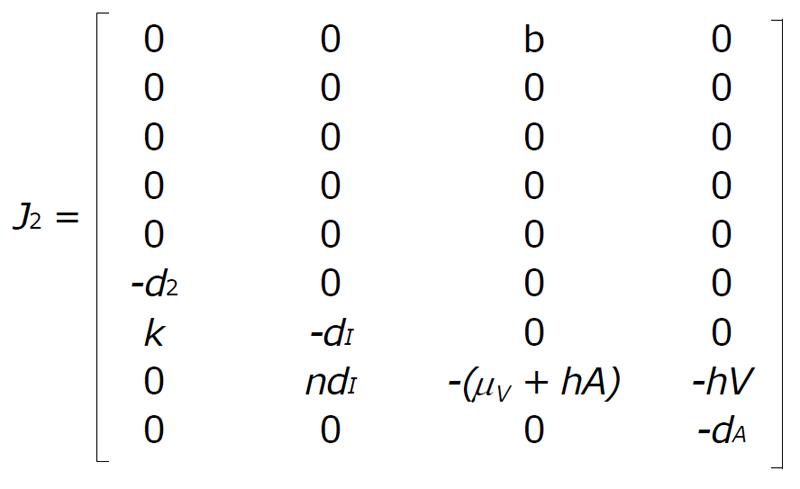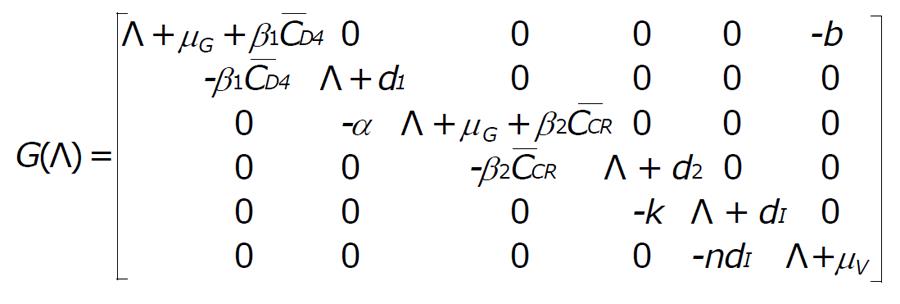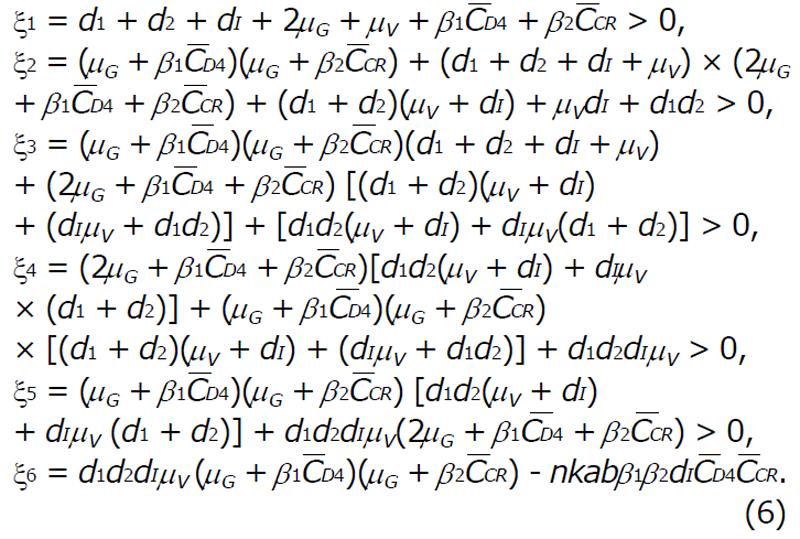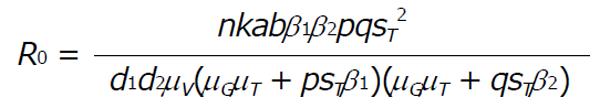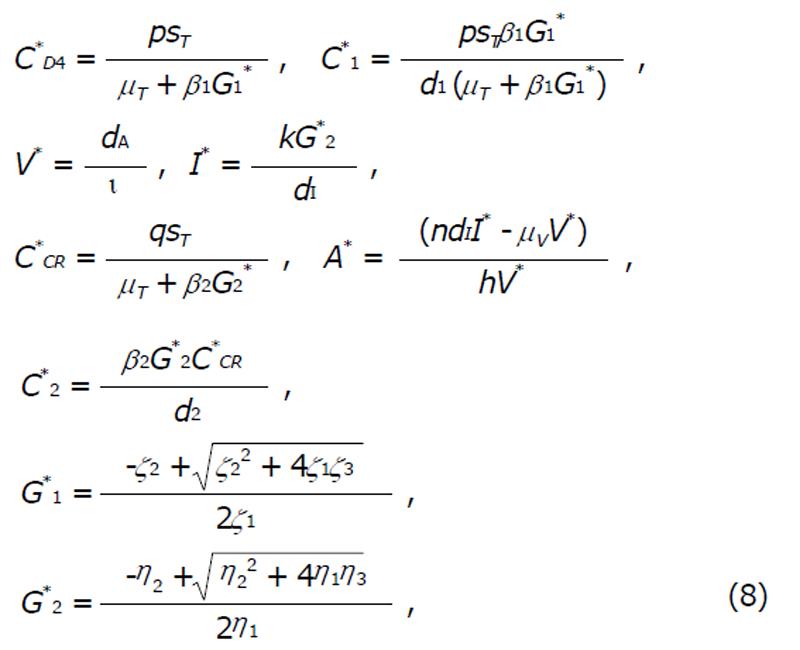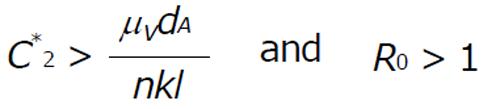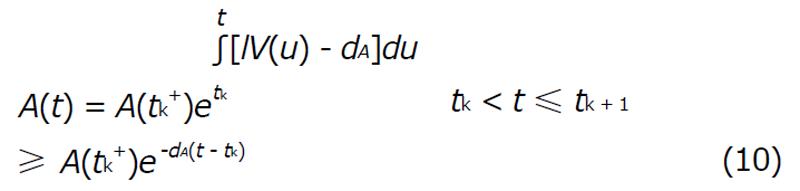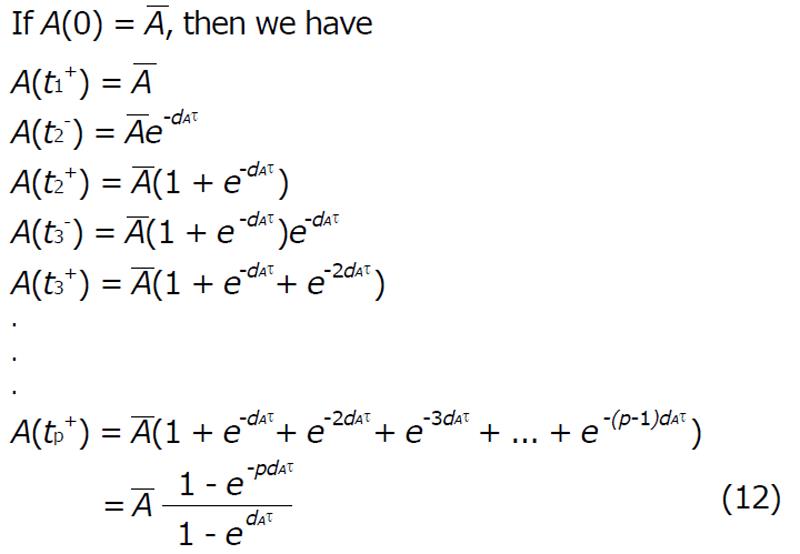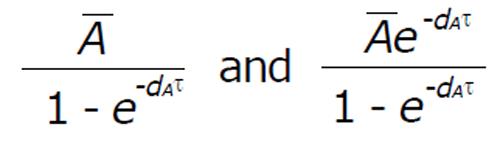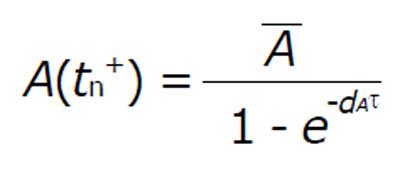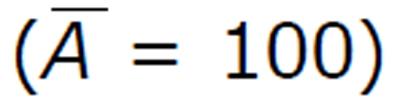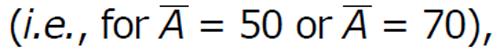Published online Nov 12, 2015. doi: 10.5501/wjv.v4.i4.356
Peer-review started: November 2, 2014
First decision: April 22, 2015
Revised: May 19, 2015
Accepted: June 1, 2015
Article in press: June 2, 2015
Published online: November 12, 2015
Processing time: 375 Days and 14.5 Hours
Entry of acquired immune deficiency syndrome virus into the host immune cell involves the participation of various components of host and viral cell unit. These components may be categorized as attachment of the viral surface envelope protein subunit, gp120, to the CD4+ receptor and chemokine coreceptors, CCR5 and CXCR4, present on T cell surface. The viral fusion protein, gp41, the second cleaved subunit of Env undergoes reconfiguration and the membrane fusion reaction itself. Since the CD4+ T cell population is actively involved; the ultimate outcome of human immunodeficiency virus infection is total collapse of the host immune system. Mathematical modeling of the stages in viral membrane protein-host cell receptor-coreceptor interaction and the effect of antibody vaccine on the viral entry into the susceptible host cell has been carried out using as impulsive differential equations. We have studied the effect of antibody vaccination and determined analytically the threshold value of drug dosage and dosing interval for optimum levels of infection. We have also investigated the effect of perfect adherence of drug dose on the immune cell count in extreme cases and observed that systematic drug dosage of the immune cells leads to longer and improved lives.
Core tip: Use of single-cell antibody-cloning techniques uncover naturally arising, broad and potent human immunodeficiency virus (HIV) neutralizing antibodies. These antibodies can protect against infection and suppress new HIV infection. This antibody vaccination gives new ideas about the fight against the HIV infection. From the analytical study of the effect of antibody vaccination we found the threshold value of drug dosage and dosing interval for optimum levels of infection. We have also investigated the effect of perfect adherence of drug dose on the immune cell count in extreme cases and observed that systematic drug dosage of the immune cells leads to longer and improved lives.
- Citation: Chatterjee AN, Saha S, Roy PK. Human immunodeficiency virus/acquired immune deficiency syndrome: Using drug from mathematical perceptive. World J Virology 2015; 4(4): 356-364
- URL: https://www.wjgnet.com/2220-3249/full/v4/i4/356.htm
- DOI: https://dx.doi.org/10.5501/wjv.v4.i4.356
Over the last two decades there has been extensive research on the area of human immunodeficiency virus (HIV) infection invading the human immune system. According to the World Health Organisation (WHO), almost 75 million people have already been infected with the HIV virus and about 36 million people have died of HIV. Globally, 35.3 million people were living with HIV at the end of 2012. An estimated 0.8% of adults aged 15-49 years worldwide are living with HIV, although the burden of the epidemic continues to vary considerably between countries and regions. Sub-Saharan Africa remains most severely affected, with nearly 1 in every 20 adults living with HIV and accounting for 71% of the people living with HIV worldwide. CD4+ T lymphocyte count is the only way to discover the disease progression monitoring during anti retroviral treatment (ART). From the premature days of infection, CD4+ T-lymphocyte cells have been acknowledged as most important for HIV disease progression[1]. A healthy human adult has about 1000 CD4+ T cells per microliter of blood[1], and when the number of CD4+ T cells is reduced below 200/μL, as HIV infected patient considered as acquired immune deficiency syndrome (AIDS) patients[2,3]. The infection process of the human cells by the human immunodeficiency virus (HIV) is very complicated process. When HIV invades into the body, it targets the immune cells, mainly the CD4+ T cells. HIV virus can easily hit into CD4+ T cells by a binding process between the envelope proteins (gp41/gp120) on the surface of HIV with both the CD4 receptor and the chemokine coreceptor. The entry process is initiated by binding of gp120, a cleaved subunit of viral surface envelope protein, Env, to the CD4+ receptor present on the T cell surface. However, this binding will be futile unless a conformational change is induced in gp120 resulting in exposure of a coreceptor binding site and enabling it to bind to as N-terminus of chemokine coreceptor, namely CCR5 and CXCR4, when a heterotrimeric complex of gp120 - CD4-coreceptor is formed. Basically, the chemokines are small soluble paracrine signaling molecules involved in trafficking and recruitment of leukocytes to sites of injury and inflammation. Chemokines and their receptors contribute significantly to disease progression in HIV-afflicted patients. Co-receptor availability and expression determine host susceptibility to infection. These coreceptors are determinants of viral tropism. After that, viral fusion occurs in the target cell membrane and the genetic material viral RNA gets entry into the CD4+ T cell. This genetic material has a reverse transcriptase enzyme. By the reverse transcription process the RNA genome is reverse-transcribed to a DNA copy, and thus the cell becomes infected. This provirus can enter into the host cell genome where it can stay in an actively infected state or a latently infected state.
Virus specific antibodies are created by a complex differentiation pathway that includes B cell proliferation, isotype switching, germinal center formation and affinity maturation[4]. As a result, the presence of specific antibody secreting plasma cells and antibody production tends to continue long after the infection. In this outlook we consider B cell responses by assuming that antibodies are produced in response to free virus and that antibody production diminishes at a certain rate. But the antibody response diminishes during the course of infection and thus the immune system cannot fight against the HIV.
A recent vaccine experiment shows the use of single-cell antibody-cloning techniques that uncovered naturally arising, broad and potent HIV neutralizing antibodies (bNAbs)[5]. It is observed experimentally that these antibodies can defend against infection and suppress HIV infection in animals. The invention of this antibody vaccination gives new ideas about the fight against the HIV infection. The most contemporary approach to study the drug dynamics is determined by use of impulsive differential equations. Perfect or imperfect drug adherence and drug holidays can make easy the development of resistance. In recent years the effects of perfect adherence to antiretroviral therapy have been studied by impulsive differential equations[4,6-10]. Using this method, the dosing period and threshold values of dosage can be obtained more precisely. Also the effect of maximal acceptable drug holidays can be found by using impulsive differential equations[4]. Impulsive differential equations result if drug effect as well as that of the metabolites are assumed to decay with time in an exponential manner during each cycle and are assumed to change instantaneously at dosing times, tj for different drug doses and can result in either implicit or explicit models[6-8].
This article is arranged in the following manner: In the first section, we formulate the basic mathematical model on the basis of antibody responses against the virus and applying impulsive differential equations, we show how antibody responses on the human immune system. Analytical and numerical studies have been performed in the next sections. Lastly, we discuss the implication of the results which were found in the earlier sections.
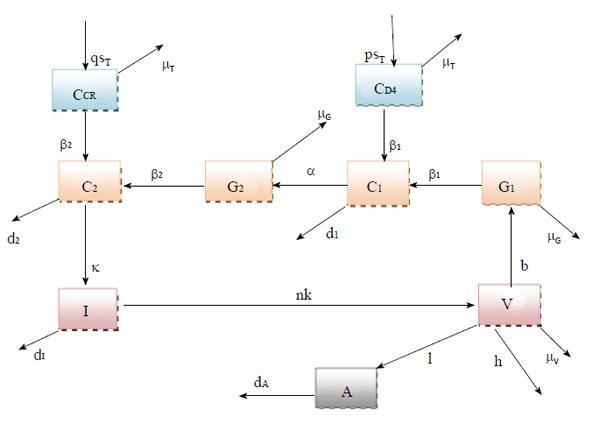
In this research article, we have modified the explicit mathematical model as proposed by Roy et al[11], considering the perfect adherence behavior of CTL vaccination in HIV infected patients. Here G1 represents the concentration of viral Env subunit, gp120 in vivo, and CD4 denotes the concentration of CD4 receptor on T cell surface. Let C1 be the concentration of the dimeric complex of gp120 and CD4 receptor, G2 be the concentration of viral fusion protein, gp41, and CCR be the concentration of the chemokine coreceptor on CD4+ cells. Also, C2 be the concentration of the combination of gp120 and gp120 - CD4 chemokine coreceptor ternary complex, I denote the concentration of infected CD4+ T cells, and V denote the concentration of HIV virus. The model is represented in Figure 1. Here A stands for concentration of antibody response. We suppose that antibody responds proportionally to the production of free virus particles at a rate IVA. Antibody responses neutralize free virus particles at a rate hVA. In presence of antibody vaccination through perfect adherence, the model is given by:
Math 1
In the system (1), b represents the multiplication capacity of gp120 in response to virus. The parameter a represents the successful exposure of gp41, since it is exposed only after attachment between gp120 and the CD4 receptor is complete. The parameter μ denotes the decay of gp120 and gp41, and β1 denotes the bonding force between gp120 and the CD4 receptor. Further β2 denotes the bonding force between the dimeric complex of gp120 and CD4 receptor and also the chemokine coreceptor. The source of susceptible CD4+ T cells is represented by sT, and p and q denote the number of CD4 receptors and chemokine coreceptors on one CD4+ T cell respectively. The death rate of healthy CD4+ T cell μT and the death rate of infected CD4+ T cells is dI. The dissociation rate of C1 and C2 are d1 and d2 respectively and for the sake of simplicity, it is assumed that after dissociation of C1 and C2, they will not return to their respective components. Here n represents the number of virus particles that are produced by one infected CD4+ T cell. The clearance rate of free HIV virus is represented as μV. Antibody responses by A are produced at a rate l and dA indicates the death rate of antibody responses. The concentration of antibodies (bNAbs) is represented by A(t) in plasma. The drug dose,
Math 2
that is taken at each impulse time tj (j = 1, 2, 3...) is kept constant. Since vaccination may be taken at either regular or irregular intervals, we have considered. The impulse time tj to be fixed. The system (1) together with the system (2) represent the dynamics with vaccine. The vaccination interval τ = tj + 1 - tj is fixed. Here we have only analyzed the models (1) - (2).
To study the model (1) together with (2), we first analyze the model in absence of drug. When drug is not administered to the system, we have observed that there exist two equilibrium point: (1) The disease free equilibrium point
Math 3
and (2) The endemic equilibrium point E*.
The disease free state: In absence of drug, there may exist disease free equilibrium point
Math 4
which is given by
Math 5
Now for the system (1) and (2) the Jacobian matrix is J = [J1|J2], where
Math 6
and
Math 7
The characteristic equation for the disease free equilibrium
Math 8
is
(Λ + dA)(Λ + μT)2G(Λ) = 0. (4)
where
Math 9
we get,
G(Λ) = Λ6 + ξ1Λ5 + ξ2Λ4 + ξ3Λ3 + ξ4Λ2 + ξ5Λ + ξ6 = 0, (5)
where,
Math 10
For ξ6 > 0 there exist no positive roots and all roots are negative. Hence, the basic reproduction R0 is,
Math 11
Remark: At disease free equilibrium point E, the system is locally stable if the basic reproduction number R0 < 1 and the system is unstable when R0 > 1.
The endemic state: There exists another equilibrium in the form of endemic equilibrium (E*),
(G*1, C*D4, C*1, C*2, C*CR, C*2, I*, V*, A*) (7)
where,
Math 12
and,
Math 13
The endemic state with antibody response exist if the concentration of the combination of gp41 and gpl20-CD4-chemokine coreceptor ternary complex (C2) satisfy the condition
Math 14
In this article, our main aim is to justify the effect of antibody vaccination mathematically. So we have not carried out the stability analysis for the endemic state. However we have derived the existence condition for the endemic state. Moreover we have carried out the numerical illustration for the endemic state and verified that the endemic state exist when R0 > 1.
To study the impulsive system it is assumed that the vaccine is taken at regular intervals with length τ = tk + 1 - tk. For a impulsive cycle tk≤t≤tk + 1, the solution is
Math 15
Suppose that A(tk-) denots the value immediately before the impulse and A(tk+) is the value immediately after. Calculating the least value of the concentration of A(t) for the perfect adherence with fixed interval length (τ > 0) we get
Math 16
This is the required concentration of antibody response to control the virus.
Math 17
Hence,
Math 18
The periodic end points of the trajectories are
Math 19
For perfect vaccination, the antibody response after the nth vaccination is
Math 20
For perfect adherence, to control the virus and avoid resistance, the minimum value (A*) of the periodic orbit must satisfy:
Math 21
Which implies that
Math 22
Remark: If we can restrict the dosing interval of τ satisfying the condition 0 ≤τ < τmax (for fixed vaccination) then the disease can be controlled. However, if τ > τmax, the disease progression continues, even if drug is administered at fixed intervals. Thus maintenance of optimum dosage regimen is essential in order to control the disease effectively.
In our numerical illustration, we have described the perfect drug adherence of antibody vaccination. All the parameters are taken from Table 1. We have assumed the initial condition as G1(0) = 2100, CD4(0) = 800, C1(0) = 0, G2(0) = 1050, CCR(0) = 800, C2(0) = 0, I(0) = 0, V(0) = 50, A(0) = 100 and the unit of the concentration is mm-3.
| Parameter | Value (units) | Ref. |
| b | 42 (per day) | [6] |
| β1 | 10-5 (/mm3/d) | [6] |
| μG | 5 (per day) | [9] |
| p | 1 (per day) | [6] |
| ST | 80 (/mm3/d) | [9] |
| μT | 0.05 (per day) | [6] |
| d1 | 0.4 (per day) | [6] |
| α | 25 (per day) | [6] |
| β2 | 10-5 (/mm3/d) | [6] |
| q | 0.6 (per day) | [6] |
| d2 | 0.4 (per day) | [6] |
| κ | 0.6 (per day) | [6] |
| dI | 0.5 (per day) | [9] |
| δ | 0.01 (per day) | [7] |
| n | 540 | [6] |
| μV | 3 (per day) | [7] |
| ι | 0.01 (per day) | [12] |
| dA | 0.5 (per day) | [7] |
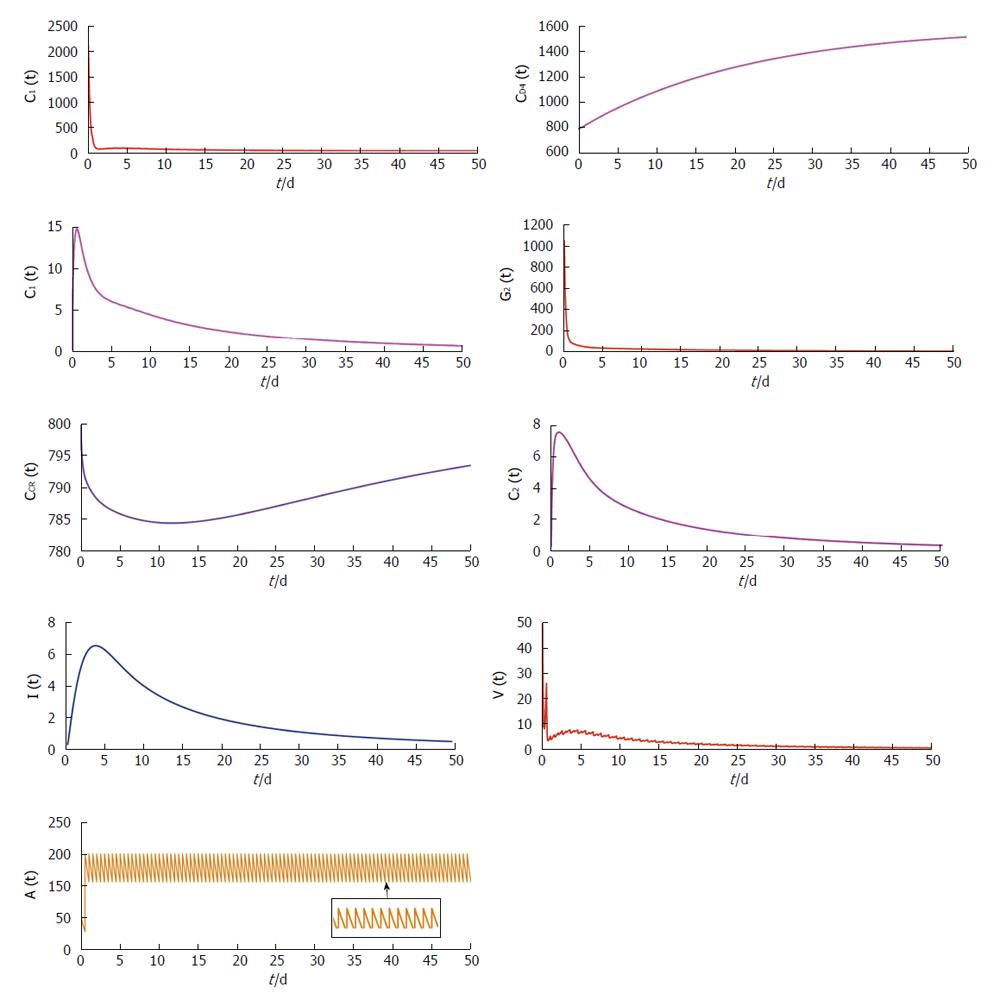
In Figure 2 we observe that in the presence of vaccination
Math 23
with frequent dosing interval (i.e., τ = 0.5), the virus population and infected CD4+ T cells population reduces. From this illustration, it can be predicted that proper antibody vaccination can restrict the infection process in HIV transmission. Now if the dosage of vaccination is not sufficient, then the effect of vaccination cannot be observed on the virus population and infected cell population.
In Figure 3, it is clearly observed that in presence of low vaccination
Math 24
the disease transmission process persists. Only adequate increment of the dosage of vaccination can restrict the disease progression. From these two figures we can predict that sufficient dosage of vaccination with frequent dosing interval can restrict the disease progression.
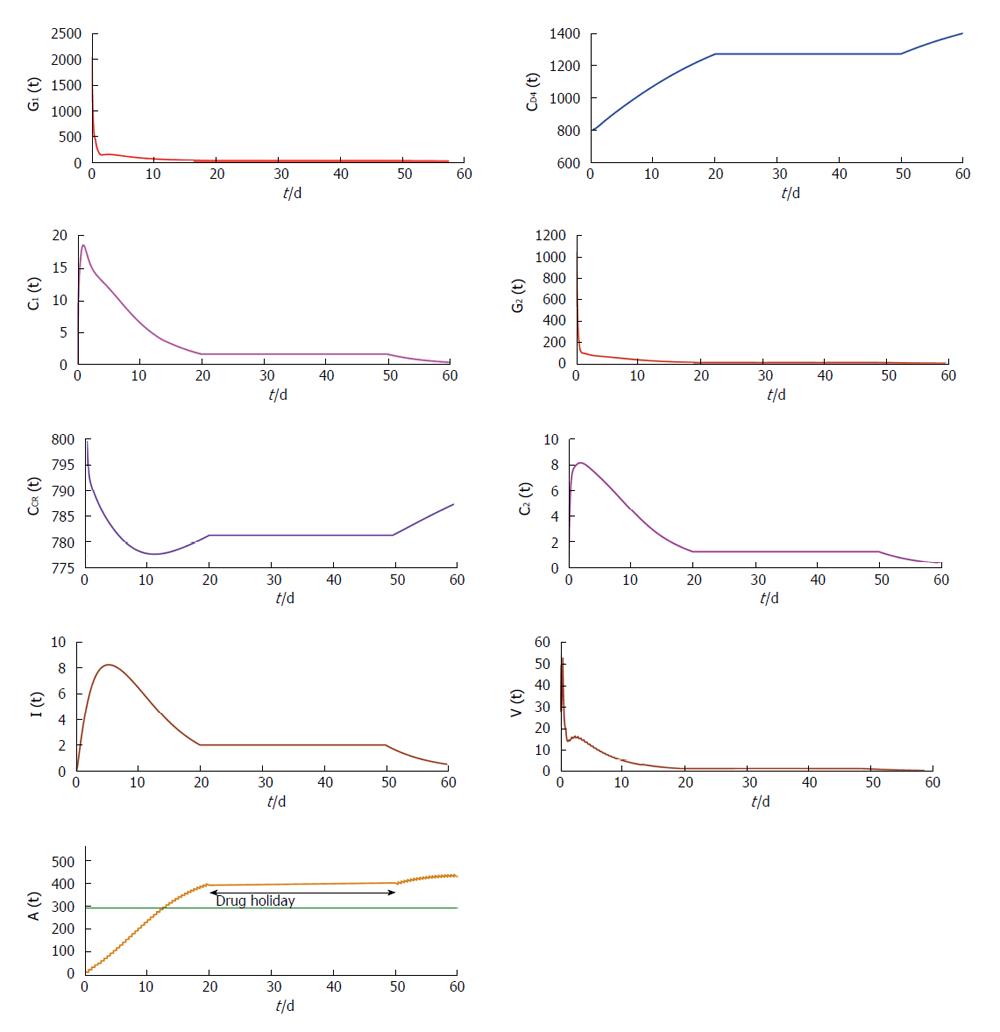
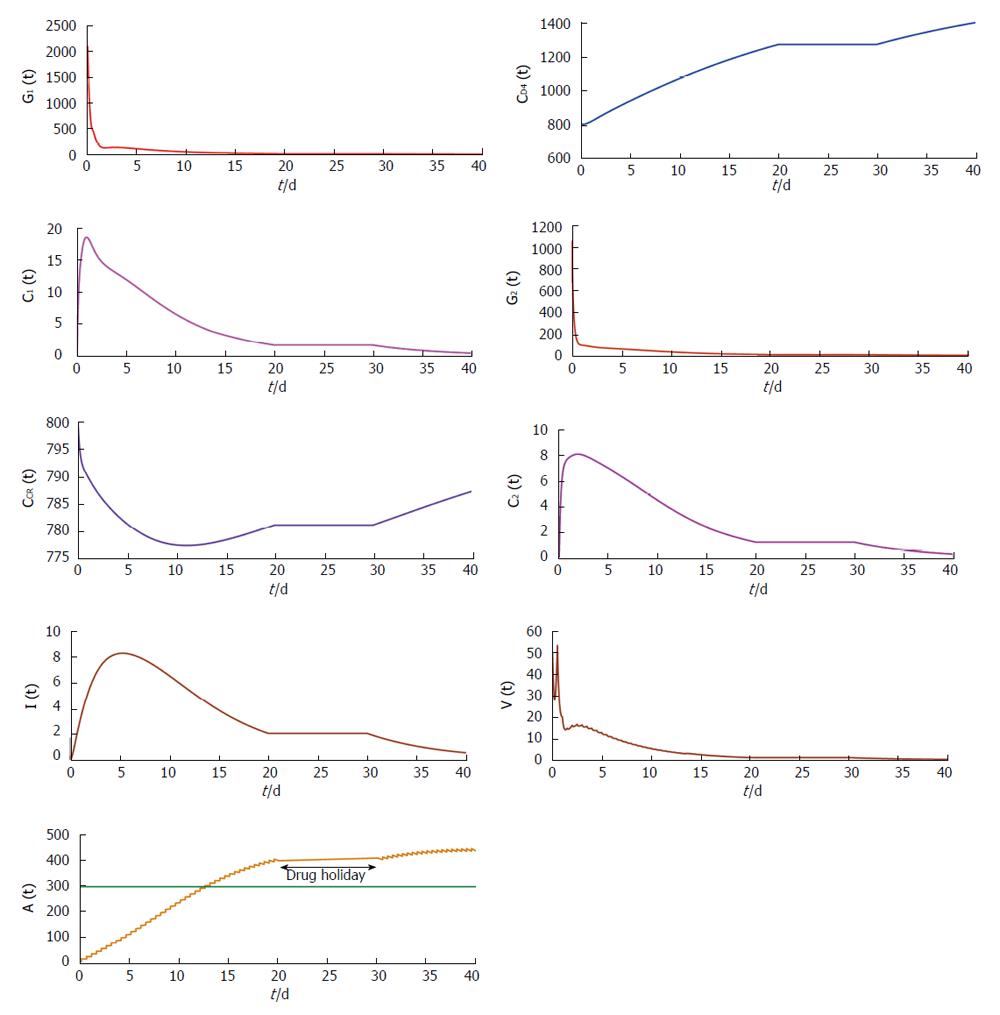
From Figures 4 and 5 we try to find out the effect of drug holidays. In Figure 4, we restrict the drug holidays 30 d, where as in Figure 5 the drug holidays is 10 d only. It is observed that when the drug holiday is 30 d the virus population attains its minimum value after 55 d. But if we restrict the drug holidays 10 d, the virus population attains its minimum value after 35 d. We also observe that for a 10 d drug holiday the CD4 receptor and CCR receptor attains its maximum concentration within 40 d. Whereas CD receptor and CCR receptor attains its maximum concentration within 60 d for 30 d drug holidays. Thus most unpleasant circumstances occur in case of long-term effects of the drug holidays.
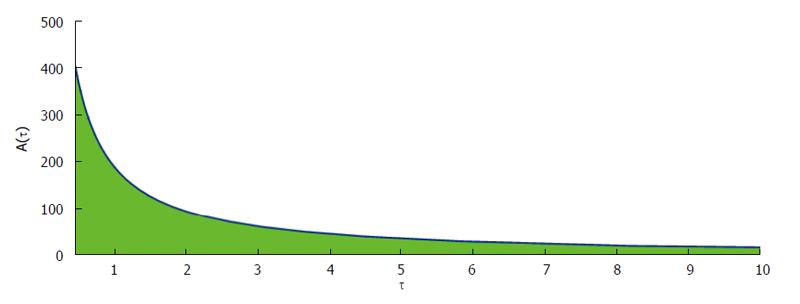
Figure 6 show that phase plane plotted against dosing interval and antibody responses. From this figure it is clearly observed that the antibody responses attain its maximum value if the drug dosing interval is frequent. Also the antibody responses reduce for the outsized dosing interval.
Antibody vaccination in AIDS therapy has been studied as a new policy. Here vaccination is delivered to the host system in an impulsive mode to reactivate the antibody response. Dosage of vaccination and dosing interval has been effectively studied by this present mathematical model. It has been observed that when basic reproduction ratio lies below one, we expect the system attain its disease free state. However, at R0 > 1, the system switches to endemic equilibrium. These conjectures have been supported by the results of numerical simulations.
It has been observed that the length of the dosing interval and the drug dose play a very decisive role in maintaining stable disease free equilibrium. From analytical as well as numerical finding it has been observed that the antibody responses attain its maximum value if the drug dosing interval is frequent. But the antibody responses reduce for the large dosing interval. Also we have observed that the drug holiday plays a pivotal role during the treatment schedule. From numerical findings we can predict that extensive drug holidays is unsafe for the treatment. Analytically and numerically, it has been observed that viral entry into the host cell is also inhibited with uninfected host CD4+ T cell population remaining unaffected. This happens because the antibody vaccination when administered following the best possible antibody responses can act against the free virus to neutralize free virus particles. This particular situation keeps the infected cell population at a very low level.
P- Reviewer: De Paschale M, Ghiringhelli PD, Krishnan T S- Editor: Ji FF L- Editor: A E- Editor: Yan JL
| 1. | Nowak M, May RM. AIDS pathogenesis: mathematical models of HIV and SIV infections. AIDS. 1993;7 Suppl 1:S3-18. [PubMed] |
| 2. | Perelson AS, Kirschner DE, De Boer R. Dynamics of HIV infection of CD4+ T cells. Math Biosci. 1993;114:81-125. [PubMed] |
| 3. | Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582-1586. [PubMed] |
| 4. | Miron RE, Smith RJ. Modelling imperfect adherence to HIV induction therapy. BMC Infect Dis. 2010;10:6. [PubMed] |
| 5. | Klein F, Mouquet H, Dosenovic P, Scheid JF, Scharf L, Nussenzweig MC. Antibodies in HIV-1 vaccine development and therapy. Science. 2013;341:1199-1204. [PubMed] |
| 6. | Lou J, Smith RJ. Modelling the effects of adherence to the HIV fusion inhibitor enfuvirtide. J Theor Biol. 2011;268:1-13. [PubMed] |
| 7. | Smith RJ, Aggarwala BD. Can the viral reservoir of latently infected CD4(+) T cells be eradicated with antiretroviral HIV drugs? J Math Biol. 2009;59:697-715. [PubMed] |
| 8. | Smith RJ. Explicitly accounting for antiretroviral drug uptake in theoretical HIV models predicts long-term failure of protease-only therapy. J Theor Biol. 2008;251:227-237. [PubMed] |
| 9. | Smith RJ, Wahl LM. Drug resistance in an immunological model of HIV-1 infection with impulsive drug effects. Bull Math Biol. 2005;67:783-813. [PubMed] |
| 10. | Lou J, Chen L, Ruggeri T. An Impulsive Differential Model on Post Exposure Prophylaxis to HIV-1 Exposed Individual. J Biol Syst. 2009;17:659-683. [RCA] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 12] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 11. | Roy PK, Chatterjee AN, Majee SB. Effect of Chemokine Analog through Perfect Adherence in HIV Treatment: A Model Based Study. IJAMA. 2012;4:121-145. |
| 12. | Wodarz D, May RM, Nowak MA. The role of antigen-independent persistence of memory cytotoxic T lymphocytes. Int Immunol. 2000;12:467-477. [PubMed] |