INTRODUCTION
“In One Dimension, did not a moving Point produce a Line with two terminal points? In Two Dimensions, did not a moving Line produce a Square with four terminal points? In Three Dimensions, did not a moving Square produce-did not this eye of mine behold it-that blessed Being, a Cube, with eight terminal points? And in Four Dimensions shall not a moving Cube-alas, for Analogy, and alas for the Progress of Truth, if it be not so-shall not, I say, the motion of a divine Cube result in a still more divine Organization with sixteen terminal points? Behold the infallible confirmation of the Series, 2, 4, 8, and 16 is not this a Geometrical Progression? Is not this-if I might quote my Lord’s own words-strictly according to Analogy?” From Flatland: A romance of many dimensions, Edwin A. Abbott.
The complexity of nature, characterized by its various degrees of irregularity and diverse physical properties[1], is a challenging topic. The Scottish biologist and mathematician D’Arcy Wentworth Thompson (1860-1948) proposed that the form of an anatomical entity can be identified through its dimensions and contour. However, Euclidean-based morphometric analyses, which involve measurements like area, perimeter, and form factor, fall short in accurately describing natural, including anatomical, entities due to their irregular shapes that cannot be quantified by means of the classical Euclidean geometry, which is only able to describe regular geometrical objects. Mandelbrot[2] (1924-2010) introduced the notion of fractal geometry[3] and coined the term “fractal” to describe spatial or temporal irregular patterns[4,5]. Fractal geometry has been suggested as an instrument to define the geometry of various natural entities, such as mountains, coastlines, clouds, trees, molecular structures, and an array of forms within anatomical systems along with their underlying dynamic processes[6]. The gastrointestinal or digestive system is a complex network of organs including the mouth, pharynx, esophagus, stomach, small and large intestines, rectum, and anus, as well as the salivary glands, liver, gallbladder, and pancreas. The morphological intricacy of the gastrointestinal system, both in its natural state and under pathological conditions, is mainly characterized by its irregularity and self-similarity across varying scales[7]. Classical examples of irregularly-shaped histological entities that defy Euclidean geometric principles include gastric pits, which are indentations in the stomach signifying entrances to tubular gastric glands, and villi, which are finger-like structures that significantly increase the surface area of the small intestine[8]. The human stomach is known to have millions of these pits across the surface of its lining epithelium. The adult small intestine, with an average inner surface area of around 30 m2[9,10], necessitates such a large surface for effective metabolism and nutrient absorption. This is achieved by forming unique irregularly-shaped structures like villi and microvilli. The functional efficiency of epithelia is enhanced by their fractal organization, which expands the surface area for processes like absorption or sensory reception, thereby enabling more efficient interaction with the external environment[11]. This level of surface area and functional efficiency would be unattainable if the colonic mucosa were to be represented by a two-dimensional Euclidean plane. However, the fractal-like characteristics observed in epithelial tissues, which line organ surfaces and body structures, are not universal but rather specific to certain instances. The liver development, commonly described as a fractal-like phenomenon, involves intricate processes and interactions among various cell types. During embryonic development, a bud-like structure known as the hepatic diverticulum, which emerges from the endodermal layer of the early gut tube, forms the liver. The hepatic diverticulum then undergoes branching morphogenesis, leading to a complex network of interconnected structures that enable liver tissue expansion and development of bile ducts, blood vessels, and functional units like lobes or lobules. Similarly, pancreas development is a regulated process involving growth and branching. While the developing liver and pancreas’ branching patterns may superficially resemble fractal structures, it’s crucial to acknowledge that true fractals display self-similarity across multiple scales, a trait not precisely seen in liver development. Fractal geometry has been used to describe pathological entities within the gastrointestinal system as well. The irregularity in the shape of the interface between epithelial and connective tissues is a recognized characteristic of malignant and pre-malignant epithelial lesions. However, efforts to objectively assess this have been sparse. Landini and Rippin[12] have applied fractal geometry as an instrument for evaluating this irregular epithelial-connective tissue interface[13]. Intestinal polyps, characterized by abnormal tissue overgrowth within the intestinal lining, can display varying shapes and structures based on factors like the type of polyp (i.e., adenomatous polyps, hyperplastic polyps), their location, and size. Some polyps, such as villous adenomas, appear to exhibit a self-similar form, hinting at a possible fractal structure within a specific magnification range. The fractal dimension has been leveraged to quantify these polyps, proving to be a more effective discriminator between diagnostic groups than Euclidean measures like area or perimeter length[14]. Several studies suggest that fractal estimation could offer a novel method for examining the nonlinear dynamics of the gastrointestinal system. This approach sheds light on the complexity and unevenness of colonic pressure activity during different periods, providing potential applications for understanding gastrointestinal system functions. As fractal analysis becomes increasingly prevalent in biomedical research, it serves to quantify the irregularities of anatomical entities, their generation patterns, and their physiological and pathological processes. In this context, we delve into the potential of fractal geometry as a tool for understanding the gastrointestinal system and its possible applications in clinical practice.
FRACTAL GEOMETRY: BASIC PRINCIPLES
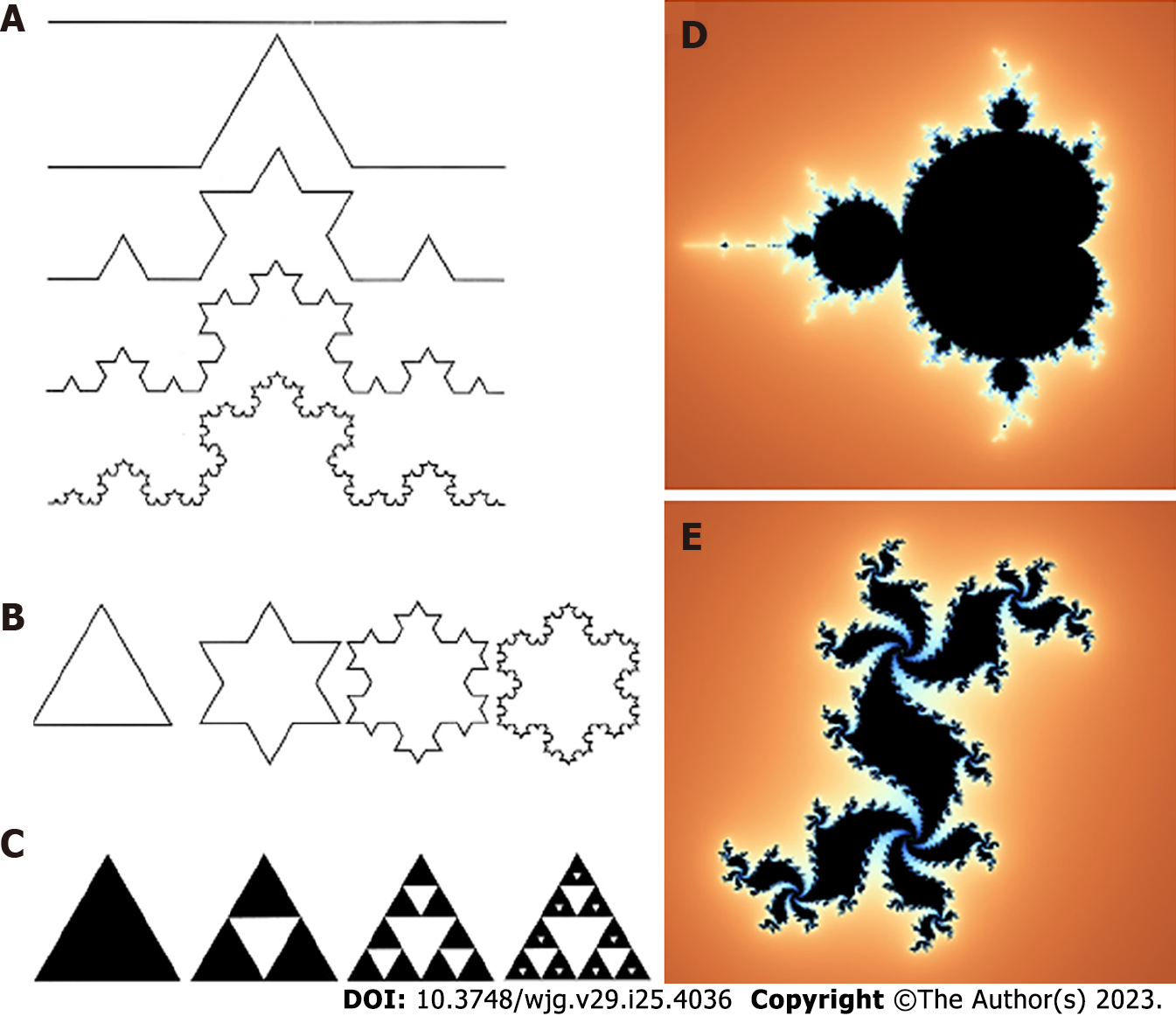
Fractals, whether anatomical or natural, are characterized by four primary attributes: (1) Irregularity in shape; (2) self-similarity in structure; (3) non-integer or fractal dimension; and (4) scaling. Scaling indicates that the measured features of a fractal depend on the scale at which they are observed[15]. The most significant characteristic of fractal objects is their ability to display similar patterns at different scales, resulting in the component parts having a form that is similar to the whole in all dimensions. Complex curves such as coastline shapes serve as typical examples of this property, where each segment can be regarded as a smaller version of the complete structure in a statistical sense (Figure 1). The term “self-similarity” refers to a property of fractals that can be either geometric or statistical. Geometric self-similarity occurs when every smaller piece of an object is an exact replica of the whole object. For instance, the “snowflake” and the “curve”, both described by Swedish mathematician Niels Fabian Helge von Koch (1870-1924) in 1904, are examples of geometrically self-similar figures[16]. Another geometrically self-similar figure is the “Sierpinski triangle”, originally described by Polish mathematician Waclaw Sierpinski (1882-1969) in 1915. In contrast, statistical self-similarity pertains to biological objects, including natural objects (Figure 2) and anatomical forms (Figure 3). While small components of anatomical systems are not typically exact replicas of the entire system, they still exhibit self-similarity. For instance, if we examine a segment of a tree branch or vascular vessel, it may not look identical to the entire tree or vessel, but it still displays self-similarity. Many anatomical structures have been identified as statistical self-similar entities, including the circulatory system, the biliary tree of the liver, the dendritic structure of neuronal cells, the ductal system of glands, the cell membrane, and the extra-cellular matrix (ECM) in cases of chronic liver disease[17].
Figure 1 Examples of geometrical self-similar objects.
A: “Curve” from Niels Fabian Helge von Koch; B: “Snowflake” from Niels Fabian Helge von Koch; C: “Sierpinski triangle”; D: Mandelbrot set; E: Julia set named after the studies on the geometrical complexity by the French mathematicians Gaston Julia e Pierre Fatou.
Figure 2 Examples of natural statistical self-similar structures resembling mathematical fractals.
A: Marine invertebrates corals; B: Tree branches; C: Water breaking waves; D: Sand dunes.
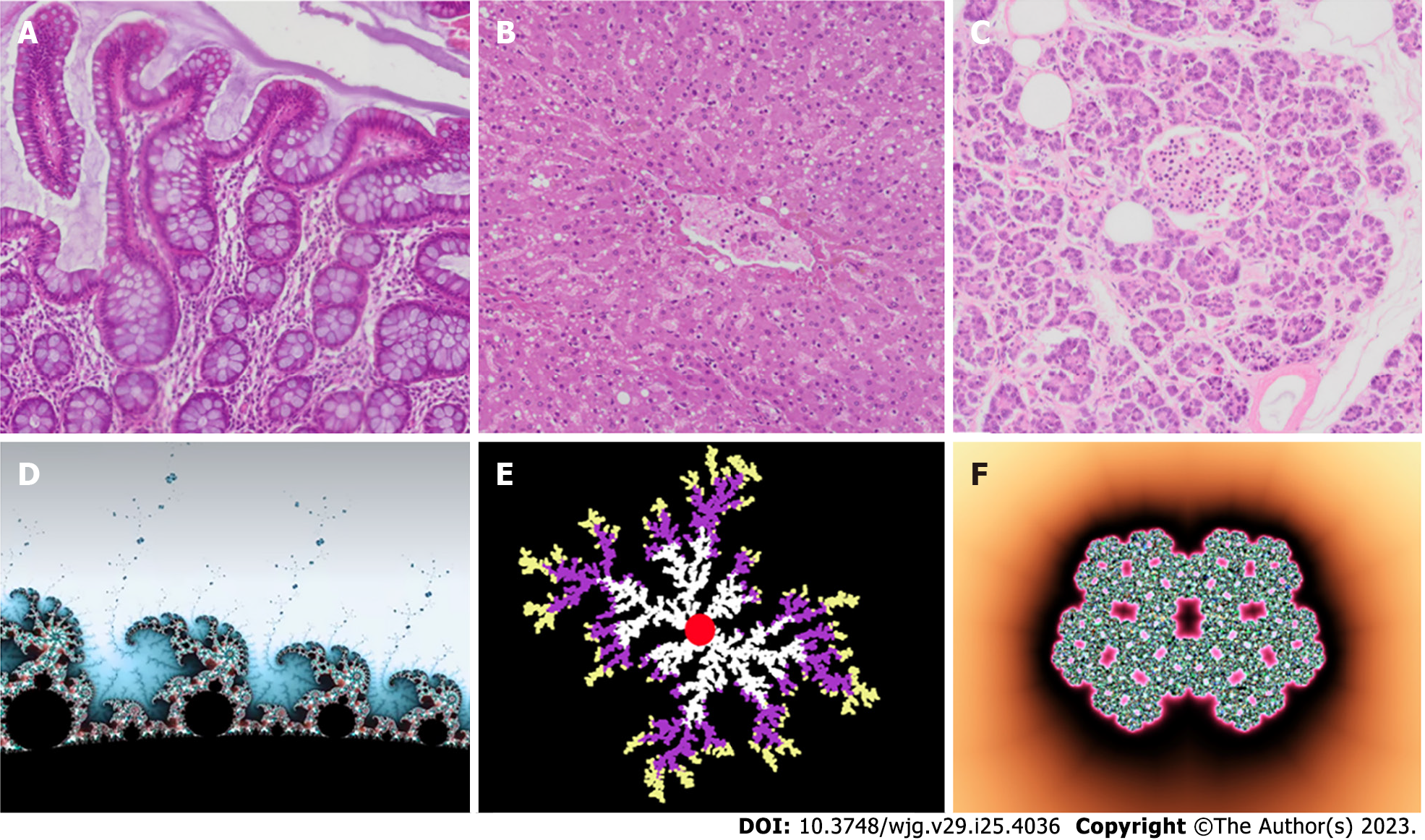
Figure 3 Some self-similar tissues in the gastrointestinal system and their corresponding idealized mathematical fractals.
A: Intestine villi; B: Liver; C: Pancreatic Langerhans islet; D: Mandelbrot set; E: Diffusion-limited aggregation model; F: Julia fractal islet.
The concept of “dimension” is a fundamental aspect of fractals and represents a characteristic value of the object. There are two definitions of dimension: the first is the “topological dimension”, introduced by Austrian mathematician Karl Menger (1902-1985), which assigns an integer number to each point in three-dimensional Euclidean space (E3). For example, a “point” is assigned a dimension of 0, a “straight line” a dimension of 1, a “plane surface”a dimension of 2, and a “three-dimensional figure” a dimension of 3. The second definition was introduced by Felix Hausdorff (1868-1942) and Abram Besicovitch (1891-1970), who assigned a “real number” between the topological dimension and 3 to every natural object in E3. Mandelbrot designated Menger’s dimension with the symbol Dγ and Hausdorff and Besicovitch’s dimension with the symbol D. For all Euclidean figures, Dγ and D are equivalent (Dγ = D). However, this equality does not apply to all fractal natural objects, as the inequality D > Dγ is true. Many methods have been proposed to estimate the fractal dimension, with the “box-counting method” being the most widely used in biomedical sciences to estimate the space-filling properties of anatomical objects in two-dimensional and three-dimensional space.
It applies the following formula: D = lim ε→0 [logN(ε)/Log(1/ε)], where D is the box-counting fractal dimension of the object, ε is the side length of the box, and N(ε) is the smallest number of boxes of side ε required to cover the outline or the surface of the object completely. Because the zero limit cannot be applied to natural objects, the dimension was estimated by the formula D = d, where d is the slope of the graph of Log N(ε) against Log (1/ε). The linear segments of these graphs were identified using the least-squares method of regression, and the gradients of these segments are assessed using an iterative resistant-line method[15,18-25].
THE FRACTAL NATURE OF THE GASTROINTESTINAL SYSTEM
The fractal esophagus
Wax et al[26] conducted a quantitative analysis of nuclear morphometry in epithelial cells using an animal model of esophageal carcinogenesis in 2003. They observed changes in the size and texture of cell nuclei caused by neoplastic transformation and chemopreventive action[26]. However, the fractal dimension did not enhance the diagnostic ability of the technique for classifying neoplasia[26]. Instead, the increase in fractal dimension observed in dysplastic tissues corresponded with changes in the texture of cell nuclei observed in histological images, where clumped and grainy cell nuclei are typical of dysplasia. The authors concluded that the increased fractal dimension resulted from alterations in the organization of chromatin and proteins within the nucleus, as demonstrated by the changes in the visual appearance of cell nuclei in histological images[26]. A framework for creating a two-dimensional, globally interconnected map to simulate epithelium dynamics has been proposed by Hosseini and Hashemi Golpayegani[27]. The aim of this model was to facilitate early-stage dysplasia detection using microscopic imagery from endoscopic biopsies. Their findings suggested a potential direct correlation between the system’s structural complexity and the unpredictability of its dynamics[27]. Textural analysis of positron emission tomography (PET) and other imaging techniques is gaining interest in measuring intra-tumoral heterogeneity.
Studies have demonstrated that measuring tumor heterogeneity through textural analysis in 18F-fluorodeoxy glucose PET can provide predictive and prognostic information. In a study by Doumou et al[28], sixty-four patients with adenocarcinoma of the lower esophagus underwent 18F-FDG PET/CT imaging for clinical staging before surgery. Using in-house software implemented under MATLAB (The MathWorks Inc.) and calculating 57 textural features, including fractal indexes, they discovered that altering the “bin width” produced poor agreement for most second- and high-order features, with less impact on fractal parameters. The authors concluded that fractal analysis features were relatively resistant to changes in smoothing, segmentation, and bin width. In 2005, Gardner et al[29] noted that in normal subjects, patients with gastroesophageal reflux disease (GERD), and individuals with GERD treated with a proton pump inhibitor, both esophageal and gastric pH reflect an underlying stochastic process that generates a fractal pattern over time. The authors hypothesized that the fractal pattern of esophageal pH and gastric pH, along with the statistical association of sequential pH values for up to 2 h, encodes information regarding gastric acidity. They proposed that depending on the value of gastric acidity, gastroesophageal reflux causes the esophagus to signal the stomach to alter gastric acidity by influencing gastric secretion of acid or bicarbonate[29]. The authors subsequently confirmed their hypothesis by investigating 26 healthy adults with no history of gastrointestinal disease or symptoms and 27 adult subjects with a history of GERD who experienced heartburn at least four times per week for at least 6 mo[30] Their findings suggest that the esophagus can signal the stomach to alter gastric acidity, depending on the value of gastric pH, and that this ability is impaired in subjects with GERD. Thus, the self-similar, fractal pattern encodes information about gastric acidity that the esophagus can decode and, when necessary, signal the stomach to reduce gastric pH.
The fractal stomach
In 1994, Demling and Ell[31] conducted a study titled “Fractal stomach ulcer. A new measurement parameter for benign and malignant changes for the future”, proposing that fractal geometry could be beneficially applied for the spatial and temporal analysis of the stomach. Abdominal sound analysis is known to aid in the diagnosis of gastrointestinal diseases, and bowel sounds originating from the stomach and intestine are highly variable over time. They are described as loose successions or clusters of sudden bursts. Realistic recordings of abdominal sounds are contaminated with noise and artifacts that must be differentiated from the bowel sounds. More recently, Kölle et al[32] suggested a method of intrinsic mode function-fractal dimension filtering based on a multivariate empirical mode decomposition approach. The intrinsic mode function-fractal dimension filtering method has been applied to a realistic, contaminated dataset, with close to 100% of manually labeled bowel sounds correctly identified[32]. In a novel approach, West et al[33] analyzed fluctuations in human myoelectric gastric activity noninvasively measured from the surface of the abdomen. They estimated the “scaling index” in 17 healthy individuals and found it to be statistically different from a set of surrogate data. The authors also demonstrated that the dynamical pattern of the gastric rate variability time series was significantly reduced in systemic sclerosis patients compared to healthy individuals, indicating a decrease in complexity of the underlying gastrointestinal control system. In terms of clinical relevance, employing fractal image analysis to model the conduction patterns of slow waves (SWs) through detailed networks of interstitial cells of Cajal can enhance our comprehension of the principles driving gastrointestinal myoelectric activity, as well as the diseases linked to its malfunction[34]. Interstitial cells of cajal (ICC) are specialized pacemaker cells in the gastrointestinal system responsible for generating and propagating SWs of depolarization throughout the muscularis propria. These SWs regulate the motility of the gastrointestinal system tract, which is essential for digestion, nutrient absorption, and waste elimination. By using a combined approach based on image analysis and fractal geometry of detailed ICC networks, researchers have demonstrated that modeling SW conduction patterns can aid in improving our understanding of the mechanisms underlying gastrointestinal system myoelectric activity and the diseases associated with its dysfunction[35,36].
Watanabe et al[37] applied fractal analysis to contrast-enhanced computed tomography (CT) images to estimate structural abnormality in gastric tumors and evaluated its biomarker value for predicting survival in surgically treated gastric cancer patients. The authors found that high fractal dimension values of tumors were significantly associated with high T stage and high pathological stage. Moreover, in Kaplan-Meier analysis, patients with higher fractal dimension tumors had significantly worse disease-specific survival, indicating that contrast-enhanced CT fractal analysis could be a useful biomarker for gastric cancer patients, reflecting clinic-pathologic features and survival.
In a study by Liliac et al[38], the pattern of E-cadherin at the cell membrane level was analyzed using fractal dimension analysis on fluorescence immunohistochemistry samples labeled with E-cadherin in gastric well/moderate and solid gastric adenocarcinoma from patients without any associated chemotherapeutic treatment or radiotherapy. The images were binarized using a fixed threshold of the E-cadherin fluorescence channel, and the fractal dimension of the binarized image outlines was calculated to assess the ruggedness of the cellular membranes. The study demonstrated that the morphological analysis of a simple marker for the cell membrane can identify and distinguish tumor cells.
The fractal colon
Cross et al[14] suggested that colorectal polyps have a self-similar structure that may contain fractal elements, and that the fractal dimension could be a useful morphometric discriminator. The authors estimated the fractal dimensions of images from hematoxylin and eosin-stained sections of 359 colorectal polyps, including 214 tubulovillous adenomas, 41 tubular adenomas, 29 villous adenomas, 68 metaplastic polyps, and 7 inflammatory polyps, and found that colorectal polyps exhibit a fractal structure within a defined range of magnification[14]. They concluded that fractal dimension can provide a new method of estimating polyp shape and serve as a useful morphometric discriminator between diagnostic categories[14].
It is clear that the invasive front of colorectal cancers (CRCs) can vary in complexity, ranging from smooth to highly complex when the front breaks up into small cell clusters or single cancer cells[39]. Currently, the degree of complexity is estimated visually and/or semi-quantitatively. Franzén et al[39] compared the visual estimation of CRC invasive front irregularity to different quantitative image analytical techniques and developed a “complexity index” for the invasive margin. They analyzed cytokeratin 8-stained tissue sections from 29 CRCs and found that the fractal dimension and tumor cell clusters provided the best correlation to visual grading using discriminant analysis. Moreover, the fractal dimension separated tumors up to a certain level of complexity, while tumor cell cluster counting distinguished cells above and beyond the fractal dimension when the tumor front fragmented into small cell clusters. These results suggest that the fractal dimension could be a valid index for objectively quantifying the complexity of tumor invasive fronts. In another study, Hahn-Strömberg et al[40] correlated the complexity of colon carcinoma invasive fronts with cell adhesion protein expression and polymorphisms in their genes. They constructed a “complexity index” using computer-assisted morphometry to estimate fractal dimension and tumor cell clusters, followed by tree analysis, for 32 colon carcinomas. Hahn-Strömberg et al[40] found that adhesion protein distribution was significantly altered in most carcinomas, but no correlation was observed between the complexity of the invasive border and protein distribution or genetic alterations. These findings indicate that the complexity of CRC invasion is not solely dependent on genetic derangements in adhesion protein genes or protein distribution, but also on aberrations in the function of other proteins related to adhesive proteins.
In their research, Ştefănescu et al[41] utilized fractal analysis and neural network modeling of colon mucosa images generated by confocal laser endomicroscopy to develop an automatic diagnosis algorithm for CRCs. They examined 1035 images of normal mucosa and tumor regions, processed using a computer-aided imaging system to achieve an automatic diagnosis. The researchers found that non-malignant colon mucosa has polyhedral crypt structures while malignant colon mucosa has irregular and interrupted crypts. They estimated seven parameters for each image, with only contrast, homogeneity and feature number showing significant differences between natural and cancer images. Their findings suggest that computed aided diagnosis through fractal analysis of glandular structures can be used in combination with traditional histological and minimally invasive imaging methods[41]. Another study by Shaleve et al[42] used the fractal dimension to predict clinically significant post-endoscopic bleeding (CSPEB) by analyzing blood vessel morphology within post-colonic endoscopic mucosal resection (EMR) mucosal defects. They introduced the fractal dimension estimate as a measure of the complexity of blood vessel contour, and on multivariate analysis, found that fractal dimension and four other independent variables correlated with CSPEB. This suggests that the morphometric characteristics of blood vessels in post-EMR defects can be used to predict delayed bleeding following colonic EMR. Ren et al[43] measured curvature, fractal dimension, and volumetric feature maps to assist radiologists in reducing interpretation time and improving detection results in computed tomographic colonography.
In their study, Mah et al[34] investigated the use of fractal dimension to distinguish between healthy and cancerous colon images and to examine the relationship between fractal dimension and traditional texture analysis features. They found a highly significant difference between the groups using fractal analysis. Interestingly, they also reported that micro-architectural analysis of the histologically examined colon mucosa provided unprecedented sensitivity for early detection of CRC[34]. They observed significant alterations in spectral slope, fractal dimension, and principal component 3 in mouse mucosa at the earliest time points, and these alterations increased over time, indicating the micro-architectural underpinnings of subsequent tumorigenesis.
Additionally, these indexes spatially correlated with future adenoma development. The concept of “deformability” has been introduced as a hallmark of the CRC process leading to metastatic spread.
Furthermore, Streba et al[44] used fractal analysis to estimate elements obtained from images taken from pathological and immunohistochemical investigations of colonic biopsy fragments in patients who underwent surgery for previously diagnosed CRC. They introduced the concept of “deformability” as a hallmark of the CRC process leading to metastatic spread. The authors performed a fractal analysis using an in-house tool.
Streba et al[44] found that the fractal dimensions were significantly different between adenocarcinomas and other types of colonic cancers, but no significant differences were found between most types of CRCs. They also reported a significant statistical difference when comparing well-differentiated tumors with all other stages. The authors concluded that fractal analysis is a novel and interesting tool for determining the pathologic diagnosis of CRCs, and may further improve diagnostic and prognostic rates, thus enhancing patient care.
Several initial studies have suggested that the novel agent polyethylene glycol (PEG) may have the necessary chemopreventive properties for widespread clinical use[45]. Despite reports attesting to its remarkable efficacy, the mechanisms of action of PEG remain largely unexplored. To determine the stage of carcinogenesis that PEG targets, Roy et al[45] assessed fractal dimension, one of the earliest markers of neoplastic transformation of the colon, in fresh colonic tissue using four-dimensional elastic light-scattering fingerprinting.
Studies have shown that PEG can suppress morphologic variables and restore micro-architectural organization, as indicated by the fractal dimension estimate. Changes in fractal dimension have been observed prior to the development of aberrant crypt foci in azoxymethane-treated rats and adenomas in mouse models, making fractal dimension a sensitive early marker in cancer prevention. Short-term treatment with PEG has been shown to completely normalize fractal dimension, indicating that PEG can reverse the earliest changes of colon carcinogenesis.
Strauss et al[46] assessed the impact of quantitative parameters on the differentiation of primary CRCs from normal colon tissue. They applied compartment and non-compartment modeling to dynamic PET data in 22 patients with CRCs prior to surgery, five of whom also had liver metastases at the time of the PET study. The non-compartment modeling was used to calculate the fractal dimension of the time-activity data. The study found that using quantitative data had the advantage of not being primarily dependent on the individual assessment and experience of the physician visually evaluating the FDG PET data. Additionally, the analysis of dynamic PET data of the corresponding primary tumor could predict the presence of metastatic lesions.
Strauss et al[46] found that the fractal dimension, standardized uptake value, influx, and k3 were the most important single parameters for lesion differentiation[46]. The study also demonstrated that the highest accuracy for lesion differentiation was achieved with the fractal dimension[46]. The use of quantitative data has the advantage that the detection of CRC is not solely dependent on the individual assessment and experience of the physician visually evaluating the FDG-PET data. Quantitative FDG-PET studies provide accurate data for differentiating primary CRCs from natural tissue, and most of these studies conclude that the presence of metastatic lesions can be predicted by analyzing the dynamic PET data of the corresponding primary tumor[46,47].
Studies have found that 18F-FDG kinetics are primarily dependent on the expression of genes associated with glucose transporters and hexokinases, but may also be modulated by other genes. Strauss et al[47] investigated the dependency of 18F-FDG kinetics on angiogenesis-related gene expression. They evaluated a series of 25 patients with primary CRCs using PET and 18F-FDG within 2 d before surgery.
During surgery, tissue specimens were obtained from the tumor and adjacent non-tumoral colon, and gene expression was assessed using gene arrays. Strauss et al[47] identified 23 angiogenesis-related genes with a tumor-to-normal ratio exceeding 1.50, and found a significant correlation between k1 and vascular endothelial growth factor, as well as between fractal dimension and angiopoietin-2. They also noted a negative correlation between k3 and VEGF-B, and a positive correlation for angiopoietin-like 4 gene. In a recent study, Goh et al[48] evaluated the feasibility of using fractal analysis to assess the spatial pattern of CRC perfusion at dynamic contrast-enhanced CT (perfusion CT).
Twenty CRC patients who underwent a 65-second perfusion CT study. A perfusion parametric map was generated using validated commercial software. The tumor was identified by an experienced radiologist, segmented via thresholding, and fractal analysis was applied using in-house software. Fractal dimension, abundance, and lacunarity were assessed for the entire outlined tumor, as well as for selected representative areas within the tumor of low and high perfusion.
The study by Goh et al[48] concluded that fractal values were higher in cancer than in normal colon, and that fractal values were lower in areas of high perfusion compared to low perfusion areas. Lacunarity curves were shifted to the right for cancer compared to normal colon. The results suggest that CRCs mapped by perfusion CT demonstrate fractal properties, and thus fractal analysis is feasible, potentially providing a quantitative measure of the spatial pattern of tumor perfusion.
Lętowska-Andrzejewicz et al[49] have investigated the effects of 5-fluorouracil, interferon, and dexamethasone, on the healing of colon anastomosis by assessing morphometric and fractal parameters of the colonic wall. Lętowska-Andrzejewicz et al[49] performed an experimental anastomosis of the ascending colon in 60 male Wistar rats and subsequently randomly assigned them to four groups. On the second to sixth post-operative days, the rats were administered 5-fluorouracil, interferon-α, dexamethasone, or 0.9% NaCl solution as a control. The healing of the anastomosis was assessed through macroscopic, histomorphometric, and microbiological evaluations. The histomorphometric parameter changes were most evident on the seventh and fourteenth post-operative days in all treatment groups. Connective tissue fractal dimension significantly decreased in those animals treated with interferon and dexamethasone. All three pharmaceutical agents impaired healing of the anastomosis and promoted infection in the anastomosis and skin wound sites. Dexamethasone was considered the most detrimental in this study, as it induced both morphometric and macroscopic alterations.
The inability of cytotoxic anticancer therapies to effectively treat tumors may lead to changes in their morphology and increased tissue invasion. This effect is more prominent in cancer cells with strong metastatic capabilities. Researchers, Pasqualato et al[50], have established a clear correlation between alterations in cell shape and the development of a more aggressive phenotype in colon cancer cells that are resistant to 5-FU treatment, specifically HCT-8FUres.
The observed changes in cell shape were strongly associated with an increase in the speed of cellular movement. Pasqualato et al[50] developed a method to quantitatively measure the shape of both wild-type and chemoresistant HCT-8 cells during a wound healing assay. They assessed various shape descriptors such as the area/perimeter ratio, circularity, roundness, fractal dimension, and solidity to characterize the biological behavior of these two cell lines. Solidity was identified as the most effective parameter for distinguishing between the chemoresistant and wild-type cells. Moreover, this parameter was found to capture the differences in cell shape at each time point of the migration process. Furthermore, a negative correlation was observed between solidity and motility speed.
The fractal pancreas
Studies that attempt to quantitatively analyze the growth and development of pancreatic islets in both normal and pathological conditions have encountered significant challenges in terms of methodology and conceptualization. To address these challenges, Hastings et al[51] conducted a study that utilized the “geometry of random fractals” to investigate the regeneration of islets in guinea pigs that had been treated with alloxan.
The authors of the aforementioned study have since demonstrated that the power-law distribution of pancreatic islets is consistent across various mammalian species and is maintained throughout ontogenetic development in guinea pigs[52]. This suggests that islet formation adheres to an iterative or fractal pattern that is common among mammals. The islets of Langerhans, which are responsible for regulating blood glucose levels, are known to be unevenly distributed throughout the pancreas. In fact, it has been reported that there exists a universal power-law that governs the fractal spatial distribution of islets in two-dimensional pancreatic sections[52].
In a study conducted by Jo et al[53], the three-dimensional spatial distribution of islets in intact mouse pancreata was examined using optical projection tomography. The results showed a power law distribution with a fractal dimension of 2.1. The authors also analyzed two-dimensional pancreatic sections from human autopsies and found that the distribution of human islets followed a universal power law with a fractal dimension of 1.5 in adult pancreata. This value is consistent with previous findings in smaller mammalian pancreas sections. Finally, the authors developed a growth model to explain the development of islet distribution and suggested that the fractal nature of the spatial islet distribution may be due to self-avoidance in the branching process of vascularization in the pancreas[53].
Pancreatic cancer is a highly aggressive disease with a poor prognosis, despite surgical intervention. To improve patient outcomes and avoid unnecessary laparotomies, it is crucial to identify reliable factors that can predict the resectability of pancreatic tumors. Vasilescu et al[54] conducted a study to determine if nuclear morphometry and fractal dimension of pancreatic nuclear features could serve as preoperative indicators for assessing pancreatic resectability. The study involved sixty-one patients diagnosed with pancreatic cancer, who were divided into two groups: those with resectable cancer and those with non-resectable pancreatic cancer. The authors evaluated several morphometric parameters, including nuclear area, length of minor and major axes, and nuclear shape and chromatin distribution of pancreatic tumor cells, which were estimated using fractal dimension analysis. The morphometric analysis conducted by Vasilescu et al[54] revealed significant differences in the nuclear area between the resectable and non-resectable groups. The non-resectable group was also found to have a higher value of fractal dimension in both nuclear outlines and chromatin distribution. Based on these findings, the authors suggested that objective measurements should be utilized to enhance risk assessment and treatment decision-making for pancreatic cancer. Additionally, they proposed that the fractal dimension of nuclear shape and chromatin distribution could be a valuable tool for conventional pathological analysis. In another study, fractal analysis was used to demonstrate that ghrelin administration increased structural complexity and tissue disorder in rat exocrine pancreas[55].
The study involved 40 male Wistar rats, where pancreas tissue sections were stained with hematoxylin and eosin and visualized through light microscopy. The average values of tissue fractal dimension, lacunarity, and co-occurrence matrix texture parameters were determined for each animal using computer-aided image analysis. The authors found that regardless of age, administration of ghrelin increased the fractal dimension and textural entropy of the exocrine pancreas, while decreasing its lacunarity. This is the first study to examine the effects of ghrelin on the morphological properties of pancreatic tissue and the first to utilize fractal and textural analysis methods to quantify the architecture of exocrine pancreas tissue.
According to Metze[56], fractal characteristics of chromatin have been identified through light or electron microscopy in the past 20 years. These features can be easily estimated from digitized microscopic images and are useful for cancer diagnosis and prognosis. Studies have shown that an increase in the fractal dimension of stained nuclei occurs during carcinogenesis and tumor progression in various cancers, including pancreatic cancer. Researchers have also reported potential connections between changes in chromatin organization during carcinogenesis and tumor progression and an increase in the fractal dimension of stained chromatin.
The fractal dimension of chromatin in routine histological or cytological preparations has been found to increase during various stages of tumor development, including from pre-neoplastic stages to cancer, and from initial cancer stages to advanced stages. Additionally, higher fractal dimensions are associated with poor prognosis, while lower fractal dimensions are observed in patients with a better prognosis. Al-Mrabeh et al[57] conducted a study to determine whether the low volume and irregular border of the pancreas in patients with type-2 diabetes could be normalized following the reversal of diabetes.
The study conducted by Al-Mrabeh et al[57] utilized three-dimensional volume-rendering and fractal dimension analysis of MRI-acquired images, along with three-point Dixon imaging to measure fat content. The results indicated no change in pancreas volume six months after diabetes reversal compared to baseline. However, the reversal of diabetes was associated with an increase in the irregularity of pancreas borders between baseline and eight weeks, followed by a decrease at six months. In contrast, no changes in fractal dimension were observed in the non-reversed group. The authors concluded that combining three-dimensional volume segmentation of the pancreas with fractal dimension analysis could provide a promising mathematical definition of the pancreas border morphology.
Fractal dimension analysis revealed a significant increase in pancreas complexity after acute weight loss in the responder group, followed by a significant decrease resulting in a smoother pancreas border by the end of the study. Conversely, no changes in the pancreas border were observed in the non-responder group. Although the effect of insulin on the endocrine pancreas has been extensively studied, there have been few quantitative morphometric investigations of the exocrine pancreas. Recently, Pajevic et al[58] conducted a study to investigate the effect of acute and chronic insulin administration on the morphology of rat pancreas acini. The results showed that acute insulin treatment, regardless of the applied doses, increased the fractal dimension of the pancreas acini while decreasing their lacunarity.
The study showed that chronic low-dose insulin treatment decreased the fractal dimension and increased the lacunarity of pancreas acini, whereas high-dose insulin had the opposite effect. These findings suggest that fractal analysis could be used to detect fine architectural changes in acini, making it a potential alternative or addition to routine stereology.
In recent years, endoscopic ultrasound (EUS) elastography has been demonstrated as a useful technique for characterizing solid pancreatic lesions (SPLs). Carrara et al[59] introduced a combined analysis using EUS elastography (strain ratio) and fractal analysis to characterize the morphology of SPLs. A total of 102 SPLs from 100 patients were analyzed, and the results showed that both the parenchymal strain ratio (pSR) and wall strain ratio (wSR) were significantly higher in malignant SPLs than benign ones during elastography.
Fractal analysis revealed a significant difference in mean surface fractal dimensions between malignant lesions and neuroendocrine tumors, suggesting that combining EUS elastography with pSR and fractal-based analysis is a promising method for quantitatively characterizing SPLs[60].
It is widely accepted that the desmoplastic reaction is a hallmark of pancreatic cancer, although its impact on tumor behavior remains debated. Grizzi et al[61] recently developed a computer-aided method for quantifying the amount of pancreatic collagenic ECM, its spatial distribution pattern, and its degradation process.
The study conducted by Grizzi et al[61] demonstrated a progressive increase in pancreatic collagenic ECM from normal to inflammatory and pancreatic ductal adenocarcinoma. The two-dimensional fractal dimension revealed a significant difference in the spatial complexity of collagenic ECM between normal and inflammatory and pancreatic ductal adenocarcinoma. Moreover, a significant difference was observed when comparing the number of cycles required to degrade pancreatic collagenic ECM in normal vs inflammatory and pancreatic ductal adenocarcinoma. The mean velocity of collagenic ECM degradation was also found to be faster in inflammatory and pancreatic ductal adenocarcinoma than in normal. These findings highlight the potential of computer-aided methods and fractal analysis in quantifying the pancreatic ECM and its role in pancreatic diseases.
The study has demonstrated that inflammatory and pancreatic ductal adenocarcinomas are characterized by an increased amount of pancreatic collagenic ECM, as well as changes in its spatial complexity and degradation. These findings define new features of the pancreatic collagenic ECM and provide a basis for further investigations into the clinical behavior of pancreatic ductal adenocarcinoma and the development of therapeutic strategies. Overall, the study highlights the potential of computer-aided methods and fractal analysis in quantifying the pancreatic ECM and its role in pancreatic diseases, ultimately contributing to improved diagnostic and therapeutic approaches for patients with pancreatic cancer.
Recently, researchers investigated the relationship between ductal morphometry and ramification patterns in the submandibular gland and pancreas to confirm their shared fractal dimension[62]. The study found that while the length of the intraglandular submandibular duct and the main pancreatic duct were correlated, other morphometric features of the ducts were not. This suggests a more intricate relationship between the two digestive glands beyond a simple shared fractal dimension.
Fractal analysis offers maps of the FD, which allows for a more dependable and size-independent measurement utilizing gross pathology or multi-parametric MRI as reference standards[63]. This approach quantifies perfusion chaos, the underlying pathophysiological principle, and can differentiate the more chaotic tumor rim from the tumor core and nearby non-tumorous pancreatic tissue.
Abdominal CT biomarkers, both inside and outside the pancreas, have the potential to diagnose type 2 diabetes mellitus. Tallam et al[64] conducted a study on a large clinical dataset using fully automated deep learning to investigate abdominal CT biomarkers for type 2 diabetes mellitus. Their findings revealed that the most accurate predictors of type 2 diabetes mellitus include intrapancreatic fat percentage, pancreatic fractal dimension, plaque severity between the L1 and L4 vertebra levels, average liver CT attenuation, and BMI.
The fractal liver
In 1989, Dioguardi[65-67] (1921-2019) proposed the liver as a composite system comprised of a set of operative microunits that receive a continuous flow of matter, energy, and information. The development of mathematical models for non-Euclidean geometry has led to the creation of models for highly complex natural phenomena[68]. In developmental biology, branching morphogenesis has been explained through self-similar iterative branching rules that have helped to elucidate branch patterns observed in various tissue types. However, in solid viscera, the issue of geometry is more complex, as there is no readily available marker for geometry in parenchymal tissue. The mosaic pattern provides such a marker for studying solid viscera.
The patches observed in mosaic liver have been shown to exhibit fractal properties, indicating that the pattern may have arisen from a self-similar process in which small areas are representative of, although not necessarily identical to, the whole object. This observation provides a new analytical approach to the study of biological structure in organogenesis[68]. It is well-established that partial hepatectomy induces compensatory, non-neoplastic growth and regeneration in mammalian liver[69]. Previous experimental evidence has suggested that compensatory liver growth occurs uniformly, without focal centers of proliferation. Given this information, fractal analysis was used to test various hypothesized patterns of regenerative growth in the liver. The results of this analysis indicate that the mosaic pattern does not change significantly during the regenerative process. The area and perimeter of patches (the area occupied by or perimeter around cells of like lineage) increase during compensatory liver growth in chimeric rats without altering the geometric complexity of patch boundaries (the boundaries around cells of like lineage). These tissue findings are consistent with previously reported computer models of growth in which repetitive application of simple decisions assuming uniform growth created complex mosaic patterns.
These findings support the idea that an iterating, self-similar cell division program is sufficient for the regeneration of liver tissue following partial hepatectomy. Such programs are important because they suggest a way in which complex patterns, or morphogenesis, can be efficiently created from a small amount of stored information. In geometrical terms, liver fibrosis is an example of self-similar natural fractal structure[70].
To evaluate the usefulness of a reliable and reproducible mathematical scoring system based on fractal geometry for quantifying the irregular pattern in fibrosis commonly seen in liver biopsy specimens from chronic liver diseases, Dioguardi et al[70] investigated 26 liver biopsy sections obtained from patients with chronic hepatitis C virus-related liver disease. The degree of fibrosis in each section was estimated using a quantitative scoring system based on the computer-assisted evaluation of both the fractal and spectral dimensions of deposited collagen. The findings indicated that the fractional dimension of its irregular shape defines fibrosis as a natural fractal structure.
The study by Dioguardi et al[70] proposed a method for quantifying irregular patterns in liver tissue using fractal geometry. The method is based on a quantitative scoring system that evaluates the fractal and spectral dimensions of collagen deposited in liver biopsy sections obtained from patients with chronic hepatitis C virus-related liver disease. The results showed that the fractional dimension of the irregular shape of fibrosis defines it as a natural fractal structure, and a single numerical score can be used to quantify the complex distribution of collagenous components. The method is reproducible, rapid, and inexpensive, and eliminates subjectivity and external factors that can influence staging and classification. The method uses a rectified meter implemented in a computer-assisted planar image analysis system to give metric measures of irregular outlines and surfaces, which can be used to produce an index that quantifies the typical wrinkledness of biologic objects[71]. A computer-aided morphometric method employing fractal geometry and Delaunay triangulation was introduced to quantify the necro-inflammatory phase in liver biopsy specimens. The method was applied to two-micrometer thick sections from 78 chronic hepatitis C virus-infected patients, immunohistochemically treated to identify inflammatory cells[62]. An automatic image analysis system was used to define the inflammatory cell network based on Delaunay triangulation, and the cells were categorized geometrically into clusters or irregular distributions within the tissue. This automatic method is fast and objective, producing accurate results represented by scalar numbers and allowing the organ’s condition to be represented by Hurst’s exponent with an error of no more than 12%. The availability of precise measurements and a reasonably representative assessment of the organ’s overall state raises questions about revising the indications for hepatic biopsy, taking into account its invasiveness and subjective interpretation. A computer-aided method utilizing fractal principles was applied to digitized histological biopsy sections from 209 patients with varying degrees of chronic hepatitis C virus-related fibrosis or cirrhosis[72]. This model offers the first metric evaluations of fibrosis’s geometric properties and quantitative liver tissue architectural changes[72]. To evaluate the sampling variability of computer-aided, fractal-corrected fibrosis measurements in liver biopsies, Grizzi et al[73] examined samples from different liver parts removed from 12 patients with clinically and histologically proven cirrhosis who underwent orthotopic liver transplantation. A computer-aided image analysis system automatically measured fibrosis surface, perimeter, fractal surface and dimensions, wrinkledness, and Hurst coefficient in Sirius red-stained sections. High inter-sample variability was found in fibrosis surface and wrinkledness measurements, while Hurst’s exponent variability was low. The study suggests that Hurst’s exponent is a valuable histological estimate of fibrosis in the entire organ for clinical use, emphasizing the crucial role biopsy sections play in qualitatively diagnosing chronic hepatitis and quantitatively estimating architectural changes in liver tissue.
A technique for analyzing liver biopsy samples was proposed, which involves the use of the “Dioguardi Histological Metriser” machine to automatically measure various parameters related to liver health, including residual hepatocyte mass, inflammation, fibrosis, and loss of liver tissue tectonics[74]. This technique was validated by analyzing digitized images of liver biopsy sections from 398 patients and comparing the results to a semi-quantitative scoring system. The method provides measurements for the extent of hepatocyte mass, including abnormal lipid accumulation; the size of the inflammation basin and the number of leukocytes within it; the degree of collagen islets, which are classified into three magnitudes; and the tectonic index, which quantifies the degree of liver tissue organization disorders.
The findings of the proposed technique represent the first standardized method for measuring the geometric properties of liver tissue, including parenchyma, inflammation, fibrosis, and tectonics of biopsy sections. Other authors have also reported on the accuracy and feasibility of using fractal analysis to measure liver fibrosis. A study involving 77 rats, including 10 sham, 46 with fibrosis due to bile duct ligation, and 21 with fibrosis resulting from CCl4 intoxication, was conducted to investigate various measurements, such as the fractal dimension of Kolmogorov, histologic lesions, the area of fibrosis by image analysis, liver hydroxyproline content, messenger RNA fibronectin, serum hyaluronate level, and portal pressure[75]. The results showed that the fractal dimension of Kolmogorov was correlated with other markers of fibrosis, including the area of fibrosis, hydroxyproline content, serum hyaluronate level, and portal pressure.
The study found that the fractal dimension of Kolmogorov was significantly different between the two fibrosis models, unlike the area of fibrosis, and this relationship was independent of other histologic lesions. These results suggest that fractal analysis is an appropriate technique for analyzing liver fibrosis and has excellent reproducibility. In fact, this method is the only quantitative morphometric approach that can distinguish between different fibrosis models and is sensitive enough to detect pharmacologically-induced changes in liver fibrosis. Meanwhile, Fibroscan is a widely used technique for assessing liver fibrosis in chronic hepatitis C by measuring liver stiffness. However, it remains unclear how liver steatosis, which is a common feature of chronic hepatitis C and other chronic liver diseases, affects the accuracy of liver stiffness evaluation (LSE).
A quantitative morphometric analysis was conducted on 650 patients with chronic hepatitis C who underwent liver biopsy and LSE. The liver specimens were evaluated using both optical analysis (Metavir F and A, steatosis grading) and computerized morphometry to determine the area and fractal dimension of liver fibrosis and steatosis. The precise evaluation of liver histology using computerized morphometry revealed that liver stiffness measured by Fibroscan was associated with liver fibrosis, activity, and steatosis. In cases of high levels of steatosis, Fibroscan measurements may result in misinterpretation of liver fibrosis. Meanwhile, Nielsen et al[76] used a polygonization-based method to estimate the fractal dimension and other scalar lacunarity features from digitized transmission electron micrographs of mouse liver cell nuclei.
The aim of Nielsen et al[76] was to determine whether a small set of fractal features could differentiate between natural liver samples, hyperplastic nodules, and hepatocellular carcinomas (HCC). They found that several single fractal features estimated from the periphery of the cell nuclei could distinguish between samples from hyperplastic nodules and HCC and those from normal liver tissue. Recent studies suggest that the cellular environment’s mechanical influences can have significant effects on gene activity, cell differentiation, and proliferation, in addition to chemical factors[77]. These mechanisms involve a tissue matrix system that includes the ECM, nuclear matrix, and cytoskeleton. As hepatocytes during fetal development are a useful model for studying such variations, Vassy et al[77] investigated hepatocyte differentiation from fetal to adult livers using computerized quantitative image analysis of cytokeratin 8 immunofluorescent localization.
Vassy et al[77] investigated a set of line features, including the number and length of lines, orientation of lines, and the fractal dimension of the filament network, to analyze hepatocyte differentiation from fetal to adult livers. The study found highly significant differences in the features studied throughout liver development, including an increase in the total amount of cytokeratin filaments, demonstrating the feasibility of objective and quantitative analysis of the differences in the pattern of the cytokeratin filament network. Meanwhile, the organization of the hepatic microvascular network has been widely studied in recent years, particularly in cirrhosis. A quantitative mathematical approach based on fractal and Fourier analyses performed on photomicrographs has been used to recognize the distinctive vascular patterns in cirrhotic livers compared to natural livers[78]. The study found that the natural hepatic sinusoidal network had higher complexity than the cirrhotic network, with more significant morphological changes observed in rats with bile duct-ligation cirrhosis than those with CCl4-induced cirrhosis. These findings could provide insight into the pathophysiological alterations of the liver and may have diagnostic value in future clinical research. Additionally, aging-related modifications have been shown to cause marked changes in both the structure of the liver sinusoidal endothelial cell and liver perfusion[79]. Fractal and Fourier analyses and micro-CT showed that age did not affect sinusoidal dimensions, sinusoidal density, or dispersion number, but there were changes in the geometry and complexity of the sinusoidal network as determined by fractal dimension and degree of anisotropy.
Small age-related changes in the architecture of the liver sinusoidal network can influence hepatic function and may reflect broader aging changes in the microcirculation. Fractal analysis has been applied to HCC as well[80-83]. The fractal dimension has been investigated as a quantifier of non-Euclidean two-dimensional vascular geometry in a series of paired specimens of primary HCC and surrounding non-tumoral tissue. Blood vessels had a higher fractal dimension in primary tumors compared to liver metastasis, and this approach allowed for differentiation between primary liver tumors with and without neurodifferentiation. Fractal geometry has also been used to investigate alpha-fetoprotein behavior in patients with HCC waiting for liver transplant[84]. Furthermore, it has been shown that the chromatin of mouse hepatocytes exhibits age-related reduction of fractal dimension, suggesting that this index can be a potential indicator of age-associated changes in chromatin structure[83].
The study of fractal architecture in various organs and structures has expanded the possibilities for determining their functioning and structural arrangement, leading to the development of new approaches to diagnostics and therapeutic interventions. Recently, Azmaiparashvili et al[85] investigated the spatial geometry of the biliary tree and assessed the significance of both its fractal and Euclidean characteristics for developing approaches that provide a comprehensive description of intrahepatic biliary tract architecture. This configuration of the biliary bed is essential for ensuring the smooth implementation of the physiological function of the liver and its adaptation to different pathologies accompanied by biliary hypertension. Furthermore, the findings could be considered in the diagnosis and assessment of ductular reaction, biliary regeneration, and/or carcinogenesis.
There is a growing interest among researchers in employing fractal geometry-based algorithms for modeling, monitoring, and treating hepatitis B virus infections, as comprehending the intricate relationships between pathogens, immune systems, and overall liver function is of vital importance[86].
Recently, fractal geometry has been employed to model portal hypertension[87]. Specifically, the model encompasses the entire process of blood flow, starting from the sinusoids and culminating in the portal vein. It can be adjusted to account for the diagnosis of portal hypertension caused by thrombosis and liver cirrhosis. Moreover, this approach offers a novel way to detect portal vein pressure noninvasively from a biomechanical perspective. Furthermore, the combination of qualitative MRI features with fractal analysis has enabled the identification of subtypes of hepatocellular adenomas HCCs in patients with non-cirrhotic livers[88]. This approach also enhances the differentiation of lesions with a high-risk of malignant transformation from those with a low-risk[88]. Liver and tumor segmentation from CT scans plays a critical role in hepatic surgical planning. As manual segmentation is both time-consuming and labor-intensive, a fully automated approach is highly sought after. Chen et al[89] introduced an automatic two-step liver and tumor segmentation method. Full-field optical coherence tomography (FF-OCT) has been recognized for its label-free subcellular imaging capabilities. Recently, Zhu et al[90] demonstrated the promise of their classifier using FF-OCT images for label-free, quantified tumor detection. This suggests that a fractal dimension-based classifier could potentially assist clinicians in identifying tumor boundaries for surgical resection in the future.