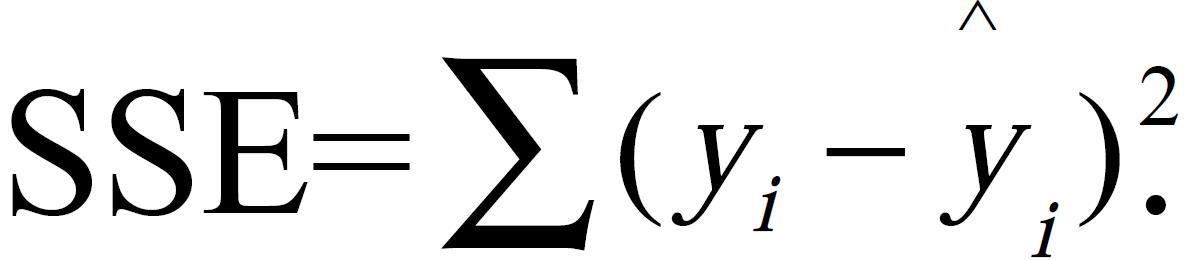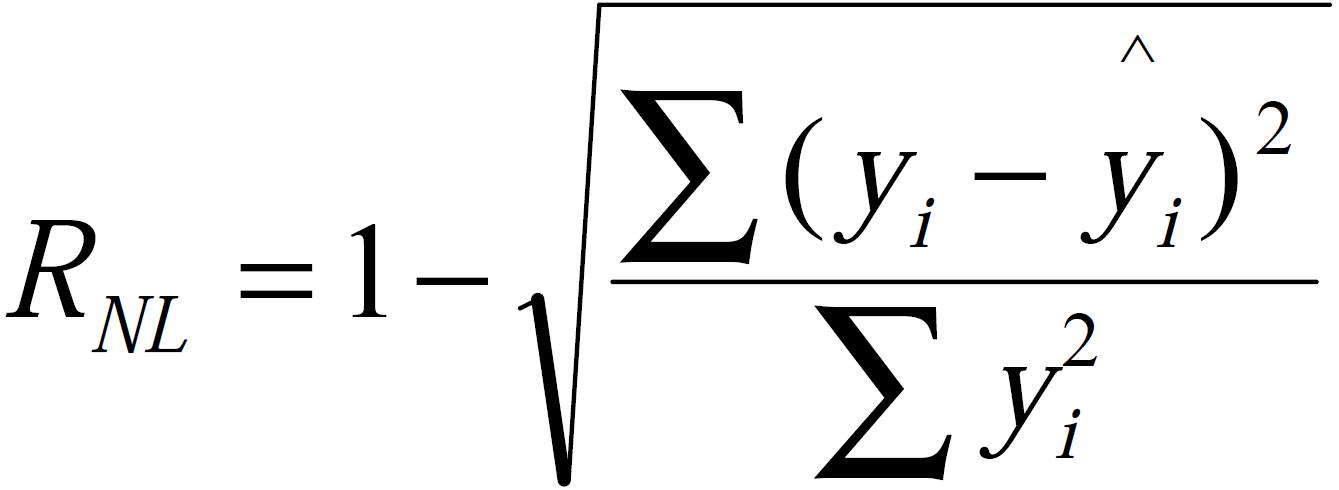Published online Dec 15, 2004. doi: 10.3748/wjg.v10.i24.3579
Revised: May 2, 2004
Accepted: May 9, 2004
Published online: December 15, 2004
AIM: To study the application of artificial neural network (ANN) in forecasting the incidence of hepatitis A, which had an autoregression phenomenon.
METHODS: The data of the incidence of hepatitis A in Liaoning Province from 1981 to 2001 were obtained from Liaoning Disease Control and Prevention Center. We used the autoregressive integrated moving average (ARIMA) model of time series analysis to determine whether there was any autoregression phenomenon in the data. Then the data of the incidence were switched into [0,1] intervals as the network theoretical output. The data from 1981 to 1997 were used as the training and verifying sets and the data from 1998 to 2001 were made up into the test set. STATISTICA neural network (ST NN) was used to construct, train and simulate the artificial neural network.
RESULTS: Twenty-four networks were tested and seven were retained. The best network we found had excellent performance, its regression ratio was 0.73, and its correlation was 0.69. There were 2 input variables in the network, one was AR(1), and the other was time. The number of units in hidden layer was 3. In ARIMA time series analysis results, the best model was first order autoregression without difference and smoothness. The total sum square error of the ANN model was 9090.21, the sum square error of the training set and testing set was 8377.52 and 712.69, respectively, they were all less than that of ARIMA model. The corresponding value of ARIMA was 12291.79, 8944.95 and 3346.84, respectively. The correlation coefficient of nonlinear regression (RNL) of ANN was 0.71, while the RNL of ARIMA linear autoregression model was 0.66.
CONCLUSION: ANN is superior to conventional methods in forecasting the incidence of hepatitis A which has an autoregression phenomenon.
- Citation: Guan P, Huang DS, Zhou BS. Forecasting model for the incidence of hepatitis A based on artificial neural network. World J Gastroenterol 2004; 10(24): 3579-3582
- URL: https://www.wjgnet.com/1007-9327/full/v10/i24/3579.htm
- DOI: https://dx.doi.org/10.3748/wjg.v10.i24.3579
Hepatitis A is an important infectious disease in the world[1-4]. Guidelines of vaccination versus hepatitis A call for correct estimation of the incidence of hepatitis A[5-9]. The occurrence of infectious diseases has its rules, affected by the speed of pathogen variation, susceptible accumulation and environmental changes. Early recognition of the epidemic rules is significantly important for the prevention and control of hepatitis. Among the available models, time series analysis[10,11] and regression analysis[12-14] are poorly suited for discovering the epidemic rules. The reason for this lies in the complexity of their relationship.
However, artificial neural networks (ANN) can recognize the rules to make right prediction and provide assistance for decision-making because they have the characteristics of self-organizing and self-learning processes[15-18]. Artificial neural networks are computation systems that process information in parallel, using a large number of simple units, and that excel in tasks involving pattern recognition. These intrinsic properties of the neural networks have been translated into higher performance accuracy in outcome prediction compared with expert opinion or conventional statistical methods[19-22].
Recently, backpropagation (BP) artificial neural network has been widely applied to a variety of problems in the field of medicine[23-26]. It is also called the front forward network because it is the front forward error propagation network without feedback. There is no mutual connection among the neurons in the same layer.
In the present work, we applied several artificial neural networks to the forecast of the incidence of hepatitis A. We also represented the basic principles and how to train the neural networks.
The data of the incidence of hepatitis A in Liaoning Province from 1981 to 2001 were obtained from Liaoning Disease Control and Prevention Center. The highest incidence of hepatitis A during this period was 160.07 per one hundred thousand, and then the incidence descended progressively from 1981-1986 and rose from 1986 to 1989 (Figure 1). The low incidence could be seen from 1996. To switch these data into [0,1] intervals, we applied the following transformation: the network theoretical output was equal to the incidence of hepatitis A/200 by using 1/105 as the unit of measurement.
Automatic network designer The automatic network designer determined a suitable architecture, using a combination of heuristics and sophisticated optimization strategies. It conducted a large number of tests, which were used to determine the best architecture. It could automatically compare linear, probabilistic neural network (PNN), generalized regression neural network (GRNN), radial basis function and multilayer perceptron networks (Figure 2), and automatically choose the smoothing factor for PNN or GRNN, the smoothing factor and the number of units for radial basis function networks, and the number of units for multilayer perceptrons. We could control the length and rigor of search iteration to be performed, and bias the search towards smaller networks using a unit penalty factor.
Intelligent problem solver In ST NN, an intelligent problem solver was used to select the most excellent network. We chose the advanced version to customize the design process, the problem needed to be solved was a time series problem. Because many time series had a natural period, steps parameter equals to 1 was indicated here by ARIMA analysis. The output variables were transformed values of incidence of hepatitis A, and the input variables were time and AR (1) which meant former transforming values. The software could search for a useful subset of the specified variables. The cases in the data set were divided into three subsets, one for training the network, one for cross verification and the last one for testing. In practice, the data from 1981 to 1992 were used to train the network and the data from 1993 to 1997 were used as a verifying set. The performance of the network could be tested by estimating the data from 1998 to 2001.
Four types of networks, such as linear network, multilayer perceptron (3 layers), probability network or GRNN and radial basis function, needed to be considered. In the mean time, network complexity was determined automatically. A medium length of design procedure was selected, which conducted a fast search for an optimal network. The network saved would be one with balance performance against types and complexity. The best network found (taking account of diversity) was retained.
Choosing the number of hidden layers and units was the most critical problem. There were a few heuristics that could guide here. One hidden layer was sufficient for most problems when multilayer perceptrons were used. If the error could not be gotten down to an acceptable level even with a large number of hidden units, it might be worth trying two hidden layers.
A large number of hidden units could generally model a more complex problem, but required more training and were more prone to poor generalization. The changes in training and verification errors should be observed as the experiment was being done. If the addition of more hidden units caused a decrease in both, then the network was probably too small. However, if the verification error was significantly larger than the training error and, in particular, if it deteriorated during iterative training, then the network was probably too large.
The number of weights and thresholds in the network should be less than or much less than the number of training cases. Ideally, there should be about two to five as many training cases as weights. If the number of training cases was small, the smaller networks should be used because of no enough data to model a complex function. If the cases were fewer than the product of the number of inputs and outputs, only a linear model should be used. Lack of sufficient data was one reason why it was sometimes good to remove input variables. Even if the variables had some genuine information, the reduction in network size consequent upon removing them might improve network performance.
One index to evaluate the performance of networks and ARIMA was sum square of error (SSE):Math 1. The other was nonlinear determinant coefficient: Math 2, where yi is the real value of case i and ^yi is the estimated value of case i.
Math 1
Math 2
Finally 24 networks were tested, and 7 were retained. The best network we found was BP network, which had excellent performance, its regression ratio was 0.73, and its correlation was 0.69.
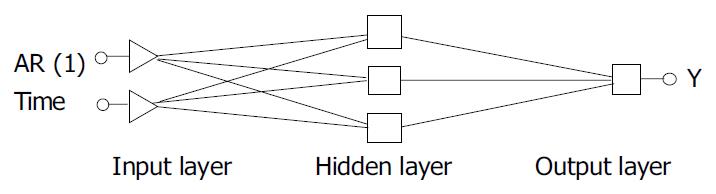
The structure of the network is shown in Figure 3. There were 2 input variables, one was AR (1), the other was time. The number of units in hidden layer was 3. The weight and threshold distribution of the best network is shown in Table 1.
| Unit 1 | Unit 2 | Unit 3 | Y | |
| Threshold | 0.9607 | 1.0829 | 0.6224 | 0.4850 |
| AR (1) | 0.2390 | 0.7930 | 1.0584 | |
| Time | 0.4902 | 0.4344 | 0.4156 | |
| Unit 1 | 0.5281 | |||
| Unit 2 | 0.7572 | |||
| Unit 3 | 1.0723 |
In ARIMA time series analysis results, the best model was first order autoregression without difference and smoothness. The coefficient of AR (1) and constant were 0.83 and 81.22, respectively (Table 2).
| Variables | Coefficient | SE of coefficient | t | P |
| AR (1) | 0.83 | 0.12 | 6.88 | 5.27 × 10-6 |
| Constant | 81.22 | 30.94 | 2.62 | 1.91 |
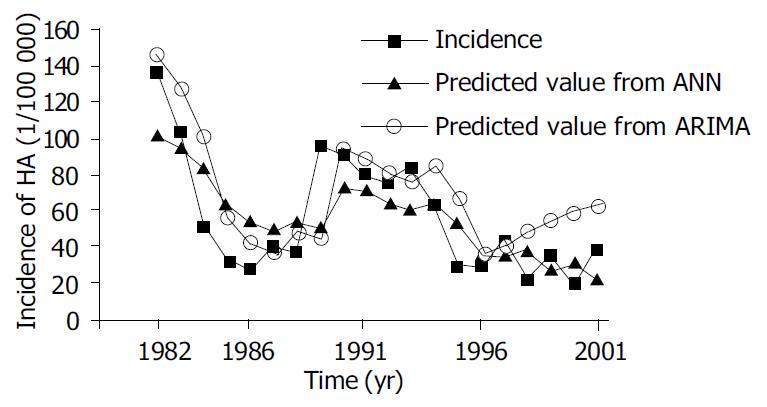
The goal of training the network was to compare the performance with conventional methods by using inverse transforming predicted value obtained from the network. Predicted value and error are shown in Table 3, and its corresponding line graph is shown in Figure 4.
| Time (yr) | Incidence (1/100000) | Predicted value from ANN | Error from ANN | Predicted value from ARIMA | Error from ARIMA |
| 1981 | 160.07 | - | - | - | - |
| 1982 | 136.68 | 101.58 | 35.10 | 146.87 | -10.19 |
| 1983 | 104.12 | 94.63 | 9.49 | 127.39 | -23.27 |
| 1984 | 50.50 | 83.87 | -33.37 | 100.29 | -49.79 |
| 1985 | 32.99 | 62.34 | -29.35 | 55.65 | -22.66 |
| 1986 | 26.74 | 53.26 | -26.52 | 41.07 | -14.33 |
| 1987 | 39.94 | 49.11 | -9.17 | 35.86 | 4.08 |
| 1988 | 36.75 | 53.72 | -16.97 | 46.85 | -10.10 |
| 1989 | 96.92 | 50.42 | 46.50 | 44.20 | 52.72 |
| 1990 | 91.33 | 73.84 | 17.49 | 94.29 | -2.96 |
| 1991 | 79.52 | 70.90 | 8.62 | 89.64 | -10.12 |
| 1992 | 75.31 | 64.60 | 10.71 | 79.81 | -4.50 |
| 1993 | 85.57 | 61.39 | 24.18 | 76.30 | 9.27 |
| 1994 | 62.54 | 64.00 | -1.46 | 84.84 | -22.3 |
| 1995 | 28.23 | 52.11 | -23.88 | 65.67 | -37.44 |
| 1996 | 29.14 | 35.20 | -6.06 | 37.11 | -7.97 |
| 1997 | 42.90 | 34.36 | 8.54 | 37.86 | 5.04 |
| 1998 | 21.25 | 38.01 | -16.76 | 49.32 | -28.07 |
| 1999 | 34.36 | 27.27 | 7.09 | 54.66 | -20.30 |
| 2000 | 19.31 | 30.87 | -11.56 | 59.11 | -39.80 |
| 2001 | 39.09 | 22.88 | 16.21 | 62.81 | -23.72 |
The total sum square error of the ANN model was 9090.21, the sum square error of the training set and testing set was 8377.52 and 712.69, respectively, while the corresponding value of ARIMA was 12291.79, 8944.95 and 3346.84, respectively. The nonlinear determinant coefficient of ANN and the ARIMA linear autoregression model was 0.71 and 0.66, respectively.
From the above results, we can see that there was a first order autoregression phenomenon in the linear autoregression model. The nonlinear determinant coefficient of the ARIMA linear autoregression model was 0.66. The regression graph shows that there was an obvious linear tendency, but some values were still not perfectly fitted. Differences in the amount were great between values. The sum square error of the model was 12291.79, the sum square error of the training set and testing set was 8944.95 and 3346.84, respectively. While in the model based on artificial neural networks, the nonlinear determinant coefficient was 0.71, higher than that of linear autoregression model. The sum square error of the ANN model was 9090.21, the sum square error of the training set and testing set was 8377.52 and 712.69, respectively. In time series analysis, there was statistical significance in the test of coefficients, showing the existence of first order autoregression. Values from extrapolation forecasting based on ANN were mainly in concordance with the actual values, while values from ARIMA model forecasting were a little higher than the actual values of the incidence. These findings showed that ANN could recognize some rules by preliminary learning, but the effect of some special values over considering sum square error made the forecasting of low incidence inaccurate. Combined application of the traditional methods and artificial neural networks can make use of each other’s merits and raise the right prediction level.
Forecasting the incidence of infectious diseases is very important for their prevention and control. Solving this problem calls for the ability to learn the unknown mapping or function only by the existing examples[27,28]. However, after the mapping or a similar one is learned, artificial neural networks can be used to estimate the mapping when only several parts are known. Now artificial neural networks have been widely accepted as a potentially useful way in modeling complex nonlinear and dynamic systems[29-31]. Neural networks could remove neither the need for knowledge nor prior information about the systems of interest[32]. They just reduce the model’s reliance on the prior information while totally removing the need for the model builders to correctly specify the precise functional forms of the relationship that the model seeks to represent[33]. In addition, they offer real prospects for a cheaper, more flexible, less assumption-dependent and adaptive methodology.
Generally, there are two major ways to train the networks, one seeking high accuracy, and the other considering both the accuracy and performance. Through the former method, mapping was input from N-dimensional space and output to M-dimensional space. Thus, the phenomenon of overlearning occurred and the results of extrapolation were not perfect[34]. In the present work, we divided the original data into three parts, one for training, one for verification, and one for extrapolation and prediction. Thus the problem of overlearning was solved effectively. Time series analysis showed that there was a first order autoregression phenomenon in the data without exponent smoothing. Autoregression phenomenon might often exist in the data of the incidence. Traditional method of solving this is time series analysis[35]. However, it is difficult to practice because it requires to meet several conditions, such as white noise[36]. There are no such limitations in artificial neural network, and the software could voluntarily choose appropriate order of autoregression to fit and predict. In addition, RNL has shown that it is reasonable to employ artificial neural networks in modeling complex nonlinear data.
In conclusion, ANN is likely to be an effective tool in processing time series data. The construction and explanation of the model should be further explored.
Edited by Kumar M and Wang XL Proofread by Xu FM
| 1. | Sitarska-Gołebiowska J, Bielak A. [Hepatitis A in Poland in 2001]. Przegl Epidemiol. 2003;57:129-134. [PubMed] |
| 2. | Lee MB, Middleton D. Enteric illness in Ontario, Canada, from 1997 to 2001. J Food Prot. 2003;66:953-961. [PubMed] |
| 3. | Steinke DT, Weston TL, Morris AD, MacDonald TM, Dillon JF. Epidemiology and economic burden of viral hepatitis: an observational population based study. Gut. 2002;50:100-105. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 23] [Cited by in RCA: 25] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 4. | Mel'nichenko PI, Muzychenko FV, Esaulenko NB, Demenev VI, Podlesnyĭ IV. [Prophylaxis of viral hepatitis A in troops of the North-Caucasian Military District]. Voen Med Zh. 2001;322:49-53, 96. [PubMed] |
| 5. | Wong KH, Liu YM, Ng PS, Young BW, Lee SS. Epidemiology of hepatitis A and hepatitis E infection and their determinants in adult Chinese community in Hong Kong. J Med Virol. 2004;72:538-544. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 32] [Cited by in RCA: 31] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 6. | Jenson HB. The changing picture of hepatitis A in the United States. Curr Opin Pediatr. 2004;16:89-93. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 24] [Cited by in RCA: 26] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 7. | Lolekha S, Pratuangtham S, Punpanich W, Bowonkiratikachorn P, Chimabutra K, Weber F. Immunogenicity and safety of two doses of a paediatric hepatitis A vaccine in thai children: comparison of three vaccination schedules. J Trop Pediatr. 2003;49:333-339. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 13] [Cited by in RCA: 14] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 8. | Péchevis M, Khoshnood B, Buteau L, Durand I, Piquard Y, Lafuma A. Cost-effectiveness of hepatitis A vaccine in prevention of secondary hepatitis A infection. Vaccine. 2003;21:3556-3564. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 14] [Cited by in RCA: 14] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 9. | Averhoff F, Shapiro CN, Bell BP, Hyams I, Burd L, Deladisma A, Simard EP, Nalin D, Kuter B, Ward C. Control of hepatitis A through routine vaccination of children. JAMA. 2001;286:2968-2973. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 90] [Cited by in RCA: 90] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 10. | Fung KY, Krewski D, Chen Y, Burnett R, Cakmak S. Comparison of time series and case-crossover analyses of air pollution and hospital admission data. Int J Epidemiol. 2003;32:1064-1070. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 55] [Cited by in RCA: 65] [Article Influence: 3.1] [Reference Citation Analysis (0)] |
| 11. | Fuller JA, Stanton JM, Fisher GG, Spitzmuller C, Russell SS, Smith PC. A lengthy look at the daily grind: time series analysis of events, mood, stress, and satisfaction. J Appl Psychol. 2003;88:1019-1033. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 116] [Cited by in RCA: 73] [Article Influence: 3.5] [Reference Citation Analysis (0)] |
| 12. | Chan YH. Biostatistics 201: linear regression analysis. Singapore Med J. 2004;45:55-61. [PubMed] |
| 13. | Dinc E. Linear regression analysis and its application to the multivariate spectral calibrations for the multiresolution of a ternary mixture of caffeine, paracetamol and metamizol in tablets. J Pharm Biomed Anal. 2003;33:605-615. [RCA] [DOI] [Full Text] [Cited by in Crossref: 18] [Cited by in RCA: 17] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 14. | Chen JJ. Communicating complex information: the interpretation of statistical interaction in multiple logistic regression analysis. Am J Public Health. 2003;93:1376-1377; author reply 1377. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 20] [Cited by in RCA: 20] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 15. | Mohamed EI, Linder R, Perriello G, Di Daniele N, Pöppl SJ, De Lorenzo A. Predicting Type 2 diabetes using an electronic nose-based artificial neural network analysis. Diabetes Nutr Metab. 2002;15:215-221. [PubMed] |
| 16. | Becerikli Y, Konar AF, Samad T. Intelligent optimal control with dynamic neural networks. Neural Netw. 2003;16:251-259. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 65] [Cited by in RCA: 64] [Article Influence: 2.9] [Reference Citation Analysis (0)] |
| 17. | Kao JJ, Huang SS. Forecasts using neural network versus Box-Jenkins methodology for ambient air quality monitoring data. J Air Waste Manag Assoc. 2000;50:219-226. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 22] [Cited by in RCA: 2] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 18. | Dassen WR, Mulleneers RG, Den Dulk K, Smeets JR, Cruz F, Penn OC, Wellens HJ. An artificial neural network to localize atrioventricular accessory pathways in patients suffering from the Wolff-Parkinson-White syndrome. Pacing Clin Electrophysiol. 1990;13:1792-1796. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 19] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 19. | Cimander C, Bachinger T, Mandenius CF. Integration of distributed multi-analyzer monitoring and control in bioprocessing based on a real-time expert system. J Biotechnol. 2003;103:237-248. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 36] [Cited by in RCA: 36] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 20. | Augusteijn MF, Shaw KA. Constructing a query-able radial basis function artificial neural network. Int J Neural Syst. 2002;12:159-175. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1] [Cited by in RCA: 1] [Article Influence: 0.0] [Reference Citation Analysis (0)] |
| 21. | Castellaro C, Favaro G, Castellaro A, Casagrande A, Castellaro S, Puthenparampil DV, Salimbeni CF. An artificial intelligence approach to classify and analyse EEG traces. Neurophysiol Clin. 2002;32:193-214. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 21] [Cited by in RCA: 22] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 22. | Yen GG, Meesad P. Constructing a fuzzy rule-based system using the ILFN network and Genetic Algorithm. Int J Neural Syst. 2001;11:427-443. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 5] [Cited by in RCA: 5] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 23. | Ignat'ev NA, Adilova FT, Matlatipov GR, Chernysh PP. Knowledge discovering from clinical data based on classification tasks solving. Stud Health Technol Inform. 2001;84:1354-1358. [PubMed] |
| 24. | Traeger M, Eberhart A, Geldner G, Morin AM, Putzke C, Wulf H, Eberhart LH. [Artificial neural networks. Theory and applications in anesthesia, intensive care and emergency medicine]. Anaesthesist. 2003;52:1055-1061. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 13] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 25. | Catto JW, Linkens DA, Abbod MF, Chen M, Burton JL, Feeley KM, Hamdy FC. Artificial intelligence in predicting bladder cancer outcome: a comparison of neuro-fuzzy modeling and artificial neural networks. Clin Cancer Res. 2003;9:4172-4177. [RCA] [DOI] [Full Text] [Cited by in Crossref: 8] [Cited by in RCA: 8] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 26. | Ritchie MD, White BC, Parker JS, Hahn LW, Moore JH. Optimization of neural network architecture using genetic programming improves detection and modeling of gene-gene interactions in studies of human diseases. BMC Bioinformatics. 2003;4:28. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 157] [Cited by in RCA: 115] [Article Influence: 5.2] [Reference Citation Analysis (0)] |
| 27. | Hajmeer MN, Basheer IA. A hybrid Bayesian-neural network approach for probabilistic modeling of bacterial growth/no-growth interface. Int J Food Microbiol. 2003;82:233-243. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 36] [Cited by in RCA: 36] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 28. | Casillas AM, Clyman SG, Fan YV, Stevens RH. Exploring Alternative Models of Complex Patient Management with Artificial Neural Networks. Adv Health Sci Educ Theory Pract. 2000;5:23-41. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 8] [Cited by in RCA: 9] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 29. | Traeger M, Eberhart A, Geldner G, Morin AM, Putzke C, Wulf H, Eberhart LH. [Prediction of postoperative nausea and vomiting using an artificial neural network]. Anaesthesist. 2003;52:1132-1138. [PubMed] |
| 30. | Jerez-Aragonés JM, Gómez-Ruiz JA, Ramos-Jiménez G, Muñoz-Pérez J, Alba-Conejo E. A combined neural network and decision trees model for prognosis of breast cancer relapse. Artif Intell Med. 2003;27:45-63. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 146] [Cited by in RCA: 83] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 31. | Tambouratzis T, Gazela M. The accurate estimation of meteorological profiles employing ANNs. Int J Neural Syst. 2002;12:319-337. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 2] [Cited by in RCA: 2] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 32. | Ma L, Khorasani K. New training strategies for constructive neural networks with application to regression problems. Neural Netw. 2004;17:589-609. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 82] [Cited by in RCA: 80] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 33. | Callan DE, Kent RD, Guenther FH, Vorperian HK. An auditory-feedback-based neural network model of speech production that is robust to developmental changes in the size and shape of the articulatory system. J Speech Lang Hear Res. 2000;43:721-736. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 92] [Cited by in RCA: 82] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 34. | Sasagawa F, Tajima K. Prediction of protein secondary structures by a neural network. Comput Appl Biosci. 1993;9:147-152. [PubMed] |
| 35. | Goodwin N, Sunderland A. Intensive, time-series measurement of upper limb recovery in the subacute phase following stroke. Clin Rehabil. 2003;17:69-82. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 17] [Cited by in RCA: 16] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 36. | Haydon DT, Shaw DJ, Cattadori IM, Hudson PJ, Thirgood SJ. Analysing noisy time-series: describing regional variation in the cyclic dynamics of red grouse. Proc Biol Sci. 2002;269:1609-1617. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 38] [Cited by in RCA: 33] [Article Influence: 1.4] [Reference Citation Analysis (0)] |