Published online Nov 28, 2005. doi: 10.3748/wjg.v11.i44.6995
Revised: April 15, 2005
Accepted: April 18, 2005
Published online: November 28, 2005
AIM: To introduce a computer-aided morphometric method for quantifying the necro-inflammatory phase in liver biopsy specimens using fractal geometry and Delaunay’s triangulation.
METHODS: Two-micrometer thick biopsy sections taken from 78 chronic hepatitis C virus-infected patients were immunohistochemically treated to identify the inflammatory cells. An automatic computer-aided image analysis system was used to define the inflammatory cell network defined on the basis of Delaunay’s triangulation, and the inflammatory cells were geometrically classified as forming a cluster (an aggregation of a minimum of three cells) or as being irregularly distributed within the tissue. The phase of inflammatory activity was estimated using Hurst’s exponent.
RESULTS: The proposed automatic method was rapid and objective. It could not only provide rigorous results expressed by scalar numbers, but also allow the state of the whole organ to be represented by Hurst’s exponent with an error of no more than 12%.
CONCLUSION: The availability of rigorous metrical measures and the reasonable representativeness of the status of the organ as a whole raise the question as to whether the indication for hepatic biopsy should be revised by establishing clear rules concerning the contraindications suggested by its invasiveness and subjective interpretation.
- Citation: Dioguardi N, Franceschini B, Russo C, Grizzi F. Computer-aided morphometry of liver inflammation in needle biopsies. World J Gastroenterol 2005; 11(44): 6995-7000
- URL: https://www.wjgnet.com/1007-9327/full/v11/i44/6995.htm
- DOI: https://dx.doi.org/10.3748/wjg.v11.i44.6995
The antiviral treatment of chronic hepatitis C is expensive, efficacious in only 50% of cases, and has sometimes major undesired effects. The criteria for selecting the patients to treat are therefore a central problem and its solution is sought by evaluating the inflammatory lesions (grading) and fibrosis (staging) histologically observed in bioptic specimens.
A single bioptic sample is still the most effective means of obtaining the greatest amount of information for formulating a diagnosis of chronic hepatitis, excluding other diseases, hypothesizing the prognosis, and defining therapeutic indications[1-4]. However, taking a bioptic sample is expensive, carries a certain risk, and the results are not reliable insofar as they do not express real measures, but only semi-quantitative categories of severity, and its evaluation entirely depends on the subjective skill and experience of the pathologist[5-9]. It therefore follows that such semi-quantitative data cannot be used for statistical purposes[10,11].
The recently proposed alternative methods of estimating hepatic tissue inflammation by measuring the blood levels of molecules associated with the evolution of liver inflammation (including the extremely and widely used measurement of transaminase levels) have not shown any sure correspondence with actual tissue status[12-16].
It is therefore necessary to develop more rigorous and objective morphometric methods capable of providing scalars for the metrical quantification of inflammation structures within a liver biopsy sample. We have herein described the first results of our metrical measurements of the fractal spaces covered by necro-inflammatory lesions observed in the biopsies of consecutive chronic hepatitis C patients, and obtained by means of a totally computerized analysis that excludes any subjective influence.
The phase of inflammatory activity in the examined samples has been estimated using Hurst’s exponent (H). H was first excogitated in the middle of the last century in order to study the local variations in water flow in the branches of the Nile delta during the construction of the Aswan dam[17]. Further refined in 1965 and 1969, it can now be drawn from the fractal dimension (D)[18,19]. As it can describe even subtle quantitative differences in the smoothness of the configurations of natural objects with fractal properties, we used it to describe the phase of the inflammatory process on the basis of the fractal space occupied by inflammatory cells. In our case, a high H value indicates a small number of inflammatory cells within the tissue (i.e. the natural state), and a low value indicates the presence of many inflammatory cells (i.e. severe inflammatory states). H can be considered as a quantitative descriptor of the configuration pattern expressing the phase of the inflammatory process, and thus gives inflammatory cell density, the significance of a physical variable.
The study was conducted in accordance with the guidelines of the Ethics Committee of Istituto Clinico Humanitas, Rozzano, Milan, Italy.
The 72 liver specimens (>10 mm long) came from 43 male and 29 female chronic hepatitis C patients (mean age 50.3±14 years; range 25-77 years) admitted to our Hepato-gastroenterology Unit.
Two consecutive 2-µm-thick sections were cut from the formalin-fixed and paraffin-embedded specimens. One was subsequently stained with hematoxylin-eosin (HE) solution, and the other was used for immunohistochemistry. HE stained sections were graded by two hepato-pathologists using a semi-quantitative scoring system.
In order to classify the inflammatory cells, the histological sections were treated with primary antibodies raised against human leukocyte common antigen (LCA, monoclonal mouse anti-LCA) for 1 h at room temperature, 1 mg/mL mouse IgG1 (Dako, Milan, Italy) was used as a negative control.
In order to distinguish settled macrophagic mesenchymal Kupffer cells from recruited inflammatory T cells, a further section was immersed in an antigen retrieval bath (Dako, Milan, Italy) for 30 min at 98 °C in 1 mmol/L of a freshly made EDTA solution. The inflammatory T cells were classified using primary antibodies raised against human CD3 (Dako, Milan, Italy), and the Kupffer cells by treatment with primary antibodies raised against human CD68 (Dako, Milan, Italy) at room temperature, or with 1 mg/mL mouse IgG1 (Dako, Milan, Italy) as a negative control.
The sections were then incubated with the DAKO Envision Doublestain System (Dako, Milan, Italy). Fast red was used as a chromogen to yield the red reaction products for CD68, and 3,3’-diaminobenzidine tetrahydrochloride (DAB, Sigma Ltd, MO, USA) to yield the brown reaction products for LCA and CD3.
The nuclei were lightly counterstained with Harris’s hematoxylin solution (Medite, Bergamo, Italy).
The histological sections were digitized using an image analysis system consisting of a Leica DMLA microscope (Leica, Italy) equipped with an x-y translator table, a digital camera (Leica DC200, Leica, Italy), and an Intel dual Pentium IV, 660 MHz computer with incorporated ad hoc constructed image analysis software[20].
The computer program automatically selected the surface covered by the whole LCA-immunopositive inflammatory system. In this paper, the term true area indicates the surface of the liver tissue section without unfilled natural holes, vascular and biliary cavities, sinusoidal spaces or artificial spaces due to the needle excision and histological manipulations[20]. All the measurements were made at an objective magnification of ×20.
This was obtained using the general relationship:
H=E+1-D (1)
where E indicates the Euclidean topological dimension and D the fractal dimension of the surface covered by the whole LCA-immunopositive inflammatory system.
D was automatically estimated using the box-counting method and the formula:
Math 1
where DB is the box-counting fractal dimension of the object, ε the side length of the box, and N(ε) the smallest number of boxes of side ε required to cover the surface of the object completely, i.e. the whole LCA-immunopositive inflammatory system. As the zero limit cannot be applied to biological objects, the dimensions were calculated as D=d, where d is the slope of the graph of log [N(ε)] against log 1/ε. The log-log graphs were plotted and the linear segments were identified using least squares regression. Their gradients were calculated using an iterative resistant line method[20-28].
On the basis of the H value, two categories were considered. The first included all the samples characterized by 0.5<H<1.0, and the second included all the samples verifying the relationship 0<H<0.5.
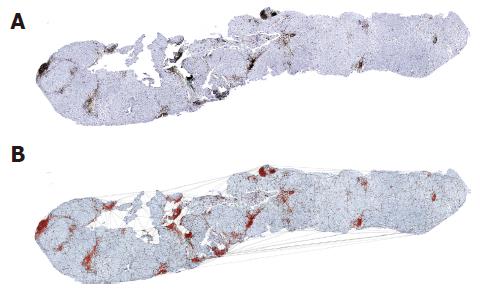
The pictures indicating chronic liver inflammation appeared as portal, periportal, and perilobular aggregations of lymphocytes, plasma cells, and monocytes/macrophages (Figure 1). The extent of intralobular focal necro-inflammation varied with the severity of the disease, with confluent necrosis expressing its most severe clinical exacerbation[29-33].
These cell conglomerates arose when the viral etiological agent shaped critical points in the liver tissue consistent with hepatocyte necrosis. Each critical point acted as an attractor of the inflammatory cells naturally present within the liver tissue and recruited lymphocytes, plasma cells and other white blood cells. The trajectories of the inflammatory cells would die inside the attraction basin created by the necro-inflammatory process, where the motion of the recruited cells came to an end, and they formed a cluster marking the metrical space covered by the inflammation basin. The cell density of the cluster was transient and depended on the evolution of the inflammation connected to necrosis healing.
As the cells of a cluster were not settled in tasseled forms, they were not bounded by a distinguishable contour. This meant that, in order to measure the fractal spaces they covered, the canonical step was to fix their bounds. To this end, we used a triangulation method based on the principles of Delaunay’s tessellation[34-37], which can be very efficiently adapted to cluster geometry and involves the metrical measurement of the distances between the cells belonging to the whole inflammatory system.
Each inflammatory cell on the surface of the histological specimen was considered as a node of a continuous framework covering the entire section characterized by very irregular triangular windows in which any two triangles have one common side (Figure 1).
The border of the cluster (Figure 2) was arbitrarily fixed at the level of the continuous line formed by the set of the most external triangle sides with a length of ≤20 µm, corresponding to about twice the mean diameter of a lymphocyte (7-12 µm)[38]. All the points within this border were considered as belonging to the subset of cluster-resident cells, and those connected by longer segments as belonging to the non-clustered subset of inflammatory cells.
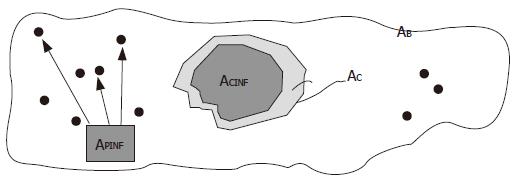
The dynamics of the necro-inflammation shaping a cluster generate metrical spaces covered by two overlapping components. One belonged to the entire attraction basin of hepatocyte necrosis bounded by the cluster contour drawn by the triangulation, the other belonged to the sum of the surfaces of the inflammatory cells residing within the attraction (necro-inflammation) basin. The outline of the true area of the biopsy sample was indicated by the symbol AB, the area of the triangulation-defined cluster (necrosis attraction zone) was indicated by the symbol AC, and the sum of the areas of cluster-resident inflammatory cells was indicated by the symbol ACINF (Figure 3). The dispersed cells were indicated by the symbol APINF, and their areas added to the area of resident inflammatory cells provided the area covered by the inflammation system as a whole, which was indicated by the symbol ATINF
The physical parameters of inflammation were taken from analyses of the clusters consisting of at least three inflammatory cells. Smaller aggregates were considered as randomly united cells.
In the two dimensions of a histological section, we obtained the following physical parameters relating to the state of inflammation: (1) cluster extension: the area of the necro-inflammation basins identified by means of Delaunay’s triangulation; (2) the area covered by the inflammatory cells resident within the cluster perimeter: i.e. the intracluster mass of inflammatory cells; (3) the whole area occupied by all the inflammatory parenchymal cells not residing inside the clusters; (4) the AC/ACINF ratio; (5) the extent of inflammatory tissue as a whole (ACINF+APINF); (6) the discrimination of inflammatory T cells from Kupffer cells; (7) Hurst’s exponent in order to evaluate the spatial heterogeneity of the chronic inflammatory process, i.e. the phase of the inflammatory process.
All the data were expressed as mean±SD.
The area of the necro-inflammation basins obtained by Delaunay’s triangulation ranged from 0.010% to 33.74% (mean 5.22±6.5%) of the area of the histological section. This area was a perceptible and measurable marker of the necrosis subtending each cluster. The sum of these areas could express the overall extension of the necrotic process in the evaluated section.
This area ranged from 0.021% to 15.36% (mean 2.22±2.9%) of the area of the histological section. As it represented effective inflammatory activity, its measure indicated the inflammatory potential of the set of clusters identified in the biopsy section.
The area covered by the whole set of LCA-immunopositive inflammatory cells lying outside the clusters recognized in the histological sections ranged from 0.024% to 3.93% (mean 0.91±0.83%).
This parameter, which expresses the density of the inflammatory cells lying within the clusters, ranged from 0.34 to 3.28 (mean 0.56±0.35).
This area was drawn from the sum of the clustered and dispersed inflammatory cells immunopositive for LCA, and ranged from 0.045% to 18.58% (mean 3.13±3.30%).
The whole LCA-immunopositive inflammatory area was shared by recruited blood cells (lymphocytes, monocytes, plasma cells, mast cells) and settled macrophagic Kupffer cells (Figure 4). The different range of the areas of Kupffer cells suggested that the number of Kupffer cells potentially capable of being activated might explain the distinction between fast and slow fibrosis. It is worth mentioning that this preliminary study found a high percentage of macrophages among the dispersed cells and a very low percentage in the clusters, which mainly consisted of lymphocytes and other recruited blood inflammation cells (Figure 4).
This was evaluated using Hurst’s exponent, the values of which range from 0 to 1 and indicate the actual phase of the inflammatory process. H coefficients of >0.5 were considered as belonging to tendentially less severe inflammatory pictures, and those of <0.5 as belonging to more severe pictures. The mean H value of all the cases was 0.67±0.14 (range 0.36-1).
Given a hierarchy of logical concepts going from the purely qualitative or classificatory, to the semi-quantitative or ordering, and finally to the entirely quantitative or metrical (i.e. scientific variables), it is not a prejudice to consider that the maturity of a discipline is reflected by the number of quantitative concepts it adopts.
From this viewpoint, the phasing out of the clinical use of qualitative and semi-quantitative methods when evaluating the extension of chronic inflammatory lesions can be correlated with the maturity of hepatological disciplines. In this study, we used measurement theory, which forms the basis of our concrete knowledge of the real world and discriminates the specificity of its interrelationships, to construct a method of evaluating the different pictures of chronic liver inflammation.
Studying the measurement of inflammation (or the intensity of a process) obliged us to think in different terms from those that we were used to. In order to express new facts in intelligible terms, the confusion generated by the vague and emotive semi-quantitative definitions dictated by an observer’s skill must be removed from every conceptual structure.
The method adopted by us is highly objective insofar as it is entirely computerized. Its foundations lie in the theory of measurement, a basic point of reference for all conceptual structures organizing knowledge[39].
The liver tissue lesions related to the inflammatory process at any given time caused variations in the concentrations of some specific blood molecules. These have been grouped and proposed as disease indices despite the fact that their concentrations depend not only on their production, but also on the rate of their metabolism in the bloodstream, thus depriving them of much of their significance as a quantitative index of the hepatic structure producing them. The changes in the concentrations of these blood indices over time can be described by the general equation:
dxi/dt = fi (x1, x2,…, xn) (3)
where xi denotes the blood concentration of the molecular species used, t is time, and the functions fi are determined by the specific reactions of each xi with the environmental factors in the bloodstream that affect their mean life (many of which are unknown).
This makes these blood molecules independent variables that are incapable of expressing the state conditions of hepatic tissue even when the most sophisticated statistical methods are used. Similar conclusions can be made concerning the figured elements of blood (granulocytes, red cells, and platelets), and the characteristics of independent variables can also be found in the case of hepatofuge circulations (esophageal, gastric, hemorrhoidal, and umbilical varices). It therefore follows that the only variables describing the state of a chronic necro-inflammatory hepatic tissue lesion are those obtained by measuring their characteristics in the tissue in which they occur.
Since all theoretical hepatologists freely admit that the forms of chronic viral inflammation are so numerous and that they elude a complete verbal description, metrical measurements estimating the size of the true area covered by inflammatory cells and the density of the cells occupying it are the most real means of defining the stage of the process.
In practical terms, measuring chronic hepatitis B and C virus-related inflammation on the basis of a histological section of liver tissue is a problem of estimating the density of the points aggregated in clusters and those isolated in the interstitium of the hepatic parenchyma. As the points of the former (lymphocytes, monocytes, plasma cells) and the latter (which also include Kupffer cells) have the same mesenchymal nature and a similar capacity of activation during disease, it can be reasonably presumed that the degree of activity of the chronic viral process can be estimated by measuring the metrical spaces occupied by these cells and their density within them.
Whatever the method used, it is always difficult to determine the density of the punctiform particles representing the recruited inflammatory blood cells in a cluster because it depends on what is assumed to be the boundary of these basic elements of the chronic hepatitis virus-related process of liver tissue inflammation. After repeated tests (not described here), we decided to use cell sequences characterized by intercellular distances of ≤20 µm. Although this resolved our case, it certainly did not provide definitive solutions.
One basic question raised by our study is how much new knowledge of inflammation we have acquired after recognizing, measuring and classifying it. A first reply can be that we are able to acquire rigorous and repeatable metrical data concerning the anatomical (i.e. physical) state of the lesions induced by the etiological agent, which can be used as a reference point to give some significance to the hematological indices of disease whose uncertainty is always due to partially unknown factors. No other method of tissue or hematological analysis offers a result that is so near to reality.
Furthermore, using the same equation (4), we can now geometrically describe the morphometry of the histological picture offered by a liver biopsy. In this case, xi represents the observable (i.e. measurable) quantities indicating the phase of the dynamic state of the inflammatory lesions that directly mark the evolution of the disease, t is time, and the functions fi are determined by both viral and immune activity.
We included in xi the observable, directly perceivable and metrically quantifiable measures that can change the blood concentrations of the individual molecules indicative of chronic liver disease.
Tissue and hematological indices can both be seen as dynamic variables and written using the same formula, but the hematological indices described by equation (3) are completely different functions (fi) from those determining the dynamics of anatomical lesions. It therefore follows that blood indices cannot be used to validate the results of our method, and that the changes in hematological indices are due to the action of very different independent factors.
At this point, it may be wondered what qualitative differences distinguish our method from previous recognition/classification and evaluation procedures. The most immediate reply is the rigorousness of the results expressed by scalar numbers, but it should also be added that our method allows the state of the whole organ to be represented by Hurst’s exponent with an error of no more than 12% (manuscript in preparation).
The availability of rigorous metrical measures and the reasonable representativeness of the status of the organ as a whole raise the question as to whether the indication for hepatic biopsy should be reviewed by establishing clear rules in relation to the contraindications suggested by its invasiveness.
Science Editor Wang XL and Guo SY Language Editor Elsevier HK
| 1. | Kleiner DE. The liver biopsy in chronic hepatitis C: a view from the other side of the microscope. Semin Liver Dis. 2005;25:52-64. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 50] [Cited by in F6Publishing: 49] [Article Influence: 2.6] [Reference Citation Analysis (0)] |
| 2. | Desmet VJ. Liver tissue examination. J Hepatol. 2003;39 Suppl 1:S43-S49. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 25] [Cited by in F6Publishing: 25] [Article Influence: 1.3] [Reference Citation Analysis (0)] |
| 3. | Bravo AA, Sheth SG, Chopra S. Liver biopsy. N Engl J Med. 2001;344:495-500. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 1678] [Cited by in F6Publishing: 1647] [Article Influence: 71.6] [Reference Citation Analysis (0)] |
| 4. | Brunt EM. Liver biopsy interpretation for the gastroenterologist. Curr Gastroenterol Rep. 2000;2:27-32. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 19] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 5. | Brunt EM. Grading and staging the histopathological lesions of chronic hepatitis: the Knodell histology activity index and beyond. Hepatology. 2000;31:241-246. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 324] [Cited by in F6Publishing: 340] [Article Influence: 14.2] [Reference Citation Analysis (0)] |
| 6. | Hübscher SG. Histological grading and staging in chronic hepatitis: clinical applications and problems. J Hepatol. 1998;29:1015-1022. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 70] [Cited by in F6Publishing: 75] [Article Influence: 2.9] [Reference Citation Analysis (0)] |
| 7. | Scheuer PJ. Assessment of liver biopsies in chronic hepatitis: how is it best done? J Hepatol. 2003;38:240-242. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 13] [Cited by in F6Publishing: 13] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 8. | Rosenberg WM. Rating fibrosis progression in chronic liver diseases. J Hepatol. 2003;38:357-360. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 31] [Cited by in F6Publishing: 32] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 9. | Guido M, Rugge M. Liver biopsy sampling in chronic viral hepatitis. Semin Liver Dis. 2004;24:89-97. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 125] [Cited by in F6Publishing: 120] [Article Influence: 6.0] [Reference Citation Analysis (0)] |
| 10. | Lagging LM, Westin J, Svensson E, Aires N, Dhillon AP, Lindh M, Wejstål R, Norkrans G. Progression of fibrosis in untreated patients with hepatitis C virus infection. Liver. 2002;22:136-144. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 58] [Cited by in F6Publishing: 61] [Article Influence: 2.8] [Reference Citation Analysis (0)] |
| 11. | Svensson E. Ordinal invariant measures for individual and group changes in ordered categorical data. Stat Med. 1998;17:2923-2936. [PubMed] [DOI] [Cited in This Article: ] [Cited by in F6Publishing: 2] [Reference Citation Analysis (0)] |
| 12. | Poynard T, Imbert-Bismut F, Munteanu M, Messous D, Myers RP, Thabut D, Ratziu V, Mercadier A, Benhamou Y, Hainque B. Overview of the diagnostic value of biochemical markers of liver fibrosis (FibroTest, HCV FibroSure) and necrosis (ActiTest) in patients with chronic hepatitis C. Comp Hepatol. 2004;3:8. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 250] [Cited by in F6Publishing: 269] [Article Influence: 13.5] [Reference Citation Analysis (0)] |
| 13. | Silva IS, Ferraz ML, Perez RM, Lanzoni VP, Figueiredo VM, Silva AE. Role of gamma-glutamyl transferase activity in patients with chronic hepatitis C virus infection. J Gastroenterol Hepatol. 2004;19:314-318. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 50] [Cited by in F6Publishing: 45] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 14. | Myers RP, Tainturier MH, Ratziu V, Piton A, Thibault V, Imbert-Bismut F, Messous D, Charlotte F, Di Martino V, Benhamou Y. Prediction of liver histological lesions with biochemical markers in patients with chronic hepatitis B. J Hepatol. 2003;39:222-230. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 248] [Cited by in F6Publishing: 265] [Article Influence: 12.6] [Reference Citation Analysis (0)] |
| 15. | He QY, Lau GK, Zhou Y, Yuen ST, Lin MC, Kung HF, Chiu JF. Serum biomarkers of hepatitis B virus infected liver inflammation: a proteomic study. Proteomics. 2003;3:666-674. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 125] [Cited by in F6Publishing: 122] [Article Influence: 5.8] [Reference Citation Analysis (0)] |
| 16. | Lichtinghagen R, Bahr MJ. Noninvasive diagnosis of fibrosis in chronic liver disease. Expert Rev Mol Diagn. 2004;4:715-726. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 32] [Cited by in F6Publishing: 33] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 17. | Hurst HE. Long-term storage capacity of reservoirs. Trans Amer Soc Civ Eng. 1951;116:770-808. [Cited in This Article: ] |
| 18. | Hurst HE, Black RP, Simaiki YM. Long-term storage: an experimental study. London: Constable 1965; . [Cited in This Article: ] |
| 19. | Bassingthwaighte JB, Raymond GM. Evaluation of the dispersional analysis method for fractal time series. Ann Biomed Eng. 1995;23:491-505. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 108] [Cited by in F6Publishing: 67] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 20. | Bassingthwaighte JB, Liebovitch LS. West BJ: Fractal physiology. New York: Oxford University Press. 1994;. [DOI] [Cited in This Article: ] |
| 21. | Dioguardi N, Franceschini B, Aletti G, Russo C, Grizzi F. Fractal dimension rectified meter for quantification of liver fibrosis and other irregular microscopic objects. Anal Quant Cytol Histol. 2003;25:312-320. [PubMed] [Cited in This Article: ] |
| 22. | Dioguardi N, Grizzi F, Bossi P, Roncalli M. Fractal and spectral dimension analysis of liver fibrosis in needle biopsy specimens. Anal Quant Cytol Histol. 1999;21:262-266. [PubMed] [Cited in This Article: ] |
| 23. | Hastings HM, Sugihara G. Fractals. A User's Guide for the Natural Sciences. Oxford: Oxford Science Publications. 1993;. [Cited in This Article: ] |
| 24. | Nonnenmacher TF, Baumann G, Barth A, Losa GA. Digital image analysis of self-similar cell profiles. Int J Biomed Comput. 1994;37:131-138. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 29] [Cited by in F6Publishing: 31] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 25. | Losa GA, Nonnenmacher TF. Self-similarity and fractal irregularity in pathologic tissues. Mod Pathol. 1996;9:174-182. [PubMed] [Cited in This Article: ] |
| 26. | Cross SS. Fractals in pathology. J Pathol. 1997;182:1-8. [PubMed] [DOI] [Cited in This Article: ] [Cited by in F6Publishing: 2] [Reference Citation Analysis (0)] |
| 27. | Grizzi F, Dioguardi N. A fractal scoring system for quantifying active collagen synthesis during chronic liver disease. Int J Chaos Theo Appl. 1999;4:39-44. [Cited in This Article: ] |
| 28. | Dioguardi N, Grizzi F. Fractal dimension exponent for quantitative evaluation of liver collagen in bioptic specimens. In "Mathematics and Biosciences in interaction", Basel, Boston, Berlin: Birkhauser Press 2001; 113-120. [Cited in This Article: ] |
| 29. | Ishak KG. Pathologic features of chronic hepatitis. A review and update. Am J Clin Pathol. 2000;113:40-55. [PubMed] [Cited in This Article: ] |
| 30. | Nathan C. Points of control in inflammation. Nature. 2002;420:846-852. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 1820] [Cited by in F6Publishing: 1762] [Article Influence: 80.1] [Reference Citation Analysis (0)] |
| 31. | Baptista A, Bianchi L, De Groote J, Desmet VJ, Ishak KG, Korb G, MacSween RN, Popper H, Poulsen H, Scheuer PJ. The diagnostic significance of periportal hepatic necrosis and inflammation. Histopathology. 1988;12:569-579. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 20] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 32. | Ishak K, Baptista A, Bianchi L, Callea F, De Groote J, Gudat F, Denk H, Desmet V, Korb G, MacSween RN. Histological grading and staging of chronic hepatitis. J Hepatol. 1995;22:696-699. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 3521] [Cited by in F6Publishing: 3596] [Article Influence: 124.0] [Reference Citation Analysis (1)] |
| 33. | Villari D, Raimondo G, Brancatelli S, Longo G, Rodinò G, Smedile V. Histological features in liver biopsy specimens of patients with acute reactivation of chronic type B hepatitis. Histopathology. 1991;18:73-77. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 8] [Cited by in F6Publishing: 8] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 34. | Wallet F, Dussert C. Multifactorial comparative study of spatial point pattern analysis methods. J Theor Biol. 1997;187:437-447. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 20] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 35. | Fortune S. A Sweepline Algorithm for Voronoi Diagrams. Algorithmica. 1987;2:153-174 DOI : 10.1007/BF01840357. [Cited in This Article: ] |
| 36. | Fitzsimons CJ, Nikjoo H, Bolton CE, Goodhead DT. A novel algorithm for tracing the interaction of a track with molecular targets--use of Delaunay triangulation. Math Biosci. 1998;154:103-115. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 3] [Cited by in F6Publishing: 3] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 37. | Bostick D, Vaisman II. A new topological method to measure protein structure similarity. Biochem Biophys Res Commun. 2003;304:320-325. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 23] [Cited by in F6Publishing: 24] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 38. | Weiler-Normann C, Rehermann B. The liver as an immunological organ. J Gastroent Hepatol. 2004;19:S279-S283. [Cited in This Article: ] |
| 39. | Rosen R. Fundamentals of measurements and representation of natural systems. Amsterdam: North-Holland 1978; . [Cited in This Article: ] |