Revised: February 17, 2012
Accepted: February 21, 2012
Published online: February 26, 2012
Eight dissolution models of calcium apatites (both fluorapatite and hydroxyapatite) in acids were drawn from the published literature, analyzed and discussed. Major limitations and drawbacks of the models were conversed in details. The models were shown to deal with different aspects of apatite dissolution phenomenon and none of them was able to describe the dissolution process in general. Therefore, an attempt to combine the findings obtained by different researchers was performed which resulted in creation of the general description of apatite dissolution in acids. For this purpose, eight dissolution models were assumed to complement each other and provide the correct description of the specific aspects of apatite dissolution. The general description considers all possible dissolution stages involved and points out to some missing and unclear phenomena to be experimentally studied and verified in future. This creates a new methodological approach to investigate reaction mechanisms based on sets of affine data, obtained by various research groups under dissimilar experimental conditions.
- Citation: Dorozhkin SV. Dissolution mechanism of calcium apatites in acids: A review of literature. World J Methodol 2012; 2(1): 1-17
- URL: https://www.wjgnet.com/2222-0682/full/v2/i1/1.htm
- DOI: https://dx.doi.org/10.5662/wjm.v2.i1.1
Calcium apatites [hydroxyapatite (HA): Ca10(PO4)6(OH)2 and fluorapatite (FA): Ca10(PO4)6F2] appear to be of a special interest to the mankind, because natural apatites are the main source of inorganic phosphorus in nature[1], while calcified tissues (bones and teeth) of mammals consist of ion-substituted calcium apatites of biological origin[2-4]. Therefore, HA and FA are widely used in various aspects of human being, starting from the major source of phosphorus-containing fertilizer production and ending with various biomedical applications, for example, using as artificial bone grafts. The latter resulted in a great number of research papers published on calcium apatites and related calcium orthophosphates[5-7]. Since the chemical nature of natural phosphate ores and the inorganic phase of bones and teeth is almost the same, such different processes as fertilizer production, dental caries, osteoporosis, as well as both in vitro and in vivo biodegradation of artificial bone grafts might be simulated by dissolution of chemically pure calcium apatites (HA and FA) in acids. Therefore, establishing of the true dissolution mechanism of calcium apatites in acids appears to be of the paramount importance for our species.
In chemistry, a reaction mechanism is the step by step sequence of elementary reactions by which the overall chemical change occurs[8]. Regarding the dissolution process of calcium apatites in acids, eight models have been already proposed to explain the processes involved. These models already provided the important information about the factors associated with solution (pH, composition, saturation and hydrodynamics), bulk solid (chemical composition, solubility, particle sizes) and surface (defects, adsorbed ions, “history”, phase transformation) of the apatite crystals. These findings cannot be underestimated because they have already made a significant impact on understanding of the medical aspects of both dental caries and osteoporosis, as well as they created the necessary fundamentals for fertilizer production industry. Nevertheless, there are still a lot of elements missing in the overall explanation for the processes involved.
To clarify possible directions of further investigations on apatite dissolution, a critical analysis of currently available models has been made in this review followed by an attempt to combine the data available into a general dissolution mechanism. This creates a new methodological approach to investigate reaction mechanisms based on sets of affine data, obtained by various research groups under dissimilar experimental conditions.
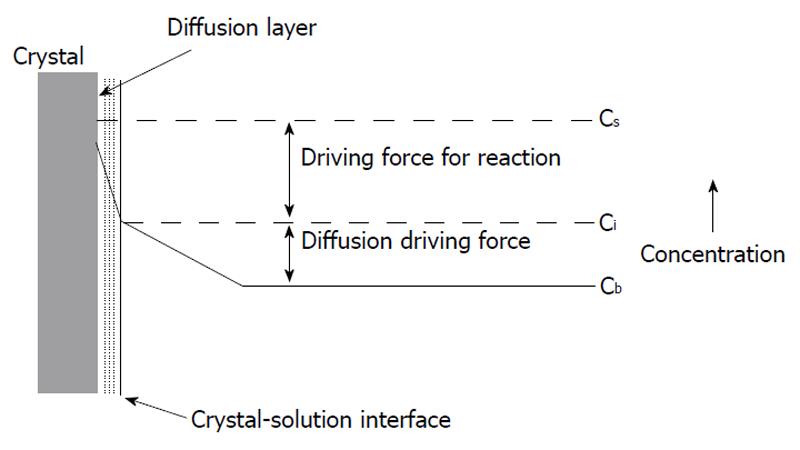
A diffusion (or transport) and a kinetically (or surface) controlled[9-30] dissolution models, as well as the two-site model[15,31-33], are devoted to comparison of transport rates of chemical reagents (H+ and anions of acid) from bulk solution to the surface of apatite crystals and those of products (Ca2+, F- and orthophosphate anions) obtained backwards with the kinetics of chemical interactions on the crystal surface. According to the diffusion-controlled and two-site models, a transport of either the chemical reagents and/or the products of chemical reactions mainly determine the overall dissolution rate, whereas the kinetically controlled model emphasizes chemical transformations on the surface as the limiting factor (Figure 1)[34]. An important consequence of the two types of rate-controlling mechanism is that the solution immediately next to the crystal surface is undersaturated with respect to apatite in the surface controlled process and this solution is saturated in the diffusion-controlled process[35]. Both models usually operate with a so-called “driving force” which means either a concentration gradient within the Nernst diffusion layer (the diffusion controlled model) or a gradient of ionic chemical potentials between the apatite crystal surface and bulk solution (the kinetically controlled model).
To investigate whether a dissolution process follows either of these models, one should study the influence of hydrodynamics, concentration of reagents, ionic strength, solution undersaturation, pH, temperature, crystal dimensions and the presence of chemical modifiers on the dissolution kinetics. A rotary disk[10,13,14], constant composition[9,16,18,19,20,36-38] or dual constant composition[22,38,39] techniques are used for experimental investigations. The results obtained are usually plotted as an uptake of H+ ions (e.g., as a titrant volume added) and/or a release of calcium, orthophosphate and fluoride ions versus the dissolution time. Afterwards, calculations of the numeric values for activation energy, rate constants, effective reaction order, diffusion layer thickness, characteristic adsorption impedance, diffusive jump distance, etc., are performed[9-33,36-40]. The conclusion on whether a dissolution process is kinetically or diffusion controlled is made based on the numeric values calculated. For example, when analysis of the rate data gave a numeric value of the effective reaction order n = 6, a surface controlled dissolution mechanism was suggested[22].
Basic thermodynamic principles predict that dissolution rates should increase with increasing driving force or chemical potential; however, the experimental studies show that this dependence is complex. Namely, dissolution of apatite in some cases was found to be diffusion controlled[19,20,23,25], in some other cases - kinetically controlled[21,22] and even intermediate (i.e., both kinetically and diffusion controlled) in still other cases[14]. Furthermore, the dissolution process might be composed of two stages: the first one was found to be both surface and diffusion controlled, while the second one was an exactly diffusion-controlled dissolution[24]. Therefore, the results obtained for these models are valid within the experimental conditions studied only; no extrapolation can be made outside the ranges studied. For example, after, say, an agitation decreasing or temperature increasing, an initially kinetically controlled dissolution might be controlled by diffusion[30].
Furthermore, in some cases, dissolution curves (a titrant volume against time) reach plateaus prior to complete dissolution of HA, thus indicating a creation of metastable states in which the reaction is effectively terminated even though apatite crystals remain in contact with the undersaturated solutions[41-53]. There is an opinion[54] that this effect resulted from a false solubility product value for HA. Thus, a high sensitivity to the experimental conditions appears to be the main drawback of these models.
The surface dissolution may be described by three different models shown schematically in Figure 2. As may be seen in Figure 2A it is possible to start dissolution from one center from which originates the units detachment leading to step disintegration. This is a mononuclear dissolution. It is also possible that detachment takes place simultaneously from multiple centers (Figure 2B and C) which may be developed in one or more steps on the crystal surface. This is a polynuclear dissolution. Alternatively, it has been suggested that the crystal units’ detachment takes place along spirals originating from an active site on the crystal surface following an Archimedean spiral (Figure 2D). The unit detachment along the spirals takes place at constant velocity[34].
A polynuclear model[55-64] was created from the study on apatite dissolution and growth kinetics under the constant composition conditions. Polydispersed samples of apatite were put into a stirred undersaturated (for dissolution experiments) or supersaturated (for those on crystal growth) solutions and the solution pH and amount of chemicals added (an acid for the dissolution experiments and a base for those on crystal growth) were permanently recorded as functions of time. The results obtained were plotted versus either undersaturation or supersaturation values: straight lines were obtained in the specific logarithmic coordinates typical for this model[65]. According to this model, dissolution nuclei, i.e., collections of vacant sites for Ca2+, PO43- and OH- ions, are formed on the crystal surface of apatite and spread over the surface with a definite lateral rate[56].
In polynuclear model, the nucleation rate is assumed as a function of the mean ion activity. A lateral growth rate of the nuclei is assumed proportional to the difference between the total concentration of calcium ions in the saturated solution and in a solution, while the rate constant is related to the frequency for calcium ions to make a diffusion jump into a kink and, simultaneously, partly dehydrate[62,63]. Investigations on apatite dissolution and crystal growth using atomic force microscopy revealed that the rate-determining step was not the diffusion but two-dimensional surface nucleation[66,67]. These observations provided a valuable support for the polynuclear model.
The experimental data on dissolution and growth rates versus undersaturation (S < 1) and supersaturation (S > 1) values, respectively, were obtained. Numeric values of surface tension (40 mJ/m2 for apatite dissolution and 100 mJ/m2 for apatite growth[62,63]), ionic frequencies to enter or leave a kink (1.6 × 105/s[61]), the mean distance between kinks in a surface nucleus (approximately 3.07 Å[60]) and the critical nuclei for both HA[55-59,62,63] and FA[60,61] were calculated. Furthermore, within 5.0 < pH < 7.2 the dissolution kinetics was found to follow the polynuclear model, while that of growth appeared to follow the polynuclear model within 5.5 < pH < 6.5 and the combined mono-polynuclear model at pH = 5.0[60,61].
A new idea about hydroxide ions formation at the hydroxide sites of HA from water molecules trapped under the crystal surface appeared in the most recent papers of this series[62,63]. Probably, this might be a reason for the above changing in the growth model found for HA at pH = 5.0. To conclude, the polynuclear model seems to be better elaborated among others because it is valid for apatite dissolution within solution pH of 5.0-7.2, saturation degrees of 0.1 < S < 7, and Ca/P molar ratios of 0.1-20[63]. However, nothing has been published on a validity of this model in more acidic solutions.
A model with a self-inhibition layer formation describes a formation of a calcium-rich layer on the surface of apatite during dissolution[19,49-53]. This model was created from the results on dissolution kinetics of apatite powders in acidic buffers at solution pH within 3.7-6.9 (the constant composition technique was used). Following concentration of calcium and solution pH, the authors found that during the initial period (2-5 min) of dissolution release of calcium into the bulk solution was always less when compared with consumption of H+. When dissolution progressed, rates of calcium release permanently increased and hydrogen uptake decreased until the equivalence (consumption of two hydrogen resulted in release of one calcium) was reached, while the over-all rate of apatite dissolution permanently decreased[19,49-53]. Similar decreasing of apatite dissolution rates were obtained by other research groups[41-48,68].
According to this model, apatite is dissolved by ionic detachment of calcium and orthophosphate ions from the surface to a solution. When an initial portion of apatite has been dissolved, some amount of calcium cations (presumably, in connection with anionic counter ions) is returned from the solution and adsorbed back onto the surface of apatite. The latter results in formation of a semi-permeable ionic membrane consisting of a positively charged layer containing strongly adsorbed calcium ions, i.e., a calcium-rich layer is formed[19,49-53]. An indirect confirmation of the presence of a calcium-rich layer was obtained in the most recent paper of this series: for initial strong calcium undersaturation in solutions, attainment of a pseudo-steady state was very long[53]. The areas per adsorbed single PO43- and Ca2+ ions on HA surface at the point of zero charge (pH = 8.5) were estimated to be 33.1 ± 2.7 and 23.0 ± 2.1 Å2, respectively[69].
The authors of calcium-rich layer formation model suggested that the rate control of apatite dissolution was diffusion of calcium and/or orthophosphate ions through an interfacial surface layer formed during the initial portion of the dissolution process. This interface would be composed of the Nernst layer that would be adjacent to the calcium-rich layer. This last one would present low permeability making the dissolution process slower[19,49-53]. It is important to notice that these conclusions were made from the experiments on following calcium concentration and solution pH only; no measurements of the surface composition of apatites were performed.
As said by this model, ionic diffusion in solution results in a situation when ionic concentration near the surface layer of apatite is always higher than that in the bulk solution. Calcium concentration in the solution is also inhomogeneous: it decreases when the distance from the liquid/solid interfaces increases[19,49-53]. Therefore, the calcium-rich layer appears to be undoubtedly rich in calcium when compared with the bulk solution only. However, when compared with the bulk of solid apatite (Ca/P = 1.67) this layer appears to be calcium-rich (Ca/P > 1.67) when the counter anions An- (it is assumed, that apatite is dissolved in acid HnA, where An- is an anion) adsorbed from the solution are not taken into account. If the counter anions are calculated, a numeric value for Ca/(P+A) molar ratio on the surface will be around 1.67 in the case of zero charge on the surface.
On the other hand, ions of calcium might be adsorbed without the counter anions. This results in an electrical double layer formation on the solid/liquid interface with positive charge on apatite. Indeed, apatite is charged positively in acidic solutions. This effect was explained by adsorption of either protons only[70] or protons and calcium cations from the solution[71,72]. Certainly, the presence of a positive charge on apatite surface is in favor for the calcium-rich layer model but one should not forget that this charge might be caused by adsorption of protons only[70]. The dissolution rate reduction found by the authors and explained by the state of the interface (adsorption of calcium[53]) might also be explained by adsorption of some impurities those always present in the solution. Other explanations are also available[41-48]. Thus, unless the direct measurements of the calcium content on the surface are made, this model cannot be considered as experimentally proven.
A contradiction between the calcium-rich layer formation and polynuclear models can be outlined: sorption of calcium is likely to happen on the dissolution nuclei. In this case, some amount of the nuclei should disappear, as a result. No suggestions how to overcome this contradiction were found in the references.
To conclude this model, one should notice that due to the formation of a calcium-rich layer, a non-stoichiometric (incongruent) dissolution (see the next model) is suggested by default.
A congruent/incongruent (or stoichiometric/non-stoichiometric) dissolution[11,17,19,21,40,50,68,73-90] is based on the direct measurements of either the ionic concentrations in a solution[19,21,40,68,74-76,80,83,84,87,88,90] or the surface composition of apatites during dissolution[17,77,81]. According to the definitions, ions of a solid might be dissolved either simultaneously with the dissolution rates proportional to their molar concentrations (a congruent dissolution) or non-simultaneously with different values of the dissolution rates for each ion (an incongruent dissolution). The latter case always results in a situation when a surface layer with a chemical composition different from that of the bulk of solid is formed.
For acidic dissolution of FA, ions of F- were found to dissolve faster (or in a greater ionic proportion) when compared to ions of calcium and orthophosphate[17,68,77,83,88,89]. A similar phenomenon of faster (or in a greater ionic proportion) dissolution of calcium when compared to that of orthophosphate was also found[40,75,76,79-82,90]. In the latter case, a surface layer of acidic calcium orthophosphates, presence of HPO42- ions and/or Ca-depleting of the surface were either suggested[52,61,85] or found[81,86,88,89]. Thus, if incongruent dissolution occurs from a stoichiometric HA surface, the surface Ca/P ratio will become lower than for the bulk and a Ca-deficient HA (CDHA) must then be present, even if there is no phase change[54]. However, there are contradictory results. For example, when FA was dissolved, the solution concentrations of calcium and fluoride ions were non-stoichiometrically lower with respect to that of orthophosphate ions due to a possibility that some amount of sparingly soluble calcium fluoride was precipitated[40,86,88-94]. Furthermore, one should mention on a study, in which release of calcium into the bulk solution was always less, when compared with release of orthophosphate[68]. On the other hand, having followed the release kinetics of calcium and orthophosphate ions into solution, apatites were found to dissolve stoichiometricaly (congruently)[21,73,95].
Interestingly, but apatites might be dissolved stoichiometrically or non-stoichiometrically depending on the experimental conditions. For example, CDHA was found to dissolve congruently at the solution pH < 4.5, while an incongruent dissolution with Ca/P ratio in solution attaining values as high as about 25 was detected in solutions within 4.5 < pH < 8.2. Furthermore, almost negligible dissolution with another type of a non-stoichiometry with Ca/P ratio close to zero in solutions was found at solution pH > 8.2[87]. For 4.5 < pH < 8.2 conditions, the authors explained the incongruent dissolution by re-adsorption of already dissolved orthophosphate anions from the solution onto the positively charged CDHA surface. While in more basic solutions, the surface of CDHA was charged negatively and, thus, the authors suggested a possibility of both re-adsorption of already dissolved calcium cations onto CDHA surface and desorption of orthophosphate ions from the CDHA surface. However, it has to be realized that at solution pH > 8.2 the uncertainties in the chemical analysis of Ca (in particular) and P were relatively high, making any quantitative interpretation of this re-adsorption/desorption difficult[87]. The same effect was discovered in another study[89]. Furthermore, dissolution of both FA and natural sedimentary carbonated FA was found to be incongruent in the early stages but tended toward congruency as the dissolution reaction proceeded to steady state[40,68,96]. According to the authors, this initial incongruency was likely a result of the exchange of solution H+ ion for mineral bound Ca[40]. Besides, a presence of simple inorganic salts (Na2SO4, CH3COONa or NaCl) in solution appeared to have an influence on the equilibrium concentrations of orthophosphate and calcium ions released from apatite: the order of salts increasing orthophosphate in solution was Na2SO4 > CH3COONa > NaCl, while that increasing calcium was opposite[84]. This effect was explained by a specific affinity of some ions (e.g., sulfate) for apatite and might be a reason for transition of congruent to incongruent dissolution in some cases[92-94,97]. Similarly, presence of other compounds might influence the dissolution congruence[98]. Other reasonable explanations might be due to either experimental difficulties in precise following of Ca/P ratio both in the solution and on the crystal surface or differences in chemical and structural compositions of apatites studied by different researchers (both FA and HA are known to be often non-stoichiometric and calcium-deficient, especially on the surface[2-4,87-89,99]).
The idea on a great influence of a surface layer is supported by the data on dissolution of stoichiometric HA (Ca/P = 1.67) in aqueous solutions within pH 4.90-9.94[76]. The authors found that after removal of an irreversible surface, which generated excessive calcium and orthophosphate solution concentrations, further behavior of HA became reproducible. A surface of one atom-layer thickness or less was believed to have formed during the preparation of the solid[76]. On the other hand, dissolution of HA in aqueous medium appeared to be always non-stoichiometric at the beginning, but when the solid was successively equilibrated at any given pH, the solution Ca/P ratio approached a limiting value of 1.67. Once this value was reached, the solid only maintained this solution ratio by dissolving stoichiometricaly[76]. The authors explained these phenomena by a previous history of the samples studied. A similar conclusion was also made in another paper[74]. Thus, the experimental techniques of apatite preparation might have a great influence to stoichiometry/non-stoichiometry of dissolution. This is a serious drawback.
Finally, the results on theoretical analysis of surface layer formation on HA should be reported[85]. The main point of that paper is an idea that both the stoichiometric HA (Ca/P = 1.67) and any non-stoichiometric CDHA (Ca/P ratio within 1.5-1.67) might be described as the same substance. More precisely, there is a continuous amount of intermediate compounds within 1.5 ≤ Ca/P ≤ 1.67 having the same crystal structure which is drawn as a line on the solubility diagram CaO - P2O5 - H2O[85]. Furthermore, according to the authors, at the steady state, both HA and CDHA are dissolved congruently only when both the solution and solid have the same Ca/P ratio. Therefore, any sample of HA and CDHA is dissolved incongruently except the only one solution composition having the similar Ca/P ratio with that particular sample. In all other cases, a surface layer having a Ca/P ratio less than 1.67, which is often used as the indication of incongruent dissolution of apatite, will form as a result (this, however, depends on the accuracy with which the analyses can be made)[85]. Thus, whether apatites are dissolved congruently or incongruently might also depend on both their initial chemical composition and the solution properties.
To conclude, one should notice that all the aforementioned cases of incongruent dissolution of both FA and HA describe the formation of a surface layer of a CDHA and/or acidic calcium orthophosphates, which is calcium-depleted when compared to the bulk apatite. Thus, there is a disagreement between the incongruent dissolution and calcium-rich layer formation model. Perhaps, this might be due to the differences in experimental conditions.
A chemical dissolution model was proposed as well[100-102]. This model was developed from a self-evident supposition that it would be highly unlikely if apatite were dissolved by detachment of “single molecules” equal to the unit cells and consisting of 18 ions. Moreover, in the crystal lattice all ions are shared with neighboring unit cells and often cannot be attributed to the given “single molecule”. Therefore, based on the experimental results obtained on the one hand and an analysis of the data found in references on the other hand, a sequence of four successive chemical reactions:
Ca5(PO4)3(F, OH) + H2O + H+ = Ca5(PO4)3(H2O)+ + HF, H2O (1)
2Ca5(PO4)3(H2O)+ = 3Ca3(PO4)2 + Ca2+ + 2H2O (2)
Ca3(PO4)2 + 2H+ = Ca2+ + 2CaHPO4 (3)
CaHPO4 + H+ = Ca2+ + H2PO4- (4)
was proposed to describe the chemical processes of apatite dissolution[100-102]. According to this model, equations (1)-(4) should be used instead of the well-known net-reactions (5) and (6):
Ca5(PO4)3(F, OH) + 7H+ = 5Ca2+ + 3H2PO4- + HF, H2O (5)
Ca5(PO4)3(F, OH) → 5Ca2+ + 3PO43- + F-, OH- (6)
Chemical model (1)-(4) was initially created for description of apatite dissolution in strong acidic media[101] and appeared to be a further development of some ideas proposed earlier. For example, already in 1960s reactions (5) and (6) had been suggested “not to give the mechanism but merely express net-reactions only”[103]. Later, Pearce[104] and Chow[35] discussed which of net-reactions (5) or (6) described the dissolution process better. For acidic dissolution of apatites, net-reaction (5) represents the direct chemical interaction between the surface of solid apatite and an acidic solution. However, Pearce suggested that, in principle, the dissolution process might also happen according to net-reaction (6) followed by a chemical interaction in the solution among the ions of apatite and acid near the crystal surface[104]:
5Ca2+ + 3PO43- + F-, OH- + 7H+ = 5Ca2+ + 3H2PO4- + HF, H2O (7)
In spite of a lack of the experimental techniques, able to follow the detachment of single ions, a reasonable ionic description of apatite dissolution as a system of chemical equations (1)-(4) was created from the indirect measurements[100-102]. According to this model, chemical dissolution of apatite occurs step by step on the surface via intermediate formation of a mono-atomic layer of some virtual compounds, like Ca3(PO4)2 and CaHPO4[100-102]. Both latter substances are known as precursors of apatite formation during chemical crystallization[3,105]. Moreover, based on the sequence of ionic detachment (first fluorine for FA or hydroxide for HA, followed by calcium and afterwards by orthophosphate) it is suggested that dissolution of apatites is always incongruent (non-stoichiometric) at the atomic (ionic) level. However, a lack of the precise experimental verification transforms the chemical model into a reasonable hypothesis only.
To conclude this model, one may assume that some new relations between the kinetically controlled and chemical models might be established in future. Before the chemical model was created, chemistry of apatite dissolution had been always described by equations (5) or (6) + (7). For this reason, the kinetically controlled model was also adapted for these equations. For example, the overall rate constants for net-reactions (5), (6) and (7) are still used for calculations, whereas they are probably equal to either the lowest of the rate constants of (1)-(4) (the rate determining step) or some combination.
A process of etch pit formation describes acidic dissolution of apatite crystals containing structural defects (dislocations and inclusions)[41-48,96,106-115]. A radius of dislocations outlets (hollow cores) on apatite was calculated to be within 8.3-20 Å for screw dislocations and 18-43 Å for edge ones[109]. The presence of dislocations accelerates dissolution, because dislocations give rise to continuous steps on the surface (Figure 2D) and the strain energy they cause in crystals favors etch pit formation. Thus, the dissolution process of solids is induced by formation of pits (Figure 3) and continues with spreading of their stepwaves[116,117]. As a result, the surface of apatite becomes rough and the total edge length and edge free energy increases[41-48]. These pits provide dissolution sites and the entire reaction proceeds via nucleation and growth of the pits accompanying step flow. The pits appear at the dislocation outlets, usually they are 0.1-10 μm in size (their dimensions depend on dissolution kinetics and dissolution time: they increase when the dissolution progresses; furthermore, the crystals must be sufficiently big to provide enough room for large pits to form). The walls and bottom of etch pits consist of crystal faces possessing the highest dissolution rates, which allow them to grow. However, the growth kinetics of etch pits (therefore, the dissolution process of apatites in general) might be suppressed by addition of very simple chemicals, such as NaCl. This phenomenon might be attributed to a competition for surface protonation sites between Na+ and H+ ions.
For dissolution of apatites, the pits usually have a hexagonal shape (Figure 3) according to the crystal symmetry P63/m of pure HA and FA[106-111,118-123]. However, their shape might be different (e.g., triangular) when specific ions (e.g., fluoride) are present in a solution[121]. It is important to mention that the growing process of etch pits might be inhomogeneous: movement of the dissolution steps on one side of any single pit might be faster or slower their counterparts on the other side, suggesting the formation of asymmetric pits, as schematically shown in Figures 3A and D. Concerning height of the steps, it appears to depend on both crystal faces and dissolution conditions. For example, for an HA (100) surface exposed to deionized water, the average height of each step was found to be 0.84 ± 0.1 nm, which is close to the interlayer distance of the (100) surface [d(100) ≈ 0.82 nm]. Furthermore, it remained constant during dissolution[120].
The formation of etch pits on the crystal faces is the driving force for dissolution. However, in the case of nearly physiological conditions and sufficiently low solution undersaturation, a free energy barrier becomes too high for vacancy nucleation to occur on a time scale that is competitive with other processes. Thus, the dissolution process of apatites becomes spontaneous only when etch pits of critical sizes (determined by the Gibbs-Thomson effect, a well-known thermodynamic principle) are reached[41-48]. At this critical size, the free energy change goes through a maximum that defines an energy barrier to a pit formation. Therefore, only relatively large pits (of sizes greater than a critical value) appear to be active, with stepwaves contributing to dissolution, while the spreading velocities are also dependent on the pit sizes, decreasing with pit size decreasing. Moreover, during dissolution, the crystals become smaller and the average lengths of dissolution steps decrease (which leads to a decrease in dissolution rates) and approach the critical value. When dimensions of dissolving crystals is sufficiently reduced, in some cases dissolution is thought to be dynamically stabilized (dissolution suppression) due to a lack of space for active pits/defects formation on the very small crystallite surfaces[41-48]. This phenomenon involves particle-size-dependent critical conditions of energetic control at the molecular level. Although, the authors claim this effect as “a new dissolution model incorporating particle size considerations”[41-48], in fact, they just have introduced some boundary conditions (the minimal pit sizes and crystal dimensions) to the etch pit formation process. One should remind, that a similar effect of the dissolution self-inhibition was detected by the authors of the calcium-rich layer formation model[19,49-53], although the interpretation of this effect was quite different (see above).
Different acids were used in experimental investigations but, unless the conditions of surface coating creation[124], no specific influence of the acids to etch pit formation and growth was found[106-115]. A theoretical basis for the pit formation and growth at the surface outlets of dislocations includes detachment of single ions from the kink sites. The bulk rate associated with dissolution stepwaves arises quite naturally from the equations describing the spreading of step trains from structure defects and densities[43]. However, until recently, the experimental investigations on pits formation and growth on apatites were made when their dimensions became at least 0.3-0.5 μm and even larger. Smaller dimensions of pits were out of the range of old microscopes. That is why, the initial stages of etch pits formation are not quite clear yet.
The investigations on apatite dissolution using atomic force microscopy provided new data on this point[41-48,66,67,118-122]. For example, the growth process of a single pit on apatite was followed since its dimensions were 50 nm[66,67]. Therefore, one may expect new results on even smaller dimensions of pits to appear soon.
An ion exchange dissolution model is based on a supposition about adsorption of protons[40] and anions of acid (e.g., citrate anions[125-127]) from a solution onto the surface of apatite and removing ions of calcium and orthophosphate into the solution instead. An uptake of citric acid[125] and citrate ions[126] from dilute (4-12.5 mmol/L for citric acid[125] and 0.05-1 mmol/L for sodium citrate[126]) aqueous solutions by a synthetic HA was found to be time independent and follow Langmuir isotherms rather good. However, it was not the case when solutions of higher concentrations were used. In more concentrated solutions (13-100 mmol/L of citrate), this interaction was “reactive” and not “adsorptive”[125].
Adsorption was found to take place by ionic exchange of orthophosphate by citrate ions at the solid-solution interface, caused by a higher affinity of citrate than orthophosphate species for the Ca-sites on the surface. Citrate ions were proposed to interact in two ways: C6H8O73- interacted weakly in a bi-dentate manner (1 citrate per 2 calcium sites), whereas C6H9O72- interacted strongly in a mono-dentate manner (1 citrate per 1 calcium site)[126]. Recent computer simulations revealed that this process is followed by hydrogen-bonded interactions of citric acid to surface oxygen ions of apatites[128]. Furthermore, the adsorbed citrate molecules can use their free carboxylate and hydroxyl groups to self-assemble on the HA surface via intermolecular hydrogen bonding[129].
Later this model was updated by investigation of apatite dissolution in other acids and an adhesion-decalcification concept was introduced[130,131]. According to this concept, the mechanism of acidic interaction with HA was found to involve two phases. In the first phase, an acid bonds to surface calcium of HA with formation of calcium-acid complexes. Depending on both a solubility and a diffusion rate of the calcium-acid complexes from the HA surface to a solution, the acid will in the second phase either remain attached to the HA surface with only limited decalcification involved or the calcium-acid complexes will detach, resulting in a substantial decalcification effect. Rather similar data, in which carboxylic groups of polyalkenoic acid were adsorbed on the surface of an HA substrate, replaced orthophosphate ions and made ionic bonds with calcium ions of HA, were obtained in another study[132].
Recently, ab initio total energy methods were used to study the atomic structure and surface chemistry of HA[133]. All surfaces of HA were found to react strongly with water and a loss of Ca from the surface in exchange for two H appeared to be very favorable. Since these calculations were performed for the case of water adsorption on HA, it remained unclear whether they can be applied to the acidic solutions. Nevertheless, other researchers found this effect experimentally[86,88]. Furthermore, another type of the exchange was proposed for HA, in which one calcium and one hydroxyl were replaced by one proton[87].
To conclude this model, the time independent ionic exchange of orthophosphate by citrate was detected in dilute solutions only. In more concentrated solutions it transferred into chemical reaction (5) followed by time dependent precipitation of calcium citrate when its solubility was exceeded[125,127]. Application of this model to HA dissolution in other acids revealed its dependency on both the solubility and the diffusion rate of the calcium-acid complexes[130,131]. Thus, new experimental data are necessary, to elaborate the ion exchange model further.
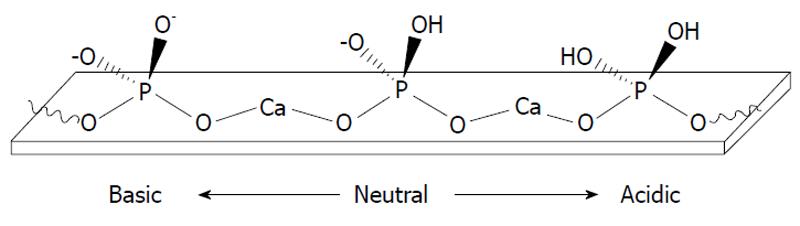
A hydrogen catalytic model is based on a reasonable suggestion about adsorption of protons onto negatively charged oxygen ions of the surface orthophosphate groups of apatites[134]. Sorption of protons results in partial transformation of surface PO43- groups into HPO42- and catalyses the dissolution process[9,10,15,18,20,53-61,89]. A schematic representation of this process at different solution pH is shown in Figure 4[119]. Besides, recent computer simulations revealed that both OH- (for HA) and F- (for FA) located on the surface are protonated as well and, of them, fluoride ions exhibited much lower proton affinities (pKB = 10.8, a weak base) compared to hydroxide (pKB = 0, a strong base)[135]. Furthermore, the surface protonation of apatites is intimately related to hydrogen bonding. The details on the latter process are available in literature[136].
One can notice, that the authors of different dissolution models (the diffusion and kinetically controlled[9,10,15,18,20] and polynuclea[56-61] models) have suggested a similar possibility of a catalytic effect of the adsorbed protons. At present, indirect data only are available to support this hypothesis. Namely, at neutral pH, dissociation of ions is penalized by more than 150 kJ/mol giving rise to very stable apatite-water interfaces[135]. This picture changes drastically with decreasing pH, as the protonation of orthophosphate and hydroxide ions lowers the free energy of calcium ions dissociation. An obvious trend in apatite dissolution is that the dissolution rate is increased as the solution pH decreases, which is a general phenomenon observed in dissolution of other minerals. This indicates that dissolution proceeds by surface protonation, which promotes breaking of Ca-O bonds.
In the course of proton uptake, the charge of the surface anions is reduced and the Coulomb attraction to the crystal surface is lowered considerably, which might be considered as “catalysis”. Currently, no precise information about a catalytic activity of adsorbed protons on the dissolution of apatites is available. However, it does not mean that this effect does not exist. Up to now, nobody has ever succeeded to reveal a catalytic effect unambiguously due to a lack of an experimental technique able to provide the experimental data necessary. Obviously, the general idea on a catalytic activity of the adsorbed protons seems reasonable and, perhaps, this effect will be better elucidated in future.
There is an old tale on six blind men, who wanted to determine what an elephant looked like. An elephant was delivered and the men were allowed to feel different parts of its body. The blind man who felt a leg said the elephant was like a pillar; the one who felt the tail said the elephant was like a rope; the one who felt the trunk said the elephant was like a tree branch; the one who felt an ear said the elephant was like a hand fan; the one who felt the belly said the elephant was like a wall; and the one who felt the tusk said the elephant was like a solid pipe. Thus, six blind men appeared to be in complete disagreement. Then, a wise man explained to them: “All of you are right. The reason every one of you is telling it differently is because each one of you touched the different part of the elephant. So, actually the elephant has all the features you mentioned.” The story is widely used to indicate that the reality may be viewed differently depending upon one’s perspective, suggesting that what seems the absolute truth may be relative due to a deceptive nature of half-truths.
As the complete physical picture that explains widely observed variations in dissolution behavior is still lacking, a similar approach must be adapted to the aforementioned dissolution models of calcium apatites. Undoubtedly, each from the aforementioned models appears to have limitations and drawbacks of its own and none of them is able to describe the apatite dissolution in general. Moreover, most of the models were elaborated for apatite dissolution in either slightly acidic or nearly neutral (4 < pH < 8) aqueous solutions, relatively small values of solution undersaturation and temperatures of 25 °C and 37 °C only. Nothing is known about the validity of these models for apatite dissolution in strong inorganic acids (HCl, HNO3, H2SO4, H3PO4) for solution pH < 2 and temperatures above 70 °C. Moreover, in such “tough” experimental conditions, the numerical value of solution undersaturation by HA and FA becomes uncertain due to impossibility to determine their solubility[1-4]. The latter cases serious problems for application of current versions of calcium-rich layer formation and polynuclear models to apatite dissolution in strong acids, because both models operate with the solution supersaturation/undersaturation phenomena. The abovementioned “tough” dissolution conditions are common in industry of fertilizer production[137] and have to be taken into account by the final version of any dissolution model.
However, there are no doubts that each of the models discussed is correct for the specific experimental conditions studied. The different models are just devoted to diverse aspects of the same process of apatite dissolution and are likely complement each other. Undoubtedly, the dissolution process of calcium apatites has all the features elaborated within eight dissolution models. Unfortunately, it is still impossible to obtain the complete understanding for all the processes involved because experimental techniques able to provide direct following after diffusion, sorption, detachment and transformation of the single atoms, ions and molecules currently are lacking. Therefore, researchers are still forced to make conclusions about the events happening at the atomic (ionic) level based on indirect measurements and/or calculations only. That is why, combining the experimental and theoretical findings, obtained by different investigators (often under hardly comparable experimental conditions), currently, seems to be the only way to create a general depiction of the dissolution mechanism of calcium apatites in acids.
At the fundamental level reactions between solids and liquids involve a coupled sequence of mass transport, adsorption/desorption phenomena, heterogeneous reaction, chemical transformations of intermediates, etc., whose identification, separation and kinetic quantification are all necessary if the mechanism of the process is to be fully understood and described[138]. It is also generally agreed that during dissolution lattice ions undergo the following processes: (1) detachment from a kink site, (2) surface diffusion away from the crystal steps, (3) desorption from the surface and (4) diffusion into the bulk solution[139]. Therefore, the steady-state conditions of apatite dissolution in aqueous acidic media include the following simultaneous processes or steps: (1) diffusion of chemical reagents (H+ and anions of acid An-) from bulk solution to the solid/liquid interface; (2) adsorption of the chemicals onto the surface of apatite; (3) chemical transformations on the surface; (4) desorption of products (ions of fluoride, calcium and orthophosphate) from the crystal surface; and (5) their diffusion into the bulk solution.
All the steps mentioned above are likely to be much more complicated. For example, processes 1 and 5 include chemical transformations happen with the ions during diffusion, because solution pH is known to depend on the distance from the solid/liquid interface (in acidic solutions it is higher near the surface of apatite and decreases when the distance increases)[140,141]. Processes 2 and 4 include ionic diffusion along the surface both to (step 2a) and away from (step 4a) the crystal steps, respectively, as well as a diffusive jump (steps 2b and 4b)[139]. Finally, process 3 consists of several successive chemical transformations [step 3a - chemical equations (1)-(4)][100-102] and includes ionic detachment from the kink sites (step 3b)[139]. Moreover, for adsorption (step 2) to take place, the following intermediate steps are necessary: (1) dehydration of a surface site; (2) partial dehydration of ions; and (3) a diffusive jump toward the surface[139]. One can also expect three similar intermediate steps (diffusion jump from the surface, hydration both the ions and the surface site) for desorption (step 4).
As shown above, different models describe just diverse aspects of the same phenomenon of apatite dissolution. Commonly, the main distinction is made between the transport control and surface-reaction control. For example, in the diffusion controlled, two-site and polynuclear models steps 1 and 5 limit a reaction rate. On the contrary, in the kinetically controlled, chemical and hydrogen catalytic models a reaction rate is limited by step 3. In the cases of the ion exchange and self-inhibition (or calcium-rich layer formation) models, a reaction rate is likely to be controlled by both ionic diffusion (steps 1 and 5) and kinetics of the adsorption/desorption phenomena (steps 2 and 4). Processes of etch pit formation and dissolution stoichiometry - are the experimental facts, not models. Thus, they may be controlled by factors pertaining to any step from 1-5 and even all of them.
Briefly, crystals of HA and FA consist of individual orthophosphate tetrahedra linked by calcium cations. The orthophosphate groups forms the skeleton having two types of calcium sites. The first [Ca(1) site] is occupied by four calcium atoms that have a nine-fold coordination, while the second [Ca(2) site] is occupied by six calcium atoms having a seven-fold coordination. Fluoride (for FA) or hydroxide (for HA) anions are located within the same channels as the Ca(2) sites and have a high mobility[1-4,142,143]. Thus, the apatite structure contains Ca-F (for FA), O-H (for HA), Ca-O and P-O bonds; consideration of the relative electrostatic strength of these bonds suggests that their relative destruction rate is consistent with: Ca-F ≈ Ca-OH > Ca(1)-O > Ca(2)-O > P-O. Considering its structure, once all Ca-F and Ca-O bonds are broken, apatite is destroyed; while breaking of P-O bonds is unnecessary for apatite dissolution[96].
When apatite comes into a contact with an acidic aqueous solution, dissolution steps 1-5 (see section 4) begin. Before giving the detailed description of the processes involved, the following assumptions and limitations must be made: (1) the stoichiometric apatite (Ca/P = 1.67) is dissolved and neither non-stoichiometric layers nor other ions except of calcium, orthophosphate, hydroxide (for HA) or fluoride (for FA) are initially present in the crystal lattice, whereas volume and surface defects (dislocations and dislocation outlets respectively) might be present and, if present, they are distributed randomly; (2) except of the presence of dislocation outlets, the initial surface of apatite is perfect (molecularly sooth). Otherwise, each imperfection might act as a possible dissolution nucleus; (3) in spite of the limitations and drawbacks discussed above, all the afore-discussed dissolution models are correct and complementary to each other; (4) in some cases, anions of acid might have an influence on apatite dissolution due to a specific affinity (e.g., citrate) or by means of formation of insoluble compounds (e.g., sulfate, fluoride). That is why, anions are specified neither here nor below. It is just assumed that dissolution of apatite occurs in acid HnA, where An- is an anion; (5) only soluble compounds are formed during the apatite dissolution in acids. No precipitates are obtained; (6) hydration effects for all the ions and molecules involved as well as those for crystal surface of apatite[99,144-148] are omitted for simplicity; (7) all crystal faces of a solid apatite are equal and have a similar ionic arrangement. Although, it was found that HA (001) facets could be more resistant against acidic dissolution than (100) ones[149], no specific influence of different crystal faces on the dissolution process is considered; and (8) since the afore-described dissolution models have been elaborated for micron-sized apatite crystals, while the nanodimensional calcium orthophosphates possess the special properties[150,151], to eliminate the size effects, dissolution of large crystals is described. No specific influence of crystal dimensions on the dissolution mechanism is considered.
Based on these assumptions and limitations, an attempt to create the general description of the apatite dissolution mechanism at the atomic (ionic) level is given below.
Immediately after being placed to acidic aqueous solutions, the surface of apatite crystals becomes in contact with water molecules and ions of the acid, which results in sorption of all these chemicals with simultaneous formation of a solid/liquid interface and various adjacent strata, such as a Nernst diffusion layer, an electrical double layer, etc. Transport of the chemicals (H+ and An-) to the solid/liquid interface always happens by ionic diffusion through the Nernst diffusion layer (Figure 1). A thickness of this layer depends on both solution hydrodynamics and dimensions of the crystals dissolving: it decreases when agitation intensity increases and crystal sizes decrease. However, in no cases the thickness becomes equal to the zero[152]. Thus, a concentration gradient is always present near the solid/liquid interface, the diffusion laws always remain valid and all findings of the diffusion-controlled model (e.g., an adsorption resistance and a diffusion jump) remain applicable for any case of apatite dissolution. A similar approach is correct for the surface phenomena: when dissolution occurs, adsorption and desorption of ions, as well as chemical transformations (1)-(4) always take place on the surface regardless the experimental conditions chosen.
After being delivered by diffusion to the solid/liquid interface, ions of H+ and An- are adsorbed onto the surface of apatite. A great number of various surface complexes might be formed as a result[86-89,153-155]. According to the diffusion-controlled model, there is an adsorption resistance for ions to be adsorbed onto the surface and in order to overcome the resistance the ions make a diffusive jump toward the surface to a distance corresponding to their size[139,156]. Being charged positively, protons are adsorbed onto oxygen ions of orthophosphate groups[58] as well as onto ions of fluoride (in the case of FA) and hydroxide (in the case of HA). After the model by Wu et al[153], the surface protonation of apatites proceeds via formation of ≡POH surface groups (“≡” stands for the surface) at 5 < pH < 7, while apatite surfaces become fully protonated at pH < 5. One may expect to find some differences in the adsorption kinetics of protons onto fluoride, hydroxide and orthophosphate ions. Namely, due to a higher electro negativity of fluoride (when compared to oxygen ions of orthophosphate groups) and a higher basicity of hydroxide (when compared to orthophosphate), adsorption of protons might happen faster (or previously) onto these ions when compared with orthophosphate. However, recent results of computer simulations indicated a possibility of OH- protonation by the nearest HPO42- ion[135], indicating to the fact, that orthophosphate ions might be protonated faster (or previously) if compared to that for hydroxide ions. Obviously, this topic needs to be clarified in future.
Anyway, negatively charged anions An- may be adsorbed onto calcium cations only. According to the ion exchange model, the exchange process shows an adsorption of about one anion per unit-cell of apatite[125-127]. On the other hand, the surface of apatites is charged positively in aqueous acidic media and negatively in basic solutions (the point of zero charge is at solution pH within 6.8-8.5) with an electric double layer formation at the solid/liquid interface[70-72,78,86-88,153-155,157,158]. The latter points out to a non-equivalent ionic adsorption of H+ and An- onto apatite: in acidic solutions, adsorption of protons always exceeds that of An-, while in basic solutions the situation is opposite. Therefore, in acidic solutions there is at least one extra-adsorbed proton per several neighboring unit-cells of apatite when compared to the number of adsorbed anions. The fact of a non-equivalent ionic adsorption might be explained by differences in sizes and mobility between H+ and An-[159]. Great difference in the surface sites available is another reason for the non-equivalent ionic adsorption. Namely, the concentration of the lattice ions being on the surface of HA were found to be equal to 2.57, 3.02 and 4.50 ions/nm2 for OH-, PO43- and Ca2+, respectively[69]. Furthermore, according to drawings of the apatite structure, the most part of its surface (up to 80%-90%) is covered by oxygen ions of orthophosphate groups[160].
Ions of the crystal lattice of apatites are known to have different crystallographic positions: so-called X-ions (F-, OH-, Cl- and substitutes for them) are located in Ca(2) channels parallel to c-axis[1-4,142,143]. This position results in a relatively high mobility of X-ions: for example, they might be mutually substituted rather easily [88,89,161-163] with formation of intermediate compounds, like fluorhydroxyapatites or hydroxyfluorapatites[17,83,164]. Based on these findings, dissolution of apatite in acids was suggested to start with detachment of X-ions (more likely, as HX) from the surface[100-102] followed by their diffusion away from the crystal steps and further into the bulk solution[139,156]. Recent computer simulations revealed some differences in the dissolution kinetics between F- and OH- anions in apatites: surface fluoride is dissolved not as readily as hydroxide is[143]. Initial leaving of X-ions was also detected in the incongruent dissolution model[17,68,77,83,88,89]. Moreover, numerical values for the surface tension found for dissolution of HA appeared to be clearly lower than those found for HA growth (the polynuclear model). The latter data were explained by partial protonation of orthophosphate groups and missing of some hydroxide ions on the crystal surface[60].
After detachment of X-ions from the surface, there are calcium, orthophosphate, H+ (as HPO4 and/or H2PO4 groups) and An- ions left on it (hydration effect is omitted for simplicity). From now on, any differences between FA and HA disappear. In any cases, adsorption of protons onto calcium is impossible due to charge repulsion. Therefore, an electrical double layer with a positive charge on apatite cannot be continuous at the atomic (ionic) scale. There should be local uncharged places in it, say, at the positions of calcium cations. According to the chemical model, an interaction between calcium cations and anions of acid adsorbed from a solution is believed to happen in such places[100-102]. This interaction results in breaking of surface ≡O-Ca bonds (“≡” stands for the surface) and detachment of some calcium from the kink sites followed by their diffusion away from crystal steps and further into the bulk solution (the diffusion-controlled model[139,156]). Detachment of calcium might occur as calcium-acid complexes (the ion exchange model). Recent computer simulations revealed that a local excess charge of +3 and +4 must be created to cause exothermic Ca2+ displacement from Ca(1) and Ca(2) cites, respectively[135]. If so, under otherwise equal conditions, detachment of Ca2+ ions from Ca(1) cites of the apatite surface should happen faster and/or easily than that from Ca(2) cites.
Detachment of calcium ions results in formation of dissolution nuclei. These nuclei are defined as collections of vacant sites for Ca2+, PO43- and X- ions on the crystal surface of apatite[56]. According to the polynuclear model, removal even of one ion might result in further dissolution because critical nuclei (x*) were calculated to consist of 1-26 ions for dissolution of HA and 0.3-34 ions for dissolution of FA. (According to the authors, x* < 1 means that there is no nucleation barrier to be overcome[61]. Since one unit cell of apatite contains 18 ions, x* > 18 means that more than one unit cell should be dissolved for a nucleus to form). The numeric values for x* were found to depend on solution pH and solution undersaturation[60,61]. Furthermore, due to charge repulsion, adsorbed protons (as HPO4 and/or H2PO4 groups) might catalyze detachment of calcium ions from the kink sites (the hydrogen catalytic model).
After being detached, calcium cations [possibly, as calcium-acid complexes (the ion exchange model)] diffuse along the surface away from the dissolution steps before entering the solution[139]. For dissolution of octacalcium phosphate (OCP): [Ca8(HPO4)2(PO4)4·5H2O] in slightly acidic (pH = 5.66) solutions numeric values for the mean surface diffusion distance of the lattice ions detached from steps were calculated. These values were found to depend on the edge free energy and be within (17 ± 4)α– (41 ± 10)α, where α ≈ 3.7 Å is the size of a growth unit (or mean ionic diameter)[156]. Numeric values of mean ionic diameter for apatites were also calculated. They appeared to be less than that for OCP: 3.09 Å for HA and 3.07 Å for FA[62]. Taking into the consideration great similarities found between the chemical composition and crystal structures of OCP and HA[165], one might assume that the numerical values of surface diffusion distance for HA should be close to the values for OCP.
Ionic detachment of some calcium results in removing of a local positive charge from apatite, which is immediately compensated by adsorption of other protons from the acidic solution. This conclusion is based on the surface charge measurements: no information on influence of dissolution time to values of the surface charge on apatite has been found in literature[70-72,78,86-88,153-157]. So, one may assume, that if a chemical composition of the solution is kept constant the surface charge on apatite will also remain constant during dissolution. Replacement of calcium by protons results in formation of mono-atomic layer acidic calcium orthophosphates on the crystal surface. Chemical phenomena of these transformations are described by the chemical model[100-102] and the kinetics (it strongly depends on the experimental conditions chosen) - by the surface controlled model.
After being desorbed from the surface, calcium cations (presumably, coupled with anions An-) diffuse through the Nernst layer into the bulk solution (the diffusion controlled model)[139,156]. However, according to the calcium-rich layer formation model, a part of the already dissolved calcium ions might be adsorbed back onto apatite. Adsorption of calcium was suggested to happen at the very beginning of dissolution only and resulted in formation of a perm-selective layer of calcium cations with or without counter ions (An- and/or acidic orthophosphate)[19,49-53,68]. In this case, there should be a competition between protons and calcium cations for the exposed ions of oxygen on the surface to be adsorbed onto. Experimental data on a shift of the point of surface zero charge into more basic solution pH in presence of calcium in a solution[157] are in favor of such competition.
An idea on formation of some layer on the surface of apatite was raised in several dissolution models. For example, there is either a supposition (the polynuclear, diffusion and kinetically controlled models) or a description (the ion exchange, hydrogen catalytic and chemical models) of a very thin virtual layer of acidic calcium orthophosphates (more exactly presence of HPO42- ions) on the surface of apatite. Besides, according to the calcium-rich layer formation model, dissolution of apatite happens by ionic diffusion through a layer containing calcium with or without counter ions[19,49-53,68]. In part, this idea can be found within the ion exchange model where a monolayer of calcium citrate[125-127] and/or calcium-acid complexes[130,131] are assumed to form onto apatite during dissolution. However, no other model requires such suggestion. According to the rest of them, formation of any calcium containing compounds (different from acidic orthophosphates) on apatite is not discussed at all.
According to the chemical model, the initial stages of apatite dissolution consist of calcium detachment from the surface and incorporation of protons instead. Orthophosphate groups are assumed to keep their positions without any relocation[100-102]. Due to the fact, that calcium occupies definite lattice positions, whereas protons are bound to oxygen ions of orthophosphate groups, removing of each calcium results in decreasing of attraction forces between the nearest (to this calcium) orthophosphate group and rest part of the crystals. When all (or almost all) neighboring cations of calcium have been removed, orthophosphate groups (as H2PO4-, CaH2PO4+ or H3PO4 - it is not clear yet) also detach from the surface. Then they diffuse along the surface away from the dissolution steps before entering the solution as described above for calcium[139,156].
In the case of crystal faces with perfectly smooth surface (dissolution steps are absent), detachment of one or several ions results in formation of dissolution nuclei, which the polynuclear model is based on[55-63]. According to this model, all sites in nuclei edges are the kink positions[62] and, after appearance, the nuclei grow and spread over the surface with a definite lateral rate[56], giving rise to formation of dissolution steps. If dissolution steps already existed on the crystal faces of apatite, detachment of one calcium or one orthophosphate would result in dissolution step movement jump-wise over a distance equal to the sizes of these ions (approximately for 1 and 3 Å, respectively).
The latter is also valid for dissolution of crystal edges and corners. Since the classical paper by Kaischew[166], it is generally considered, that ions are less strongly bound along edges of a crystal than in the middle of faces and still less strongly at the corners[167]. No information about the ionic arrangements on edges and corners of apatite crystals has been found in literature. Therefore, two boundary conditions are possible: the edges and corners mainly consist of ions of either calcium or orthophosphate. However, the edges parallel to the c-axis, in principle, may consist of X-ions (F-, OH-, Cl-). The last case is the simplest one. According to the chemical model[100-102], dissolution of apatite starts with protonation and detachment of X-ions, followed by removing of calcium (one should remind here that “walls” of the channels where X-ions are located consist of Ca(2) ions[96]) and afterwards by protonation and removing of orthophosphate. In the case, when the edges and corners of apatite mainly consist of calcium, again, according to the chemical model, detachment of weakly bounded calcium precedes protonation and removing of orthophosphate. Finally, if the edges and corners mainly consist of orthophosphate, the dissolution will start by chemical interaction of protons with these weakly bounded orthophosphate groups. The latter decreases electrostatic attraction forces between orthophosphate anions and neighboring calcium cations (attraction forces between Ca2+ and PO43- are evidently stronger when compared with those between Ca2+ and HPO42-). These forces become still weaker after adsorption of the second proton onto the given orthophosphate anion, causing its transformation to H2PO4- followed by detachment.
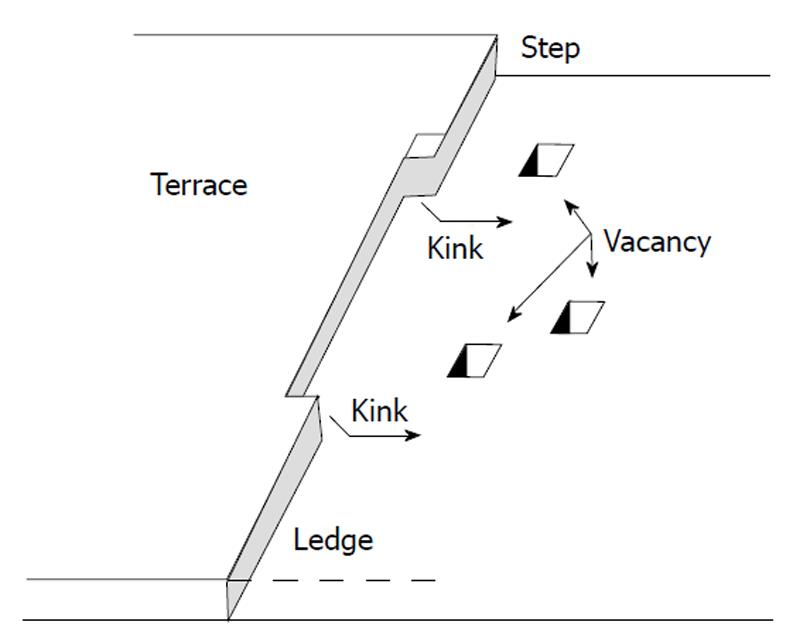
Before now, no data on crystal defects have been used. For this reason, the above description is valid for dissolution of the perfect single crystals without defects and with the molecularly smooth surface. However, like other solids, crystals of apatite always contain both surface irregularities (e.g., steps, missing ions and dislocation outlets) and structural defects inside the bulk of crystals (e.g., dislocations and inclusions). The schematic depiction of a crystal surface is shown in Figure 5. This model is known as the “Kossel model”[168]. In principle, any surface irregularities may act as dissolution nuclei because sometimes even one missing ion might become the critical nuclei (the polynuclear model)[60,61].
Each dislocation outlet on apatite was found to be a hollow core with radius within 8.3-20 Å for the screw dislocations and even 18-43 Å for the edge ones[109]. Dimensions of the hexagonal unit-cell of apatite are: a ≈ 9.43 Å, c ≈ 6.88 Å. If the numeric values for the dislocation outlets were calculated correctly, their dimensions (diameter of the hollow cores) would be 1.8-4.2 times a or 2.4-5.8 times c (for the screw dislocations) and even 3.8-9.1 times a or 5.2-12.5 times c (for the edge dislocations). Thus, each dislocation outlet on the crystal surface looks like a large dissolution nucleus equal to detachment of 3-19 unit cells, (if this is taken to be the product ac) for the screw dislocations and even of 15-90 unit cells for the edge ones.
The process of etch pits formation and growth on apatites was described in details elsewhere[41-48,66,67,106-122]. In the case of single crystals of pure HA, an acid attack was found to start formation of one etch pit in the basal plane which was the preferred dissolution spot or active site. Immediately afterwards the acid formed a longitudinal hole parallel to the c-axis[110]. On the contrary, dissolution of natural FA was found to happen with formation of a great number of etch pits (about 5 × 105 cm-2) on the surface (Figure 6)[113-115]. The latter just points out to the great differences in amount of crystal defects and impurities between the chemically pure[41-48,66,67,106-112,118-122] and natural[113-115] apatites.
In any case, after being formed, the pits were found to grow in all directions (length, width and depth - see Figure 3) with definite rates until they either covered all crystal faces of apatite (dissolution of natural crystals[113-115]) or made longitudinal holes parallel to the c-axis (dissolution of the single crystals of pure HA[106-111]). However, according to “a new dissolution model incorporating particle size considerations”, the dissolution process becomes spontaneous only when the pits are reached the critical sizes[41-48]. The unit-step movement of etch pit growth was suggested to consist of removing of a single ion, followed by surface diffusion away from the place of ionic detachment, desorption from the surface and diffusion into the bulk solution. All these processes evidently occur according to the basic findings of the ion exchange, chemical, calcium-rich layer formation, hydrogen catalytic and diffusion controlled dissolution models.
To conclude this part, except the dissolution rates increasing and surface etching, no other influences of dislocations on the dissolution mechanism were found.
Thus, based on eight dissolution models drawn from the previously published papers, an attempt to create the general description of apatite dissolution process at the atomic (ionic) level has been made. This dissolution mechanism is based on current level of knowledge and will be updated, corrected and modified simultaneously with appearance of new experimental data. Now some missing and unclear points to be investigated in future can be outlined: (1) chemical transformations happening with all ions during diffusion through the Nernst layer; (2) chemical composition of the apatite surface during dissolution; (3) processes of ionic sorption and detachment; (4) processes of dissolution nuclei formation and growth; (5) initial stages of etch pits formation at the dislocation outlets; and (6) specific influence of anions to the ionic sorption, surface diffusion and detachment.
The above topics should be investigated in order to have better understanding of all the processes involved. For example, atomic force microscopy and phase shift interferometry might be useful tools in investigations on dissolution nuclei and etch pits formation[66,67]. Micron-sized (better nano-sized) electrodes might be helpful in studying ionic transformations during diffusion through the Nernst layer[140]. Modern techniques of the surface state analysis might be helpful in understanding the surface structure and its chemical composition.
Peer reviewer: Qing Wu, MD, ScD, Assistant Professor of Biostatistics, College of Medicine, Mayo Clinic, 13400 E Shea Blvd, Scottsdale, AZ 85259, United States
S- Editor Wang JL L- Editor A E- Editor Li JY
| 1. | McConnell D. Apatite: its crystal chemistry, mineralogy, utilization, and geologic and biologic occurrences. Applied Mineralogy, Vol 5. Vienna and New York, USA: Springer-Verlag 1973; 111 pp. [Cited in This Article: ] |
| 2. | Aoki H. Science and medical applications of hydroxyapatite. Tokyo, Japan: JAAS 1991; 245 pp. [Cited in This Article: ] |
| 3. | Elliott JC. Structure and chemistry of the apatites and other calcium orthophosphates. Studies in inorganic chemistry, Vol. 18. Amsterdam, Netherlands: Elsevier 1994; 389 pp. [Cited in This Article: ] |
| 4. | LeGeros RZ. Calcium phosphates in oral biology and medicine. Monographs in Oral Science. Vol. 15. Basel: Karger 1991; 201 pp. [Cited in This Article: ] |
| 5. | Dorozhkin SV. Medical application of calcium orthophosphate bioceramics. BIO. 2011;1:1-51. [DOI] [Cited in This Article: ] [Cited by in Crossref: 75] [Cited by in F6Publishing: 75] [Article Influence: 5.8] [Reference Citation Analysis (0)] |
| 6. | Dorozhkin SV. Calcium orthophosphates: occurrence, properties, biomineralization, pathological calcification and biomimetic applications. Biomatter. 2011;1:121-164. [DOI] [Cited in This Article: ] |
| 7. | Dorozhkin SV. Biocomposites and hybrid biomaterials based on calcium orthophosphates. Biomatter. 2011;1:3-56. [DOI] [Cited in This Article: ] [Cited by in Crossref: 109] [Cited by in F6Publishing: 66] [Article Influence: 6.6] [Reference Citation Analysis (0)] |
| 8. | March J. March’s advanced organic chemistry: reactions, mechanisms, and structure. 5th Ed. New York: Wiley 2001; 2083 pp. [Cited in This Article: ] |
| 9. | Nancollas GH. Physicochemistry of demineralization and remineralization. J Dent Res. 1974;53:297-302. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 13] [Cited by in F6Publishing: 13] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 10. | Wu MS, Higuchi WI, Fox JL, Friedman M. Kinetics and mechanism of hydroxyapatite crystal dissolution in weak acid buffers using the rotating disk method. J Dent Res. 1976;55:496-505. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 44] [Cited by in F6Publishing: 43] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 11. | Smith AN, Posner AM, Quirk JP. A model describing the kinetics of dissolution of hydroxyapatite. J Coll Interf Sci. 1977;62:475-494. [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 20] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 12. | Okazaki M, Moriwaki Y, Aoba T, Doi Y, Takahashi J. Dissolution rate behavior of fluoridated apatite pellets. J Dent Res. 1981;60:1907-1911. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 11] [Cited by in F6Publishing: 11] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 13. | Crommelin DJ, Higuchi WI, Fox JL, Spooner PJ, Katdare AV. Dissolution rate behavior of hydroxyapatite-fluorapatite mixtures. Caries Res. 1983;17:289-296. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 20] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 14. | Nelson DG, Featherstone JD, Duncan JF, Cutress TW. Effect of carbonate and fluoride on the dissolution behaviour of synthetic apatites. Caries Res. 1983;17:200-211. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 78] [Cited by in F6Publishing: 79] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 15. | Higuchi WI, Cesar EY, Cho PW, Fox JL. Powder suspension method for critically re-examining the two-site model for hydroxyapatite dissolution kinetics. J Pharm Sci. 1984;73:146-153. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 20] [Cited by in F6Publishing: 20] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 16. | Budz JA, LoRe M, Nancollas GH. Hydroxyapatite and carbonated apatite as models for the dissolution behavior of human dental enamel. Adv Dent Res. 1987;1:314-321. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 29] [Cited by in F6Publishing: 29] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 17. | Wong L, Cutress TW, Duncan JF. The influence of incorporated and adsorbed fluoride on the dissolution of powdered and pelletized hydroxyapatite in fluoridated and non-fluoridated acid buffers. J Dent Res. 1987;66:1735-1741. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 39] [Cited by in F6Publishing: 40] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 18. | Budz JA, Nancollas GH. The mechanism of dissolution of hydroxyapatite and carbonated apatite in acidic solutions. J Cryst Growth. 1988;91:490-496. [DOI] [Cited in This Article: ] |
| 19. | Thomann JM, Voegel JC, Gramain P. Kinetics of dissolution of calcium hydroxyapatite powder. III: pH and sample conditioning effects. Calcif Tissue Int. 1990;46:121-129. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 42] [Cited by in F6Publishing: 40] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 20. | Chin KOA, Nancollas GH. Dissolution of fluorapatite. A constant-composition kinetics study. Langmuir. 1991;7:2175-2179. [DOI] [Cited in This Article: ] |
| 21. | Margolis HC, Moreno EC. Kinetics of hydroxyapatite dissolution in acetic, lactic, and phosphoric acid solutions. Calcif Tissue Int. 1992;50:137-143. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 76] [Cited by in F6Publishing: 79] [Article Influence: 2.5] [Reference Citation Analysis (0)] |
| 22. | Paschalis EP, Wikiel K, Nancollas GH. Dual constant composition kinetics characterization of apatitic surfaces. J Biomed Mater Res. 1994;28:1411-1418. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 16] [Cited by in F6Publishing: 16] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 23. | Calmanovici CE, Gilot B, Laguerie C. Mechanism and kinetics for the dissolution of apatitic materials in acid solutions. Brazilian J Chem Eng. 1997;14:95-102. [DOI] [Cited in This Article: ] [Cited by in Crossref: 8] [Cited by in F6Publishing: 9] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 24. | Mohammadi Z, Ziaei-Moayyed AA, Sheikh-Mehdi Mesgar A. In vitro dissolution of plasma-sprayed hydroxyapatite coatings with different characteristics: experimental study and modeling. Biomed Mater. 2008;3:015006. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 17] [Cited by in F6Publishing: 17] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 25. | van der Sluis S, Meszaros Y, Marchee WGJ, Wesselingh HA, van Rosmalen GM. The digestion of phosphate ore in phosphoric acid. Ind Eng Chem Res. 1987;26:2501-2505. [DOI] [Cited in This Article: ] [Cited by in Crossref: 38] [Cited by in F6Publishing: 41] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 26. | Dobrydnev SV, Pochitalkina SA, Bogach VV, Beskov VS. Ionometric study of the kinetics of acid decomposition of fluorapatite. Russ J Appl Chem. 2001;74:1627-1630. [DOI] [Cited in This Article: ] |
| 27. | Dobrydnev SV, Beskov VS, Bogach VV, Pochitalkina IA. Ionometric study of the acid decomposition of phosphate minerals. Theoret Found Chem Eng. 2001;35:292-297. [DOI] [Cited in This Article: ] |
| 28. | Dobrydnev SV, Bogach VV, Beskov VS. Analysis of the mass transfer in acid decomposition of phosphorus-containing raw material. Theoret Found Chem Eng. 2003;37:601-605. [DOI] [Cited in This Article: ] |
| 29. | Dobrydnev SV, Bogach VV, Kol’tsova EM, Beskov VS. Effect of the charge of solid particles on the activation energy of acid decomposition of phosphorus-containing raw material. Theoret Found Chem Eng. 2005;39:415-418. [DOI] [Cited in This Article: ] [Cited by in Crossref: 1] [Cited by in F6Publishing: 1] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 30. | Brahim K, Antar K, Khattech I, Jemal M. Effect of temperature on the attack of fluorapatite by a phosphoric acid solution. Scientific Research and Essays. 2008;3:035-039. [Cited in This Article: ] |
| 31. | Fawzi MB, Fox JL, Dedhiya MG, Higuchi WI, Hefferren JJ. A possible second site for hydroxyapatite dissolution in acidic media. J Coll Interf Sci. 1978;67:304-311. [DOI] [Cited in This Article: ] [Cited by in Crossref: 22] [Cited by in F6Publishing: 16] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 32. | Fox JL, Higuchi WI, Fawzi MB, Wu MS. A new two-site model for hydroxyapatite dissolution in acidic media. J Coll Interf Sci. 1978;67:312-330. [DOI] [Cited in This Article: ] [Cited by in Crossref: 39] [Cited by in F6Publishing: 39] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 33. | Griffith EN, Katdare A, Fox JL, Higuchi WI. Transmission electron microscopic confirmation of the morphological predictions of the two-site model for hydroxyapatite dissolution. J Coll Interf Sci. 1978;67:331-335. [DOI] [Cited in This Article: ] [Cited by in Crossref: 9] [Cited by in F6Publishing: 9] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 34. | Ehrlich H, Koutsoukos PG, Demadis KD, Pokrovsky OS. Principles of demineralization: modern strategies for the isolation of organic frameworks. Part II. Decalcification. Micron. 2009;40:169-193. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 81] [Cited by in F6Publishing: 54] [Article Influence: 3.4] [Reference Citation Analysis (0)] |
| 35. | Chow LC. Response to Dr. E.I.F. Pearce’s letter to the Editor. J Dent Res. 1988;67:1058-1059. [DOI] [Cited in This Article: ] [Cited by in Crossref: 4] [Cited by in F6Publishing: 4] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 36. | Tomson MB, Nancollas GH. Mineralization kinetics: a constant composition approach. Science. 1978;200:1059-1060. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 324] [Cited by in F6Publishing: 328] [Article Influence: 23.4] [Reference Citation Analysis (0)] |
| 37. | Tang R, Henneman ZJ, Nancollas GH. Constant composition kinetics study of carbonated apatite dissolution. J Cryst Growth. 2003;249:614-624. [DOI] [Cited in This Article: ] |
| 38. | Tang R, Hass M, Wu W, Gulde S, Nancollas GH. Constant composition dissolution of mixed phases. II. Selective dissolution of calcium phosphates. J Coll Interf Sci. 2003;260:379-384. [DOI] [Cited in This Article: ] [Cited by in Crossref: 48] [Cited by in F6Publishing: 47] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 39. | Ebrahimpour A, Zhang J, Nancollas GH. Dual constant composition method and its application to studies of phase transformation and crystallization of mixed phases. J Cryst Growth. 1991;113:83-91. [DOI] [Cited in This Article: ] |
| 40. | Guidry MW, Mackenzie FT. Experimental study of igneous and sedimentary apatite dissolution: control of pH, distance from equilibrium, and temperature on dissolution rates. Geochim Cosmochim Acta. 2003;67:2949-2963. [DOI] [Cited in This Article: ] |
| 41. | Tang R, Nancollas GH, Orme CA. Mechanism of dissolution of sparingly soluble electrolytes. J Am Chem Soc. 2001;123:5437-5443. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 70] [Cited by in F6Publishing: 70] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 42. | Tang R, Wang L, Orme CA, Bonstein T, Bush PJ, Nancollas GH. Dissolution at the nanoscale: self-preservation of biominerals. Angew Chem Int Ed. 2004;43:2697-2701. [DOI] [Cited in This Article: ] [Cited by in Crossref: 83] [Cited by in F6Publishing: 86] [Article Influence: 4.3] [Reference Citation Analysis (0)] |
| 43. | Tang R, Wang L, Nancollas GH. Size-effects in the dissolution of hydroxyapatite: an understanding of biological demineralization. J Mater Chem. 2004;14:2341-2346. [DOI] [Cited in This Article: ] [Cited by in Crossref: 52] [Cited by in F6Publishing: 51] [Article Influence: 2.6] [Reference Citation Analysis (0)] |
| 44. | Tang R, Orme CA, Nancollas GH. Dissolution of crystallites: surface energetic control and size effects. Chemphyschem. 2004;5:688-696. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 38] [Cited by in F6Publishing: 38] [Article Influence: 2.0] [Reference Citation Analysis (0)] |
| 45. | Wang LJ, Tang R, Bonstein T, Bush P, Nancollas GH. Enamel demineralization in primary and permanent teeth. J Dent Res. 2006;85:359-363. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 82] [Cited by in F6Publishing: 82] [Article Influence: 4.6] [Reference Citation Analysis (0)] |
| 46. | Wang L, Nancollas GH. Calcium orthophosphates: crystallization and dissolution. Chem Rev. 2008;108:4628-4669. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 736] [Cited by in F6Publishing: 453] [Article Influence: 28.3] [Reference Citation Analysis (0)] |
| 47. | Wang L, Nancollas GH. Pathways to biomineralization and biodemineralization of calcium phosphates: the thermodynamic and kinetic controls. Dalton Trans. 2009;2665-2672. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 83] [Cited by in F6Publishing: 86] [Article Influence: 5.7] [Reference Citation Analysis (0)] |
| 48. | Wang L, Nancollas GH. Dynamics of Biomineralization and Biodemineralization. Met Ions Life Sci. 2010;4:413-456. [PubMed] [Cited in This Article: ] |
| 49. | Mafe? S, Manzanares JA, Reiss H, Thomann JM, Gramain P. Model for the dissolution of calcium hydroxyapatite powder. J Phys Chem. 1992;96:861-866. [DOI] [Cited in This Article: ] [Cited by in Crossref: 35] [Cited by in F6Publishing: 35] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 50. | Gasser P, Voegel JC, Gramain P. Surface reactions on hydroxyapatite in the presence of fluoride ions. 1. Saturated and congruent conditions. Colloids Surf A. 1993;74:275-286. [DOI] [Cited in This Article: ] [Cited by in Crossref: 16] [Cited by in F6Publishing: 11] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 51. | Thomann JM, Voegel JC, Gramain P. Quantitative model for the dissolution of calcium hydroxyapatite with a permselective ionic interface. J Coll Interf Sci. 1993;157:369-374. [DOI] [Cited in This Article: ] [Cited by in Crossref: 19] [Cited by in F6Publishing: 19] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 52. | Gasser P, Haikel Y, Voegel JC, Gramain P. Surface reactions of hydroxyapatite in the presence of fluoride ions. 2. Effects of calcium and phosphate in saturated solutions. Colloids Surf A. 1994;88:157-168. [DOI] [Cited in This Article: ] [Cited by in Crossref: 8] [Cited by in F6Publishing: 7] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 53. | Schaad P, Poumier F, Voegel JC, Gramain P. Analysis of calcium hydroxyapatite dissolution in non-stoichiometric solutions. Colloids Surf A. 1997;121:217-228. [DOI] [Cited in This Article: ] [Cited by in Crossref: 11] [Cited by in F6Publishing: 11] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 54. | Pan HB, Darvell BW. Calcium phosphate solubility: the need for re-evaluation. Cryst Growth Des. 2009;9:639-645. [DOI] [Cited in This Article: ] |
| 55. | Christoffersen J, Christoffersen MR, Kjaergaard N. The kinetics of dissolution of calcium hydroxyapatite in water at constant pH. J Cryst Growth. 1978;43:501-511. [DOI] [Cited in This Article: ] |
| 56. | Christoffersen J. Kinetics of dissolution of calcium hydroxypatite. III. Nucleation-controlled dissolution of a polydisperse sample of crystals. J Cryst Growth. 1980;49:29-44. [DOI] [Cited in This Article: ] |
| 57. | Christoffersen J. Dissolution of calcium hydroxyapatite. Calcif Tissue Int. 1981;33:557-560. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 17] [Cited by in F6Publishing: 17] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 58. | Christoffersen J, Christoffersen MR. Kinetics of dissolution of calcium hydroxyapatite. V. The acidity constant for the hydrogen phosphate surface complex. J Cryst Growth. 1982;57:21-26. [DOI] [Cited in This Article: ] |
| 59. | Christoffersen MR, Christoffersen J. Possible mechanisms for the growth of the biomaterial, calcium hydroxyapatite microcrystals. J Cryst Growth. 1992;121; 617-630. [DOI] [Cited in This Article: ] |
| 60. | Christoffersen J, Christoffersen MR, Johansen T. Kinetics of growth and dissolution of fluorapatite. J Cryst Growth. 1996;163:295-303. [DOI] [Cited in This Article: ] |
| 61. | Christoffersen J, Christoffersen MR, Johansen T. Some new aspects of surface nucleation applied to the growth and dissolution of fluorapatite and hydroxyapatite. J Cryst Growth. 1996;163:304-310. [DOI] [Cited in This Article: ] |
| 62. | Christoffersen J, Dohrup J, Christoffersen MR. The importance of formation of hydroxyl ions by dissociation of trapped water molecules for growth of calcium hydroxyapatite crystals. J Cryst Growth. 1998;186:275-282. [DOI] [Cited in This Article: ] |
| 63. | Christoffersen MR, Dohrup J, Christoffersen J. Kinetics of growth and dissolution of calcium hydroxyapatite in suspensions with variable calcium to phosphate ratio. J Cryst Growth. 1998;186:283-290. [DOI] [Cited in This Article: ] |
| 64. | Zhang H, Li S, Yan Y. Dissolution behavior of hydroxyapatite powder in hydrothermal solution. Ceram Int. 2001;27:451-454. [DOI] [Cited in This Article: ] |
| 65. | Gilmer GH, Bennema P. Simulation of crystal growth with surface diffusion. J Appl Physics. 1972;43:1347-1360. [DOI] [Cited in This Article: ] |
| 66. | Onuma K, Ito A, Tateishi T, Kameyama T. Growth kinetics of hydroxyapatite crystal revealed by atomic force microscopy. J Cryst Growth. 1995;154:118-125. [DOI] [Cited in This Article: ] |
| 67. | Onuma K, Ito A, Tateishi T. Investigation of a growth unit of hydroxyapatite crystal from the measurements of step kinetics. J Cryst Growth. 1996;167:773-776. [DOI] [Cited in This Article: ] |
| 68. | Zhu Y, Zhang X, Chen Y, Xie Q, Lan J, Qian M, He N. A comparative study on the dissolution and solubility of hydroxylapatite and fluorapatite at 25°C and 45°C. Chemical Geology. 2009;268:89-96. [DOI] [Cited in This Article: ] |
| 69. | Kukura M, Bell LC, Posner AM, Quirk JP. Radioisotope determination of the surface concentrations of calcium and phosphorus on hydroxyapatite in aqueous solution. J Phys Chem. 1972;76:900-904. [DOI] [Cited in This Article: ] [Cited by in Crossref: 61] [Cited by in F6Publishing: 61] [Article Influence: 2.8] [Reference Citation Analysis (0)] |
| 70. | Somasundaran P. Zeta potential of apatite in aqueous solutions and its change during equilibration. J Coll Interf Sci. 1968;27:659-666. [DOI] [Cited in This Article: ] [Cited by in Crossref: 157] [Cited by in F6Publishing: 156] [Article Influence: 2.8] [Reference Citation Analysis (0)] |
| 71. | Bell LC, Posner AM, Quirk JP. Surface charge characteristics of hydroxyapatite and fluorapatite. Nature. 1972;239:515-517. [DOI] [Cited in This Article: ] [Cited by in Crossref: 33] [Cited by in F6Publishing: 33] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 72. | Bell LC, Posner AM, Quirk JP. The point of zero charge of hydroxyapatite and fluorapatite in aqueous solutions. J Coll Interf Sci. 1973;42:250-261. [DOI] [Cited in This Article: ] [Cited by in Crossref: 153] [Cited by in F6Publishing: 122] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 73. | Moreno EC, Gregory TM, Brown WE. Preparation and solubility of hydroxyapatite. J Res Natl Bur Stand. 1968;72A:773-782. [Cited in This Article: ] |
| 74. | Chuong R. Experimental study of surface and lattice effects on the solubility of hydroxyapatite. J Dent Res. 1973;52:911-914. [DOI] [Cited in This Article: ] [Cited by in Crossref: 34] [Cited by in F6Publishing: 36] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 75. | Smith AN, Posner AM, Quirk JP. Incongruent dissolution and surface complexes of hydroxyapatite. J Coll Interf Sci. 1974;48:442-449. [DOI] [Cited in This Article: ] [Cited by in Crossref: 37] [Cited by in F6Publishing: 30] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 76. | Mika H, Bell LC, Kruger BJ. The role of surface reactions in the dissolution of stoichiometric hydroxyapatite. Arch Oral Biol. 1976;21:697-701. [DOI] [Cited in This Article: ] [Cited by in Crossref: 22] [Cited by in F6Publishing: 22] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 77. | Moreno EC, Kresak M, Zahradnik RT. Physicochemical aspects of fluoride-apatite systems relevant to the study of dental caries. Caries Res. 1977;11 Suppl 1:142-171. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 193] [Cited by in F6Publishing: 197] [Article Influence: 4.2] [Reference Citation Analysis (0)] |
| 78. | Bell LC, Mika H, Kruger BJ. Synthetic hydroxyapatite-solubility product and stoichiometry of dissolution. Arch Oral Biol. 1978;23:329-336. [DOI] [Cited in This Article: ] [Cited by in Crossref: 67] [Cited by in F6Publishing: 67] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 79. | Larsen MJ. Chemical events during tooth dissolution. J Dent Res. 1990;69 Spec No:575-580; discussion 634-636. [PubMed] [Cited in This Article: ] |
| 80. | Kaufman HW, Kleinberg I. Studies on the incongruent solubility of hydroxyapatite. Calcif Tissue Int. 1979;27:143-151. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 27] [Cited by in F6Publishing: 27] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 81. | Amrah-Bouali S, Rey C, Lebugle A, Bernache D. Surface modifications of hydroxyapatite ceramics in aqueous media. Biomaterials. 1994;15:269-272. [DOI] [Cited in This Article: ] [Cited by in Crossref: 40] [Cited by in F6Publishing: 41] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 82. | Nordström EG, Hara T, Herø H. Solubility of hydroxyapatite/mica composites. Biomed Mater Eng. 1996;6:73-78. [PubMed] [Cited in This Article: ] |
| 83. | Pearce EI, Guha-Chowdhury N, Iwami Y, Cutress TW. Stoichiometry of fluoride release from fluorhydroxyapatite during acid dissolution. Caries Res. 1995;29:130-136. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 8] [Cited by in F6Publishing: 8] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 84. | Shimabayashi S, Matsumoto M. Non-stoichiometric dissolution of hydroxyapatite in the presence of simple salts. Nippon Kagaku Kaishi. 1993;10:1118-1122. [DOI] [Cited in This Article: ] [Cited by in Crossref: 7] [Cited by in F6Publishing: 7] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 85. | Brown PW, Martin RI. An analysis of hydroxyapatite surface layer formation. J Phys Chem B. 1999;103:1671-1675. [DOI] [Cited in This Article: ] [Cited by in Crossref: 66] [Cited by in F6Publishing: 66] [Article Influence: 2.6] [Reference Citation Analysis (0)] |
| 86. | Chaïrat C, Oelkers EH, Schott J, Lartigue JE. Fluorapatite surface composition in aqueous solution deduced from potentiometric, electrokinetic, and solubility measurements, and spectroscopic observations. Geochim Cosmochim Acta. 2007;71:5888-5900. [DOI] [Cited in This Article: ] |
| 87. | Bengtsson Å, Shchukarev A, Persson P, Sjöberg S. A solubility and surface complexation study of a non-stoichiometric hydroxyapatite. Geochim Cosmochim Acta. 2009;73:257-267. [DOI] [Cited in This Article: ] |
| 88. | Bengtsson Å, Shchukarev A, Persson P, Sjöberg S. Phase transformations, ion-exchange, adsorption, and dissolution processes in aquatic fluorapatite systems. Langmuir. 2009;25:2355-2362. [PubMed] [DOI] [Cited in This Article: ] |
| 89. | Bengtsson Å, Sjöberg S. Surface complexation and proton-promoted dissolution in aqueous apatite systems. Pure Appl Chem. 2009;81:1569-1584. [DOI] [Cited in This Article: ] [Cited by in Crossref: 29] [Cited by in F6Publishing: 29] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 90. | Feng MH, Ngwenya BT, Wang L, Li W, Olive V, Ellam RM. Bacterial dissolution of fluorapatite as a possible source of elevated dissolved phosphate in the environment. Geochim Cosmochim Acta. 2011;75:5785-5796. [DOI] [Cited in This Article: ] |
| 91. | Misra DN. Interaction of citric or hydrochloric acid with calcium fluorapatite: precipitation of calcium fluoride. J Coll Interf Sci. 1999;220:387-391. [DOI] [Cited in This Article: ] [Cited by in Crossref: 8] [Cited by in F6Publishing: 8] [Article Influence: 0.3] [Reference Citation Analysis (0)] |
| 92. | Dobrydnev SV, Bogach VV, Beskov VS. Thermodynamic grounds of sulfuric acid dissolution of fluorapatite. Russ J Inorg Chem. 2002;47:1063-1066. [Cited in This Article: ] |
| 93. | Dobrydnev SV, Bogach VV, Beskov VS. Thermodynamics of fluoroapatite dissolution in phosphoric acid. Russ J Inorg Chem. 2002;47:1214-1216. [Cited in This Article: ] |
| 94. | Dobrydnev SV, Bogach VV, Beskov VS. Thermodynamics of fluoroapatite dissolution in nitric acid. Russ J Inorg Chem. 2002;47:1217-1220. [Cited in This Article: ] |
| 95. | Harouiya N, Chaïrat C, Köhler SJ, Gout R, Oelkers EH. The dissolution kinetics and apparent solubility of natural apatite in closed reactors at temperatures from 5 to 50°C and pH from 1 to 6. Chemical Geology. 2007;244:554-568. [DOI] [Cited in This Article: ] |
| 96. | Chaïrat C, Schott J, Oelkers EH, Lartigue JE, Harouiya N. Kinetics and mechanism of natural fluorapatite dissolution at 25°C and pH from 3 to 12. Geochim Cosmochim Acta. 2007;71:5901-5912. [DOI] [Cited in This Article: ] |
| 97. | Melikhov IV, Dorozhkin SV, Nikolaev AL, Voronina NY. Transition from congruent to incongruent dissolution. Russ J Phys Chem. 1992;66:1108-1111. [Cited in This Article: ] |
| 98. | Tanaka H, Miyajima K, Nakagaki M, Shimabayashi S. Incongruent dissolution of hydroxyapatite in the presence of phosphoserine. Coll Polymer Sci. 1991;269:161-165. [DOI] [Cited in This Article: ] [Cited by in Crossref: 6] [Cited by in F6Publishing: 5] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 99. | Park C, Fenter P, Zhang Z, Cheng L, Sturchio NC. Structure of the fluorapatite (100)-water interface by high-resolution X-ray reflectivity. Am Mineral. 2004;89:1647-1654. [Cited in This Article: ] |
| 100. | Dorozhkin SV. Surface Reactions of Apatite Dissolution. J Colloid Interface Sci. 1997;191:489-497. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 85] [Cited by in F6Publishing: 87] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 101. | Dorozhkin SV. Acidic dissolution mechanism of natural fluorapatite. II. Nanolevel of investigations. J Cryst Growth. 1997;182:133-140. [DOI] [Cited in This Article: ] |
| 102. | Dorozhkin SV. Inorganic chemistry of the dissolution phenomenon: the dissolution mechanism of calcium apatites at the atomic (ionic) level. Comments Inorg Chem. 1999;20:285-299. [DOI] [Cited in This Article: ] [Cited by in Crossref: 42] [Cited by in F6Publishing: 27] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 103. | Higuchi WI, Gray JA, Hefferren JJ, Patel PR. Mechanisms of enamel dissolution in acid buffers. J Dent Res. 1965;44:330-341. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 51] [Cited by in F6Publishing: 52] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 104. | Pearce EI. On the dissolution of hydroxyapatite in acid solutions. J Dent Res. 1988;67:1056-1059. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 18] [Cited by in F6Publishing: 18] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 105. | Eanes ED, Meyer JL. The maturation of crystalline calcium phosphates in aqueous suspensions at physiologic pH. Calcif Tissue Res. 1977;23:259-269. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 177] [Cited by in F6Publishing: 183] [Article Influence: 3.9] [Reference Citation Analysis (0)] |
| 106. | Lowell LC. Dislocation etch pits in apatite. Acta Metall. 1958;6:775-778. [DOI] [Cited in This Article: ] [Cited by in Crossref: 29] [Cited by in F6Publishing: 29] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 107. | Jongebloed WL, Molenaar I, Arends J. Orientation-dependent etchpit penetration and dissolution of fluoroapatite. Caries Res. 1973;7:154-165. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 23] [Cited by in F6Publishing: 23] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 108. | Jongebloed WL, van den Berg PJ, Arends J. The dissolution of single crystals of hydroxyapatite in citric and lactic acids. Calcif Tissue Res. 1974;15:1-9. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 46] [Cited by in F6Publishing: 47] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 109. | Arends J, Jongebloed WL. Dislocations and dissolution in apatites: theoretical considerations. Caries Res. 1977;11:186-188. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 41] [Cited by in F6Publishing: 42] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 110. | Arends J, Jongebloed WL. Ultrastructural studies of synthetic apatite crystals. J Dent Res. 1979;58:837-843. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 21] [Cited by in F6Publishing: 21] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 111. | Daculsi G, Kerebel B, Kerebel LM. Mechanisms of acid dissolution of biological and synthetic apatite crystals at the lattice pattern level. Caries Res. 1979;13:277-289. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 25] [Cited by in F6Publishing: 26] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 112. | Daculsi G, LeGeros RZ, Mitre D. Crystal dissolution of biological and ceramic apatites. Calcif Tissue Int. 1989;45:95-103. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 123] [Cited by in F6Publishing: 126] [Article Influence: 3.6] [Reference Citation Analysis (0)] |
| 113. | Melikhov IV, Dorozhkin SV, Nikolaev AL, Kozlovskaya ED, Rudin VN. Dislocations and the rate of dissolution of solids. Russ J Phys Chem. 1990;64:1746-1750. [Cited in This Article: ] |
| 114. | Dorozhkin SV. Chemical etching of natural fluorapatite crystals in acid solutions studied with the scanning electron microscope. Scanning. 1995;17:355-360. [DOI] [Cited in This Article: ] |
| 115. | Dorozhkin SV. Acidic dissolution mechanism of natural fluorapatite. I. Milli- and microlevels of investigations. J Cryst Growth. 1997;182:125-132. [DOI] [Cited in This Article: ] |
| 116. | Lasaga AC, Luttge A. Variation of crystal dissolution rate based on a dissolution stepwave model. Science. 2001;291:2400-2404. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 339] [Cited by in F6Publishing: 95] [Article Influence: 4.1] [Reference Citation Analysis (0)] |
| 117. | Dove PM, Han N, De Yoreo JJ. Mechanisms of classical crystal growth theory explain quartz and silicate dissolution behavior. Proc Natl Acad Sci USA. 2005;102:15357-15362. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 215] [Cited by in F6Publishing: 76] [Article Influence: 4.0] [Reference Citation Analysis (0)] |
| 118. | Kwon KY, Wang E, Chung A, Chang N, Saiz E, Choe UJ, Koobatian M, Lee SW. Defect induced asymmetric pit formation on hydroxyapatite. Langmuir. 2008;24:11063-11066. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 26] [Cited by in F6Publishing: 9] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 119. | Kwon KY, Wang E, Chung A, Chang N, Lee SW. Effect of salinity on hydroxyapatite dissolution studied by atomic force microscopy. J Phys Chem C. 2009;113; 3369-3372. [DOI] [Cited in This Article: ] |
| 120. | Kwon KY, Wang E, Chang N, Lee SW. Characterization of the dominant molecular step orientations on hydroxyapatite (100) surfaces. Langmuir. 2009;25:7205-7208. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 23] [Cited by in F6Publishing: 14] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 121. | Kwon KY, Wang E, Nofal M, Lee SW. Microscopic study of hydroxyapatite dissolution as affected by fluoride ions. Langmuir. 2011;27:5335-5339. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 18] [Cited by in F6Publishing: 7] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 122. | Dong SS, Hwan K, Jong KL. AFM study on the surface dissolution of hydroxyapatite. Key Eng Mater. 2007;336-338:1553-1555. [DOI] [Cited in This Article: ] [Cited by in Crossref: 2] [Cited by in F6Publishing: 2] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 123. | Wang LJ, Lu JW, Xu FS, Zhang FS. Dynamics of crystallization and dissolution of calcium orthophosphates at the near-molecular level. Chinese Sci Bull. 2011;56:713-721. [DOI] [Cited in This Article: ] [Cited by in Crossref: 18] [Cited by in F6Publishing: 15] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 124. | Dorozhkin SV. Process of epitaxial crystal growth for CaSO4•0.5H2O on a surface of dissolving fluorapatite crystals studied by scanning electron microscopy. Scanning. 1996;18:119-124. [DOI] [Cited in This Article: ] |
| 125. | Misra DN. Interaction of citric acid with hydroxyapatite: surface exchange of ions and precipitation of calcium citrate. J Dent Res. 1996;75:1418-1425. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 53] [Cited by in F6Publishing: 53] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 126. | Lo?pez-Macipe A, Go?mez-Morales J, Rodri?guez-Clemente R. The role of pH in the adsorption of citrate ions on hydroxyapatite. J Coll Interf Sci. 1998;200:114-120. [DOI] [Cited in This Article: ] [Cited by in Crossref: 83] [Cited by in F6Publishing: 83] [Article Influence: 3.2] [Reference Citation Analysis (0)] |
| 127. | Misra DN. Adsorption from solutions on synthetic hydroxyapatite: nonaqueous vs. aqueous solvents. J Biomed Mater Res. 1999;48:848-855. [PubMed] [DOI] [Cited in This Article: ] [Cited by in F6Publishing: 1] [Reference Citation Analysis (0)] |
| 128. | Filgueiras MRT, Mkhonto D, de Leeuw NH. Computer simulations of the adsorption of citric acid at hydroxyapatite surfaces. J Cryst Growth. 2006;294; 60-68. [DOI] [Cited in This Article: ] |
| 129. | Jiang W, Pan H, Cai Y, Tao J, Liu P, Xu X, Tang R. Atomic force microscopy reveals hydroxyapatite-citrate interfacial structure at the atomic level. Langmuir. 2008;24:12446-12451. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 52] [Cited by in F6Publishing: 29] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 130. | Yoshida Y, Van Meerbeek B, Nakayama Y, Yoshioka M, Snauwaert J, Abe Y, Lambrechts P, Vanherle G, Okazaki M. Adhesion to and decalcification of hydroxyapatite by carboxylic acids. J Dent Res. 2001;80:1565-1569. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 199] [Cited by in F6Publishing: 200] [Article Influence: 8.7] [Reference Citation Analysis (0)] |
| 131. | Yoshioka M, Yoshida Y, Inoue S, Lambrechts P, Vanherle G, Nomura Y, Okazaki M, Shintani H, Van Meerbeek B. Adhesion/decalcification mechanisms of acid interactions with human hard tissues. J Biomed Mater Res. 2002;59:56-62. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 148] [Cited by in F6Publishing: 150] [Article Influence: 6.8] [Reference Citation Analysis (0)] |
| 132. | Yoshida Y, Van Meerbeek B, Nakayama Y, Snauwaert J, Hellemans L, Lambrechts P, Vanherle G, Wakasa K. Evidence of chemical bonding at biomaterial-hard tissue interfaces. J Dent Res. 2000;79:709-714. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 305] [Cited by in F6Publishing: 311] [Article Influence: 13.0] [Reference Citation Analysis (0)] |
| 133. | Astala R, Stott MJ. First-principles study of hydroxyapatite surfaces and water adsorption. Phys Rev B. 2008;78:075427 (11 pages). [DOI] [Cited in This Article: ] |
| 134. | Posner AS. The structure of bone apatite surfaces. J Biomed Mater Res. 1985;19:241-250. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 55] [Cited by in F6Publishing: 56] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 135. | Hochrein O, Zahn D. On the molecular mechanisms of the acid-induced dissociation of hydroxy-apatite in water. J Mol Model. 2011;17:1525-1528. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 12] [Cited by in F6Publishing: 11] [Article Influence: 0.8] [Reference Citation Analysis (0)] |
| 136. | Jarlbring M, Gunneriusson L, Forsling W. Characterisation of the protolytic properties of synthetic carbonate free fluorapatite. J Colloid Interface Sci. 2005;285:206-211. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 9] [Cited by in F6Publishing: 9] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 137. | Becker P. Phosphates and phosphoric acid: raw materials technology and economics of the wet process. 2nd Ed. Fertilizer science and technology series. New York, USA: Marcel Dekker 1989; 760 pp. [Cited in This Article: ] |
| 138. | Compton RG, Harding MS, Pluck MR, Atherton JH, Brennan CM. Mechanism of solid/liquid interfacial reactions. The dissolution of benzoic acid in aqueous solution. J Phys Chem. 1993;97:10416-10420. [DOI] [Cited in This Article: ] [Cited by in Crossref: 27] [Cited by in F6Publishing: 27] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 139. | Zhang J, Nancollas GH. Unexpected pH dependence of dissolution kinetics of dicalcium phosphate dihydrate. J Phys Chem. 1994;98:1689-1694. [DOI] [Cited in This Article: ] [Cited by in Crossref: 12] [Cited by in F6Publishing: 12] [Article Influence: 0.5] [Reference Citation Analysis (0)] |
| 140. | de Aza PN, Guitian F, Merlos A, Lora-Tamayo E, de Aza S. Bioceramics – simulated body fluid interfaces: pH and its influence of hydroxyapatite formation. J Mater Sci Mater Med. 1996;7:399-402. [DOI] [Cited in This Article: ] |
| 141. | Bohner M, Lemaître J, Ring TA. Kinetics of Dissolution of beta-Tricalcium Phosphate. J Colloid Interface Sci. 1997;190:37-48. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 37] [Cited by in F6Publishing: 38] [Article Influence: 1.4] [Reference Citation Analysis (0)] |
| 142. | Young RA. Implications of atomic substitutions and other structural details in apatites. J Dent Res. 1974;53:193-203. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 117] [Cited by in F6Publishing: 115] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 143. | de Leeuw NH. Computer simulations of structures and properties of the biomaterial hydroxyapatite. J Mater Chem. 2010;20:5376-5389. [DOI] [Cited in This Article: ] [Cited by in Crossref: 58] [Cited by in F6Publishing: 59] [Article Influence: 4.2] [Reference Citation Analysis (0)] |
| 144. | Pareek A, Torrelles X, Angermund K, Rius J, Magdans U, Gies H. Structure of interfacial water on fluorapatite (100) surface. Langmuir. 2008;24:2459-2464. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 24] [Cited by in F6Publishing: 10] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 145. | Pan H, Tao J, Wu T, Tang R. Molecular simulation of water behaviors on crystal faces of hydroxyapatite. Zhongguo Huaxve Qianyan. 2007;2:156-163. [DOI] [Cited in This Article: ] [Cited by in Crossref: 22] [Cited by in F6Publishing: 17] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 146. | Zahn D, Hochrein O. Computational study of interfaces between hydroxyapatite and water. Phys Chem Chem Phys. 2003;5:4004-4007. [DOI] [Cited in This Article: ] [Cited by in Crossref: 89] [Cited by in F6Publishing: 89] [Article Influence: 4.2] [Reference Citation Analysis (0)] |
| 147. | Corno M, Busco C, Bolis V, Tosoni S, Ugliengo P. Water adsorption on the stoichiometric (001) and (010) surfaces of hydroxyapatite: a periodic B3LYP study. Langmuir. 2009;25:2188-2198. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 74] [Cited by in F6Publishing: 37] [Article Influence: 2.5] [Reference Citation Analysis (0)] |
| 148. | Pareek A, Torrelles X, Rius J, Magdans U, Gies H. Role of water in the surface relaxation of the fluorapatite (100) surface by grazing incidence X-ray diffraction. Phys Rev B. 2007;75:035418 (6 pages). [DOI] [Cited in This Article: ] |
| 149. | Pan H, Tao J, Yu X, Fu L, Zhang J, Zeng X, Xu G, Tang R. Anisotropic demineralization and oriented assembly of hydroxyapatite crystals in enamel: smart structures of biominerals. J Phys Chem B. 2008;112:7162-7165. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 22] [Cited by in F6Publishing: 24] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 150. | Dorozhkin SV. Nanodimensional and nanocrystalline apatites and other calcium orthophosphates in biomedical engineering, biology and medicine. Materials. 2009;2:1975-2045. [DOI] [Cited in This Article: ] [Cited by in Crossref: 192] [Cited by in F6Publishing: 194] [Article Influence: 12.9] [Reference Citation Analysis (0)] |
| 151. | Dorozhkin SV. Nanosized and nanocrystalline calcium orthophosphates. Acta Biomater. 2010;6:715-734. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 386] [Cited by in F6Publishing: 239] [Article Influence: 17.1] [Reference Citation Analysis (0)] |
| 152. | Probstein RF. Physicochemical hydrodynamics: an introduction. 2nd ed. Hoboken, NJ, USA: Wiley 2003; 416 pp. [Cited in This Article: ] |
| 153. | Wu L, Forsling W, Schindler PW. Surface complexation of calcium minerals in aqueous solution. 1. Surface protonation at fluorapatite-water interfaces. J Coll Interf Sci. 1991;147:178-185. [DOI] [Cited in This Article: ] [Cited by in Crossref: 166] [Cited by in F6Publishing: 166] [Article Influence: 5.0] [Reference Citation Analysis (0)] |
| 154. | Skartsila K, Spanos N. Surface characterization of hydroxyapatite: potentiometric titrations coupled with solubility measurements. J Colloid Interface Sci. 2007;308:405-412. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 42] [Cited by in F6Publishing: 43] [Article Influence: 2.5] [Reference Citation Analysis (0)] |
| 155. | Vucinić DR, Radulović DS, Deusić SD. Electrokinetic properties of hydroxyapatite under flotation conditions. J Colloid Interface Sci. 2010;343:239-245. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 45] [Cited by in F6Publishing: 46] [Article Influence: 3.1] [Reference Citation Analysis (0)] |
| 156. | Zhang J, Nancollas GH. Kinetics and mechanisms of octacalcium phosphate dissolution at 37°C. J Phys Chem. 1992;96:5478-5483. [DOI] [Cited in This Article: ] [Cited by in Crossref: 42] [Cited by in F6Publishing: 42] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 157. | Doss SK. Surface properties of hydroxyapatite: I. The effect of various inorganic ions on the electrophoretic behavior. J Dent Res. 1976;55:1067-1075. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 29] [Cited by in F6Publishing: 29] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 158. | Dobrydnev SV, Bogach VV, Beskov VS. Influence of surfactants on the rate of decomposition of apatites by mineral acids. Theoret Found Chem Eng. 2003;37:412-415. [DOI] [Cited in This Article: ] |
| 159. | Nielsen AE. Transport control in crystal growth from solution. Croat Chem Acta. 1980;53:255-279. [Cited in This Article: ] |
| 160. | Okazaki M, Sato M, Takahashi J. Space-cutting model of hydroxyapatite. Biomaterials. 1995;16:45-49. [DOI] [Cited in This Article: ] [Cited by in Crossref: 4] [Cited by in F6Publishing: 5] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 161. | Iijima M, Nelson DG, Pan Y, Kreinbrink AT, Adachi M, Goto T, Moriwaki Y. Fluoride analysis of apatite crystals with a central planar OCP inclusion: concerning the role of F- ions on apatite/OCP/apatite structure formation. Calcif Tissue Int. 1996;59:377-384. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 42] [Cited by in F6Publishing: 41] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 162. | Aoba T. The effect of fluoride on apatite structure and growth. Crit Rev Oral Biol Med. 1997;8:136-153. [DOI] [Cited in This Article: ] [Cited by in Crossref: 128] [Cited by in F6Publishing: 99] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 163. | de Leeuw NH. Resisting the onset of hydroxyapatite dissolution through the incorporation of fluoride. J Phys Chem B. 2004;108:1809-1811. [DOI] [Cited in This Article: ] [Cited by in Crossref: 81] [Cited by in F6Publishing: 80] [Article Influence: 4.0] [Reference Citation Analysis (0)] |
| 164. | Liu Y, Sethuraman G, Wu W, Nancollas GH, Grynpas M. The Crystallization of Fluorapatite in the Presence of Hydroxyapatite Seeds and of Hydroxyapatite in the Presence of Fluorapatite Seeds. J Colloid Interface Sci. 1997;186:102-109. [PubMed] [DOI] [Cited in This Article: ] [Cited by in Crossref: 23] [Cited by in F6Publishing: 25] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 165. | Dickens B, Schroeder LW. Investigation of epitaxy relationships between Ca5(PO4)3OH and other calcium orthophosphates. J Res Natl Bur Stand. 1980;85:347-362. [Cited in This Article: ] |
| 166. | Kaischew R. Zur Theorie des Kristallwachstums. Zeitschrift für Physik. 1936;102:684-690. [DOI] [Cited in This Article: ] |
| 167. | Nangia S, Garrison BJ. Ab initio study of dissolution and precipitation reactions from the edge, kink, and terrace sites of quartz as a function of pH. Molecular Phys. 2009;107:831-843. [DOI] [Cited in This Article: ] [Cited by in Crossref: 27] [Cited by in F6Publishing: 23] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 168. | Kossel W. Zur Energetik von Oberflächenvorgangen. Annalen der Physik. 1934;21:457-480. [DOI] [Cited in This Article: ] |